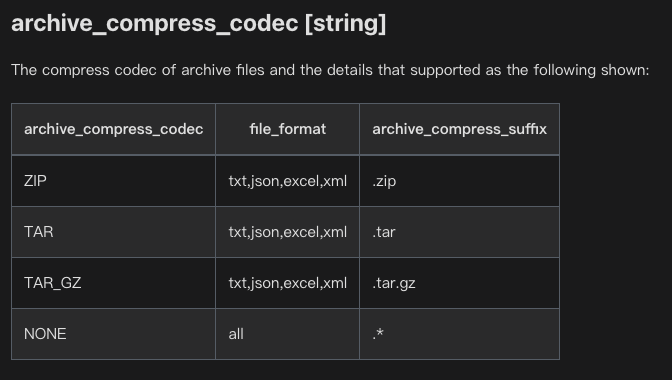
雷达系统中杂波信号的建模与仿真
2 杂波建模与模拟方法
2.1 杂波建模
杂波可以说是雷达在所处环境中接收到的不感兴趣的回波[4]。就像目标回波一样,杂波也是极为复杂的。为了有效地克服杂波对信号检测的影响,需要知道杂波的幅度特性以及频谱特性。除独立的建筑物、岩石等可以认为是固定目标外,大多数地物、海浪杂波都是极为复杂的,它可能既包含有固定的部分又包含有运动的部分,而每一部分反射回来的回波,其振幅和相位都是随机的[5]。通常采用一些比较接近而又合理的数学模型来表示杂波幅度的概率分布特性,这就是雷达杂波模型。目前描述杂波模型主要有三种方式:
(1)描述杂波散射单元机理的机理模型;
(2)描述杂波后向散射系数的概率密度函数的分布模型;
(3)描述由实验数据拟合与频率、极化、俯角、环境参数等物理量的依赖关系的关系模型。
2.1.1 雷达杂波幅度分布模型
到目前为止,人们已经提出了许多杂波模型,有关描述杂波后向散射系数的概率密度函数的分布模型,比较公认的幅度概率密度函数分布模型为Rayleigh分布、LogNormal、Weibull分布、K分布等。
(1) Rayleigh(瑞利)分布
在雷达可分辨范围内,当散射体的数目很多的时候,根据散射体反射信号振幅和相位的随机特性,它们合成的回波包络振幅是服从瑞利分布的[6]。以x表示杂波回波的包络振幅,以σ2表示它的功率,则x的概率密度函数为:

(2-1)
相对应的概率密度函数分布曲线如图2.1所示。

图2.1 瑞利分布概率密度函数分布曲线图
瑞利分布与每个散射体的振幅分布无关,只要求散射体的数目足够多,并且所有散射体中没有一个起主导作用。需要说明的是,瑞利分布只能代表同一个距离单元上杂波从这次扫描到下次扫描的变化规律,它不能用来表示同一个扫描过程中杂波回波的振幅分布,因为杂波的强度一般都是随着距离的增大而减弱的。对于低分辨力雷达,当高仰角和平稳环境时,瑞利分布的杂波模型可以得到较为精确的结果。但是,随着对雷达杂波分布特性分析的逐步深入,人们发现,对于海浪杂波和地物杂波,瑞利分布模型并不能给出令人满意的结果。特别是随着距离分辨力的提高,杂波分布出现了比瑞利分布更长的“尾巴”,即出现高振幅的概率相当大。因而,如果继续采用瑞利分布模型,将出现较高的虚警概率。海浪杂波的分布不仅是脉冲宽度的函数,而且也与雷达极化方式、工作频率、天线视角以及海情、风向和风速等因素有关,地物杂波也受类似因素的影响。对于高分辨力雷达,在低仰角或恶劣海情下,海浪杂波己不服从瑞利分布,而通常能用韦布尔分布来描述。类似地,地物杂波通常能用LogNormal分布来描述[7]。
(2) LogNormal(对数一正态)分布
设x代表杂波回波的包络分布,则x的LogNormal分布是:

(2-2)
其中σ代表lnx的标准差,xw是x的中值。
相对应的概率密度函数分布曲线如图2.2所示:

图2.2 LogNormal分布概率密度函数分布曲线图
LogNormal分布的严重缺点是在最影响虚警和灵敏度的区域里,吻合程度反而较差。对数一正态分布和瑞利分布之间的主要差别在于前者的“尾巴”较长,也就是说,大幅度的概率要比后者大一些。
(3) Weibull(韦布尔)分布
一般来说,对于大多数试验和理论所确定的杂波幅度分布,瑞利分布模型和对数一正态分布模型仅适用于它们中的有限分布。瑞利分布模型一般地倾向于低估实际杂波分布的动态范围,而对数一正态分布倾向于高估实际杂波分布的动态范围[8]。韦布尔杂波分布模型比瑞利分布模型、对数一正态杂波分布模型常常能在更广的环境内精确的表示实际的杂波分布。适当地调整韦布尔分布的参数,能够使它成为瑞利分布或接近于对数一正态分布。通常,在使用高分辨力雷达,低入射角的情况下,海浪杂波能够用韦布尔分布模型精确地描述,地物杂波也能够用韦布尔分布模型描述。
设x代表杂波回波的包络振幅,则x的韦布尔分布为:
(2-3)
其中:xm为尺度参数,是分布的中值;a为分布的形状(斜度)函数。
相对应的概率密度函数分布曲线如图2.3所示:
图2.3 Weibull分布概率密度函数分布曲线图
如果把式(2-3 )形状参数a固定为2,并把改写成2σ2,则式(2-3 )变为:
(2-4)
这就是瑞利分布。
所以,瑞利分布是韦布尔分布的特例。
如果a=1,并把改写成2σ2,则韦布尔分布变为:
(2-5)
这就是指数分布。从信号检测的观点来说,对数一正态分布代表着最恶劣的杂波环境:瑞利分布代表最简单的杂波环境;韦布尔分布是中间模型[9]。在许多情况下,它是一种比较合适的杂波模型,因此,它比瑞利分布能适应更宽的杂波范围。
(4)K分布:
它的表达式如下:
(2-6)
其中x为幅度,a为量化参数,v为形状参数,它的取值范围为一1<v<∞,
它的变化决定了杂波分布的特征。Kv为修正贝塞耳(Bessel)函数。
相对应的概率密度函数分布曲线如图2.4所示:
图2.4 K分布概率密度函数分布曲线图
对于高精度雷达来说,K分布是比较符合杂波数据的统计结果的。实际上,可以把K分布看作是瑞利分布和x2分布的组合:快速起伏的杂波,服从瑞利分布;慢速起伏的杂波,服从x2分布。
雷达杂波幅度的概率密度分布模型描述了杂波信号在时域的一维表示,通常要更好的描述杂波的分布特性,还要描述杂波频域的二维分布特性,这就是杂波的频谱分布模型[10]。
2.1.2 雷达杂波频谱分布模型
雷达杂波的频谱常用以下三种模型表示:
(1) Gaussian(高斯)谱模型: Gaussian谱模型可以表示为
(2-7)
其中σf为杂波谱的标准差。
(2) Cauchy(柯西)谱模型: Cauchy谱模型可以表示为
(2-8)
其中,fc为截止频率,在该频率处信号幅度下降3dB。
(3) AllPole(全极)谱模型: 全极型谱能更好地描述杂波谱的“尾巴”,它的表达式为
(2-9)
式中,fc的意义同柯西谱模型。n的典型值为2~5,当n=2时,全极型谱即为柯西谱,当n=3时,即为通常所说的立方谱。
对于地杂波可采用幅度为瑞利分布、对数一正态分布、韦布尔分布,频谱为高斯型、立方型、指数型的杂波模型[11]。
海杂波可采用幅度为对数一正态分布、韦布尔分布、K分布的高斯杂波模型。
气象杂波和箔条干扰可采用瑞利分布的高斯型杂波模型。
具体对应某种杂波,采用何种幅度分布和频谱模型由实际情况决定。
2.2 相关杂波的模拟方法
2.2.1 相关高斯序列的模拟方法
令x(k△t)和X(n△f)分别是随机过程在时域和频域的复取样,其中△t是时域取样间隔,△f是频域取样间隔。由于离散随机过程采样是独立的,所以对于给定的功率谱序列{S(n△f)},我们就可以通过产生一个独立的随机序列{X(n△f)}的办法来产生随机过程总体,则其总体平均功率为:
(2-10)
产生随机序列的方法是简捷的。首先引入独立随机相位因子序列{ξn},它的各分量均值为零,且其总体平均功率为1,且|{ξn}|2=1。再令
n=0,1,2……Nr 
(2-11)
式(2-11)中,Nr是重复周期长度。它是满足(2-10)式的。
采用这种方法必须注意Nr和△f的选择,因为这里考虑的是在时域和频域都是周期重复的随机过程,必须合理的选择Nr和△f,以避免混叠出现。采样频率△f=1/(Nr. △t)。选择Nr的原则是:
N>=max{N,Nc} (2-12)
式(2-12)中,N是所要产生的杂波过程的长度;Nc是杂波过程的相关长度。
利用IFFT变换就可以得到相关随机序列x(k△t),其过程如图2.5所示。
图2.5相关高斯序列产生原理方框图
图2.5中, 
(2-13)
当且仅当相位因子{ξn}各分量的概率分布是高斯分布时,{x(k△t)}的各分量才是高斯分布。这样便产生了符合特定功率谱要求的相关高斯分布序列。
ZMNL法需要找到高斯序列与所需序列相关系数之间的非线性关系g(.),且它随不同的分布而不同,故不能对协方差矩阵和概率密度函数进行独立控制[12]。
2.2.2 相关对数正态分布杂波的建模
利用已产生的相关高斯随机序列,可得到相关对数正态分布的随机序列,分析如下:对于随机变量y~N(lnu,σ2) ,做线性变换x=exp(y),得到具有两个参数的对数正态分布随机变量X的PDF为:

(2-14)
式(2-14)中,u为比例因子,根据具体的环境而不同。
由于在时域幅度上的变换会对功率谱产生影响,所以图5.4中的H(f)不再是单纯的高斯谱采样,而是要经过非线性补偿。设Si,j为y(n△t)的自相关函数,对应高斯谱Pi,j为经过补偿的功率谱序列{P(n△t)}对应的自相关函数,设其对应的随机序列为w(n△t),则Si,j与Pi,j有对应关系:

(2-15)
其中,形状参数σ决定了非线性变换造成的谐失真程度,Pi,j经过FFT得到经线性补偿的功率谱序列{P(n△t)}。令图2.5中的

(2-16)
则可得到非线性补偿功率谱高斯分布的随机序列{y(n△t)},在经非线性变换x=exp(y),可得高斯谱对数正态分布的随机序列{x(n△t)},此过程如图2.6所示:

图2.6相关对数止态分布序列产生方框图
2.2.3 相关韦布尔分布杂波的建模
韦布尔分布的概率密度函数为:

(2-17)
式(2-17)中:q为比例因子,p为形状因子。若p=2,就成为瑞利分布,若
P=1就是指数概率密度函数。
Si,j, Pi,j的关系为:

(2-18)
式(2-18)中:г(.)为gamma函数,2F1(.)为高斯超几何分布函数。高斯超几何分布函数的定义如下:

(2-19)
由于无法由上式(2-19)解出Pij的表达式,因此无法象对数一正态分布一样直接计算Pij。实际的应用中可以把两者的关系存入一个表中,通过查表法来计算。此模拟过程如图2.7所示

图2.7相关韦布尔分布序列产生方框图
2.2.4 相关K分布杂波的建模
在相关K分布模型中,杂波回波的幅度被描述为两个因子的乘积,第一部分是斑点分量(即快变化分量),它是由大量散射体的反射进行相参叠加而成的,符合瑞利分布,即第二部分是基本幅度调制分量(即慢变化分量),它反映了与大面积结构有关的散射束在空间变化的平均电平,具有长相关时间,服从x分布[13]。
相关K分布的概率密度函数为:

(2-20)
其中,x>0是杂波幅度,г(.)为Gamma函数,Kv(.)为第二类修正的v阶Bessel函数v>一1是形状参数,a是标度参数。形状参数v规定了与平均值有关的较大的矩,并通过混合模型规定了在平均值中的不均匀量;对于大多数杂波,形状参数v的取值范围是0.1<v<∞。对于较小的取值(即v—>0.1)杂波有较长的拖尾,并意味着有尖峰杂波;而当v—>∞时,杂波的分布接近于瑞利分布。
K分布随机序列的n阶矩为:
,则杂波功率为: .
K分布的混合模型包含了杂波起伏的两个部分,它们具有不同的相关时间。第一部分是基本幅度调制分量(即慢变化分量),它是由与散射体结构有关的散射束在空间变化的平均电平所致。它用取平方根的伽马分布表示,并且具有相关性;该相关性依赖于风速等环境条件,有秒量级长的相关时间,且不受频率捷变的影响。这种基本调制分量可通过对数据进行1/4秒的积分而分离出来。
第二部分是斑点分量(即快变化分量),它是由任何距离单元中杂波的多路径散射性质产生的,它是通过散射体内部运动或通过频率捷变而去相关。斑点分量可以从相当短的时间序列的杂波数据中分离出来,这个杂波数据序列时间在单一距离选通波门的清况下约为200毫秒。
所以杂波功率z2可以表示成两个独立随机变量的乘积:z2=XY
其中,X代表斑点分量,符合瑞利分布;Y代表调制部分,符合x2分布。
产生K分布杂波的过程如图2.8所示,随机序列是独立的、不相关的高斯分布随机向量。整个随机序列经过处理后,前θ个随机变量产生Y,剩余的两个随机变量生成X,这样K分布随机序列{zi}的PDF由X和Y乘积的平方根构成。
图2.8相关K分布序列产生方框图
Sij、Pij的关系为:

(2-21)
式(2-21)中,2F1(.)为高斯超几何分布函数,A=г(v+3/2)г(3/2)/г(v+l)
综上所述,产生相关K分布的具体步骤为:
(l)根据具体模拟目的的需要,适当选择△f,对于给定的功率谱密度函数S(f)进行采样得到序列{Sn’},其中n=1,2,…N。
(2)对于已得到的序列{Sn’},进行IFFT变换,获得所求的随机序列的自相关函数序列{Sn},其中n=1,2,…N。
(3)查Sij~rij曲线,求得{rij},其中n=1,2,…N。
(4)对序列{rij}进行FFT变换,得到随机序列X及Y的功率谱密度序列{uij}其中n=1,2,…N。
(5)产生相关高斯分布的随机序列{uij},其中i=1,2,…θ+2;n=1,2,…N。如果要求产生的K分布随机序列是时域的,那么,这里还要将产生的相关高斯分布的随机序列经过IFFT变换,变换到时城中,然后继续下面的运算。
(6)进行如图2.8所示的步骤,得到相关K分布随机序列

上面分析介绍了相关对数—正态分布、相关韦布尔分布和相关K分布杂波的计算机模拟方法,重点介绍了K分布相关杂波的模拟方法,因为随着雷达技术的进步和精度的提高,相关K分布模型被认为是描述地面和海洋等的杂波分布的最佳模型。
3 雷达系统杂波信号的仿真
在第二章我们对杂波的建模和仿真算法作了详细研究。完整的杂波仿真应该从实际条件出发,根据具体的雷达参数和环境参数,确定一个较为合理的杂波分布模型和功率谱模型,采用适当的适当的随机数产生方法来实现已知模型的杂波数据仿真。
在仿真中,杂波模块取用瑞利分布高斯谱杂波块,其它模块直接从工具箱里面调用。
3.1雷达系统的一般工作模型
我们知道,雷达发射信号和通讯机发射信号不同,通讯机的全部信号都在发射信号里,而雷达发射信号则毫无信息,它只是信号的运载工具,发射信号碰到目标后被返回为回波信号,回波信号还包括噪声和杂波。回波信号经过相干解调和抽样量化后返回目标信号。一般雷达系统的工作框如图3.1所示:
图3.1一般雷达系统的工作框图
在雷达系统中,我们用的发送信号为一个高频正弦波。对于目标回波,实际上它就是发送信号的一个时延,其大小为雷达发射波从信源到目标物所花的时间的两倍。系统噪声的加入由于外界环境的复杂性,我们假设回波传输是在一个理想的环境下进行的,即只存在高斯白噪声(Gaussian)和瑞利衰落信道下的噪声(Rayleigh Noise)。
3.2雷达系统中杂波信号的仿真
在仿真前,根据第二章的仿真方法,用M文件S函数编写十二种杂波模块,M文件代码见附录,图3.2为十二种杂波模块。

图3.2十二种杂波模块
把雷达系统做成Simulink下的仿真文件可以得到图3.3的仿真图形:

图3.3在Simulink中雷达系统仿真模型
①相参脉冲信号:
相参脉冲串信号可以写成以下形式:
s(t) = u(t) sinw0t (3-1)
u(t)为距形脉冲波,在这里设置T=1e-4,sinw0t为正弦波,设置w0= 1e52pi,图3.4是用Simulink建立的相参脉冲发生器框图,图3.5是相参脉冲波形图。

图3.4用Simulink建立的相参脉冲发生器框图

图3.5 发送端相参脉冲波形图
②回波信号:
在这里,假设delay为0.002ms,信号传送回来后幅度衰落为0.5,其回波波形如图3.6示:

图3.6无干扰噪声条件下回波信号波形图
③高斯白噪声信号:
在这里我们假设sigma=0.1,则波形如下图3.7示(sample time=1e-5):

图3.7 加性高斯白噪声信号
④杂波信号:
信号在自由空间里面传输,故我们还要加上杂波信号到系统中,假设加入的是瑞利分布高斯谱杂波,sigmac=0.1,波形如图图3.8示(sample time=1e-5)

图3.8瑞利噪声信号
⑤接收端的混频信号:
接收端混频信号由发送回波信号,高斯白噪声信号,和杂波信号组成。他们算术叠加就得到了接收端的混频信号。如图3.9所示。

图3.9 接收端的混频信号
⑥同步检测以后得到的信号
在雷达系统中其接收端采用相干解调来接收有用信号,故其波形如下图3.10所示:

图3.10 接收端相干解调后的信号
抽样判决后得到的信号波形和输入脉冲信号得到的波形如下图3.11所示

图3.11 抽样判决后的信号和输入脉冲信号
3.3雷达系统中其它杂波信号的仿真
在雷达杂波库建模与仿真时,可以产生常用的三种谱分布、四种幅度分布的交叉组合,共十二种参数任意的相关杂波。三种功率谱模型为:高斯谱、柯西谱、全极谱,四种幅度分布模型为:瑞利分布、对数正态分布、韦布尔分布、K分布。在上面仿真过程中,我们用的是瑞利分布高斯谱杂波,采用第二章所描述的模拟方法,我们可以生成其它十一种杂波模块,然后再放入雷达系统中进行仿真。在这里我们不详细进行仿真。
4 雷达系统性能分析
4.1瑞利杂波条件下雷达系统的性能分析
进行雷达系统性能分析时,在Simulink仿真框图的发射端加一个抽样量化模块和一个To Workspace模块,To Workspace模块变量名叫send,在接收端添加一个To Workspace模块,To Workspace模块变量名叫receive,把杂波模块的标准差改为变量b0。Simulink框图如下图4.1。

图4.1 在Simulink下雷达系统性能分析框图
然后建立一个M文件,改变变量b0的值,计算系统的漏检测概率。M文件代码见附录。写仿真时间设置为1s,在MATLAB窗口里运行M文件,得到一个随着变量b0改变而改变的漏检测概率曲线图,如图4.2。

图4.2雷达系统漏检测概率曲线图
由图可以看出,当瑞利杂波的标准差在0-0.85之间时,系统的漏检测概率基本为0,当标准差到了1之后,系统漏检测概率开始上升,而且上升的幅度比较大,当标准差到2时,系统漏检测概率已经到了0.2以上。由此可知,为了保持雷达系统的性能,瑞利杂波的标准差最好是在在0-1之间。
4.2 十二种不同杂波条件下雷达系统的性能比较
当改变雷达系统里面的杂波模块时,系统的性能同时也发生变化。在这里,我们把十二种杂波模块进行仿真并对比系统的漏检测概率曲线,如下图4.3,4.4,4.5。

图4.3 四种Gaussian杂波的漏检测概率曲线图

图4.4 四种Cauchy杂波的漏检测概率曲线图

图4.5 四种AllPole杂波的漏检测概率曲线图
由图4.3,4.4,4.5可知,当杂波的标准差比较小时,其杂波对雷达系统的影响不大,当标准差大于0.2时,系统性能明显发生了变化,漏检测概率曲线都随着杂波的标准差变大而变大,其中Rayleigh杂波的漏检测概率曲线变化比其它三种幅度分布杂波的变化小。所以,在Rayleigh杂波环境下雷达系统的性能较好。
5 结束语
本文主要研究雷达系统中的杂波信号的建模与仿真,在论文的开始部分介绍了十二种杂波模型的数学描述和仿真步骤,并成功的用MATLAB中的Simulink模块对其进行了仿真。
通过这些天的努力我学到了很多东西,能更好的综合运用在以前学习中学到的知识和自己通过相关方面的书的学习到的东西来进行简单语音信号的分析处理,进一步提高了自学能力与综合运用能力,也发现以前学的知识还是有不少漏洞的,弥补了自己的很多不足。
在此次仿真设计中碰到了许多问题,也学习到了许多知识。以后还需要有下面的工作:
(1)进一步了解雷达系统中杂波信号的相关知识。
(2)加强对MATLAB仿真工具的学习,使仿真更实际。
(3)进一步完善程序的设计,了解程序设计的技巧。
(4)以后要继续增强系统的理论知识,拓展知识面。
参考文献
[1]黄培康,许小剑.雷达目标特性[M].北京:电子工业出版社.2005
[2]李颖,朱伯立,张威.Simulink动态系统建模与仿真基础[M].西安:西安电子科技大学出版社.2004
[3]贾秋玲,袁冬莉,栾云凤.基于MATLAB 7.X/Simulink/Stateflow系统仿真、分析及设计[M].西安:西北工业大学出版社.2006
[4]左群声,徐国良等.雷达系统导论[M]. 北京:电子工业出版社.2006
[5]苏晓生.掌握MATLAB6.0及其工程应用[M].北京:科学出版社.2002
[6]张光义等. 空间探测相控阵雷达[M].北京:科学出版社.2001.
[7]弋稳.雷达接收机技术[M].北京:电子工业出版社.2005.4.
[8]何友等.雷达自动检测与恒虚警处理[M].北京:清华大学出版社.2 003
[9]花汉兵.雷达杂波模型的建立与仿真[J].计算机仿真,2007,24(10):92-94
[10]陈琳,等.雷达杂波基带调制数据的数学产生方法[J].雷达与对抗,2004, (1):43—46.
[11]Fred E.Nathanson.Radar design principles[J].SciTech,1999 , Vol.35 (No. 3)
[12]Xu X,Huang P K.A New RCS Statistical Model of Radar Targets[J].IEEE Trans.on Aweospace and Electronic Systems,1997, 33(2):698-709.
[13]J.B.Billingsley.Low-angle radar land clutter[M].William Andrew Publishing,2002
附录
附录A(sfun_RayleighGaussian.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=exp(-(400xl/(2pi)).2/(4*sigmac2));
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlDerivatives(t,x,u)
sys = [];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=w1*(sigmac^2);
sys=sqrt(2*w2^2);
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1;
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];
附录B(sfun_RayleighCauchy.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,fc)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^2);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=w1*(sigmac^2);
sys=sqrt(2*w2^2);
附录C(sfun_RayleighAllPole.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,fc,n)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^n);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=w1*(sigmac^2);
sys=sqrt(2*w2^2);
附录D(sfun_LogNormalGaussian.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,uc)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs0=exp(-(400xl/(2pi)).2/(4*sigmac2));
hrs=log(1+hrs0*(exp(sigmac2)-1))/sigmac2;
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac,uc);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac,uc)
w1 = filter(H,1,randn(1,1));
sys=exp(sigmac*w1+log(uc));
附录E(sfun_LogNormalCauchy.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,uc,fc)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs0=1./(1+((400xl./(2pi))./fc).^2);
hrs=log(1+hrs0*(exp(sigmac2)-1))/sigmac2;
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac,uc);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac,uc)
w1 = filter(H,1,randn(1,1));
sys=exp(sigmac*w1+log(uc));
附录F(sfun_LogNORMALAllPole.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,uc,fc,n)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs0=1./(1+((400xl./(2pi))./fc).^n);
hrs=log(1+hrs0*(exp(sigmac2)-1))/sigmac2;
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac,uc);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac,uc)
w1 = filter(H,1,randn(1,1));
sys=exp(sigmac*w1+log(uc));
附录G(sfun_WeibullGaussian.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,p,q)
sigmac=sqrt((q^p)/2);
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=exp(-(400xl/(2pi)).2/(4*sigmac2));
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,p,q);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,p,q)
w1 = filter(H,1,randn(1,1));
w2=w1sqrt(q^p/2);
sys=(2w22)(1/p);
附录H(sfun_WeibullCauchy.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,p,q,fc)
sigmac=sqrt((q^p)/2);
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^2);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,p,q);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,p,q)
w1 = filter(H,1,randn(1,1));
w2=w1sqrt((q^p)/2);
sys=(2w22)(1/p);
附录I(sfun_WeibullAllPole.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,p,q,fc,n)
sigmac=sqrt((q^p)/2);
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^n);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,p,q);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,p,q)
w1 = filter(H,1,randn(1,1));
w2=w1sqrt((q^p)/2);
sys=(2w22)(1/p);
附录J(sfun_KGaussian.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=exp(-(400xl/(2pi)).2/(4*sigmac2));
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=(2*(w1*sigmac)2)*(2*w12);
sys=sqrt(w2);
附录K(sfun_KCauchy.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,fc)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^2);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=(2*(w1*sigmac)2)*(2*w12);
sys=sqrt(w2);
附录L(sfun_KAllPole.m函数程序)
function [sys,x0,str,ts] = sfuntmpl(t,x,u,flag,st,sigmac,fc,n)
m=50;alpha=(m-1)/2;dw=2pi/m;
l=0:m-1;xl=dwl;
k1=0:floor((m-1)/2);k2=floor((m-1)/2)+1:m-1;
hrs=1./(1+((400xl./(2pi))./fc).^n);
angh=[-alphadwk1,alphadw(m-k2)];
H=hrs.exp(jangh);
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes(st);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u,H,sigmac);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes(st)
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs =0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [st 0];
function sys=mdlOutputs(t,x,u,H,sigmac)
w1 = filter(H,1,randn(1,1));
w2=(2*(w1*sigmac)2)*(2*w12);
sys=sqrt(w2);
附录M(瑞利杂波下系统的漏检测概率计算程序)
namda=[0.05:0.05:2];
for i=1:length(namda)
b0=namda(i);
sim(‘cgh2.mdl’);
l=length(send);
err_num=sum(receive(3:l)~=send(1:l-2));
err_fei(i)=err_num/l;
end
semilogy (namda,err_fei)
附录N(十二种常用杂波下系统的漏检测概率计算程序)
cgh_3.m
namda=[0.05:0.05:2];
for i=1:length(namda)
b0=namda(i);
sim(‘cgh2.mdl’);
l=length(send);
err_num1=sum(receive(3:l)~=send(1:l-2));
err_fei1(i)=err_num1/l;
sim(‘cgh3.mdl’);
l=length(send);
err_num2=sum(receive(3:l)~=send(1:l-2));
err_fei2(i)=err_num2/l;
sim(‘cgh4.mdl’);
l=length(send);
err_num3=sum(receive(3:l)~=send(1:l-2));
err_fei3(i)=err_num3/l;
sim(‘cgh5.mdl’);
l=length(send);
err_num4=sum(receive(3:l)~=send(1:l-2));
err_fei4(i)=err_num4/l;
end
semilogy(namda,err_fei1,‘b-*’,namda,err_fei2,‘g-o’,namda,err_fei3,‘r-x’,namda,err_fei4,‘y-p’);
legend(‘RayleighGaussian下漏检测概率曲线’,‘LogNormalGaussian下漏检测概率曲线’,‘WeibullGaussian下漏检测概率曲线’,‘KGaussian下漏检测概率曲线’);
cgh_4.m
namda=[0.05:0.05:2];
for i=1:length(namda)
b0=namda(i);
sim(‘cgh6.mdl’);
l=length(send);
err_num1=sum(receive(3:l)~=send(1:l-2));
err_fei1(i)=err_num1/l;
sim(‘cgh7.mdl’);
l=length(send);
err_num2=sum(receive(3:l)~=send(1:l-2));
err_fei2(i)=err_num2/l;
sim(‘cgh8.mdl’);
l=length(send);
err_num3=sum(receive(3:l)~=send(1:l-2));
err_fei3(i)=err_num3/l;
sim(‘cgh9.mdl’);
l=length(send);
err_num4=sum(receive(3:l)~=send(1:l-2));
err_fei4(i)=err_num4/l;
end
semilogy(namda,err_fei1,‘b-*’,namda,err_fei2,‘g-o’,namda,err_fei3,‘r-x’,namda,err_fei4,‘y-p’);
legend(‘RayleighCauchy下漏检测概率曲线’,‘LogNormalCauchy下漏检测概率曲线’,‘WeibullCauchy下漏检测概率曲线’,‘KCauchy下漏检测概率曲线’);
cgh_5.m
namda=[0.05:0.05:2];
for i=1:length(namda)
b0=namda(i);
sim(‘cgh10.mdl’);
l=length(send);
err_num1=sum(receive(3:l)~=send(1:l-2));
err_fei1(i)=err_num1/l;
sim(‘cgh11.mdl’);
l=length(send);
err_num2=sum(receive(3:l)~=send(1:l-2));
err_fei2(i)=err_num2/l;
sim(‘cgh12.mdl’);
l=length(send);
err_num3=sum(receive(3:l)~=send(1:l-2));
err_fei3(i)=err_num3/l;
sim(‘cgh13.mdl’);
l=length(send);
err_num4=sum(receive(3:l)~=send(1:l-2));
err_fei4(i)=err_num4/l;
end
semilogy(namda,err_fei1,‘b-*’,namda,err_fei2,‘g-o’,namda,err_fei3,‘r-x’,namda,err_fei4,‘y-p’);
legend(‘RayleighAllPole下漏检测概率曲线’,‘LogNormalLAllPole下漏检测概率曲线’,‘WeibullAllPole下漏检测概率曲线’,‘KAllPole下漏检测概率曲线’);
======================================================================
⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
完整文档下载地址链接
⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
=======================================================================