算法工程师重生之第十六天（二叉搜索树的最小绝对差 二叉搜索树中的众数 二叉树的最近公共祖先 ）

news2024/9/27 9:34:54

参考文献 代码随想录

一、二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

输入：root = [4,2,6,1,3]
输出：1

示例 2：

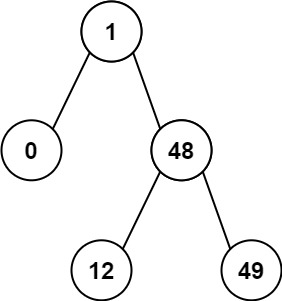
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

  • 树中节点的数目范围是 [2, 104]
  • 0 <= Node.val <= 105

暴力 

        利用中序遍历，然后取最小值，中序是升序的，所以它会让2个数相差 较小的在一起。

递归

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.resul = []

    def getMinimumDifference(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return
        self.getMinimumDifference(root.left)

        self.resul.append(root.val)
        self.getMinimumDifference(root.right)
        r = float("inf")
        for i in range(1, len(self.resul)):
            r = min(r, abs(self.resul[i] - self.resul[i - 1]))
        return r

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.resul = []

    def getMinimumDifference(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        from collections import deque
        stack = deque()
        stack.append(root)  # 左中右——>右中左
        while stack:
            cur = stack.pop()
            if cur:
                if cur.right: #  右
                    stack.append(cur.right)

                stack.append(cur) # 中
                stack.append(None)  # 标记 

                if cur.left: # 左
                    stack.append(cur.left)
            else:
                cur = stack.pop()
                self.resul.append(cur.val)


        r = float("inf")
        for i in range(1, len(self.resul)):
            r = min(r, abs(self.resul[i] - self.resul[i - 1]))
        return r

双指针的递归 

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.resul = float("inf")
        self.prev = None

    def getMinimumDifference(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return self.resul
        self.getMinimumDifference(root.left)

        if self.prev is not None:  # 为什么self.prev过不了
            self.resul = min(root.val - self.prev, self.resul)
        self.prev = root.val

        self.getMinimumDifference(root.right)
   
        return self.resul

1. self.prev is not None

  • 用途：这个表达式检查 self.prev 是否为 None。如果 self.prev 不等于 None，返回 True；否则返回 False。
  • 语义清晰：这种写法明确表示你在检查一个变量是否已被初始化或赋值。

2. self.prev

  • 用途：直接使用 self.prev 来判断其真值（truthiness）。如果 self.prev 为任何非零、非空的值（包括整数、字符串、列表等），则返回 True；如果是 None、0、''（空字符串）、[]（空列表）等，则返回 False。
  • 简洁性：这种写法更简洁，但不够明确，因为它不只检查 None，还会对其他“假”值进行评估。

总结

  • 使用 is not None 更加明确：在判断一个变量是否被赋值时，使用 self.prev is not None 更加清晰，能准确表达你的意图。
  • 使用 self.prev 则是更通用的检查：直接使用 self.prev 可以用于快速判断，而不仅限于检查是否为 None。

使用 self.prev is not None 是推荐做法，因为它确保了仅在 self.prev 被有效赋值后才执行相关逻辑，避免了潜在错误。

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.resul = float("inf")
        self.prev = None

    def getMinimumDifference(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        from collections import deque
        stack = deque()
        stack.append(root)  # 左中右——>右中左
        while stack:
            cur = stack.pop()
            if cur:
                if cur.right: #  右
                    stack.append(cur.right)

                stack.append(cur) # 中
                stack.append(None)  # 标记 

                if cur.left: # 左
                    stack.append(cur.left)
            else:
                cur = stack.pop()
                if self.prev is not  None:
                    self.resul = min(abs(self.prev - cur.val), self.resul)
                self.prev = cur.val

        return self.resul

二、二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

  • 结点左子树中所含节点的值 小于等于 当前节点的值
  • 结点右子树中所含节点的值 大于等于 当前节点的值
  • 左子树和右子树都是二叉搜索树

示例 1：

输入：root = [1,null,2,2]
输出：[2]

示例 2：

输入：root = [0]
输出：[0]

提示：

  • 树中节点的数目在范围 [1, 104] 内
  • -105 <= Node.val <= 105

暴力

        遍历加统计然后排序

递归 

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.r = 0
        self.dict = {}

    def findMode(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        li = []
        self.dfs(root)
        self.r =  sorted(self.dict.items(), key = lambda x:x[1], reverse = True)
        k, v = self.r[0]
        li.append(k)
        for i in range(1, len(self.r)):
            if self.r[i][1] == v:
                li.append(self.r[i][0])
            else:
                break
        return li
    def dfs(self, cur):
        if not cur: # 如果当前为空
            return
        self.dfs(cur.left)
        if  cur.val in self.dict:
            self.dict[cur.val] += 1
        else:
            self.dict[cur.val]  = 1
        self.dfs(cur.right)

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.r = 0
        self.dict = {}

    def findMode(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        from collections import deque
        stack = deque()
        stack.append(root)
        while stack:
            cur = stack.pop()
            if cur:
                if cur.right:
                    stack.append(cur.right)
                stack.append(cur)
                stack.append(None)
                if cur.left:
                    stack.append(cur.left)
            else:
                cur = stack.pop()
                if cur.val not in self.dict:
                    self.dict[cur.val] = 1
                else:
                    self.dict[cur.val] += 1
        li = []
        self.r =  sorted(self.dict.items(), key = lambda x:x[1], reverse = True)
        k, v = self.r[0]
        li.append(k)
        for i in range(1, len(self.r)):
            if self.r[i][1] == v:
                li.append(self.r[i][0])
            else:
                break
        return li

双指针递归：这是利用一个count变量统计每天出现的 次数 ，初始化为1，因为最少出现 一次，还有一个数组存放的是最后的结果集 ，还需要一个变量来存放最高次出现的次数，利用的是中序遍历，为什么？因为它的性质，得到的 结果是升序的，这样就可以让相同的数挨到一起，以便统计出现 的次数，如果前一个节点不为空，如果前一个节点的值等于当前 节点的值，那么对应的次数 加一 ，否则初始为1，然后如果当前元素对应的次数 等于最高次的，那么就要 添加（最高次一定是最高次吗？）别急 ，后面判断，如果当前 的次数大于最高次 ，那么就要初始化结果数组 ，并添加。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.prev = None
        self.result = []  # 存放的是结果
        self.count = 1   # 对应的次数
        self.maxCount = float("-inf")
    def findMode(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not  root:
            return
        self.findMode(root.left)

        if self.prev is not None:   # 这里统计每个元素出现的次数
            if  self.prev == root.val:
                self.count += 1
            else:
                self.count =1
        self.prev = root.val

        if self.count == self.maxCount:    # 如果 当前元素出现的次数等于最大高次的 次数，就要条件 （这里的最高次不一定为最高 ）
            self.result.append(root.val)

        if self.count > self.maxCount:   # 如果当前的次数大于最大的次数，那么就要清空，然后在添加  
            self.maxCount = self.count
            self.result = []
            self.result.append(root.val)

        self.findMode(root.right)
        return self.result

迭代

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.prev = None    # 记录前一个节点
        self.result = []  # 存放的是结果
        self.count = 1   # 对应的次数
        self.maxCount = float("-inf")   # 存放的是二叉树中出现最高次的次数 
    def findMode(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        from collections import deque
        stack = deque()
        stack.append(root)
        while stack:
            cur = stack.pop()
            if cur:
                if cur.right:
                    stack.append(cur.right)
                stack.append(cur)
                stack.append(None)
                if cur.left:
                    stack.append(cur.left)
            else:
                cur = stack.pop()

                if self.prev is not None:
                    if self.prev == cur.val:  # 当前值  等于 前一个的值，那么就要加1，否者为1
                        self.count += 1
                    else:
                        self.count = 1

                self.prev = cur.val

                if self.count == self.maxCount:   # 等于就要收集结果 
                    self.result.append(cur.val)

                if self.count > self.maxCount: # 如果对应的节点 出现 的次数 大于  最大的 ，那么就要更改
                    self.maxCount = self.count
                    self.result = [cur.val]   #  并添加 
        return self.result

三、二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

  • 树中节点数目在范围 [2, 105] 内。
  • -109 <= Node.val <= 109
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。

问题分析 

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？

回溯啊，二叉树回溯的过程就是从低到上。

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。

接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。 即情况一：

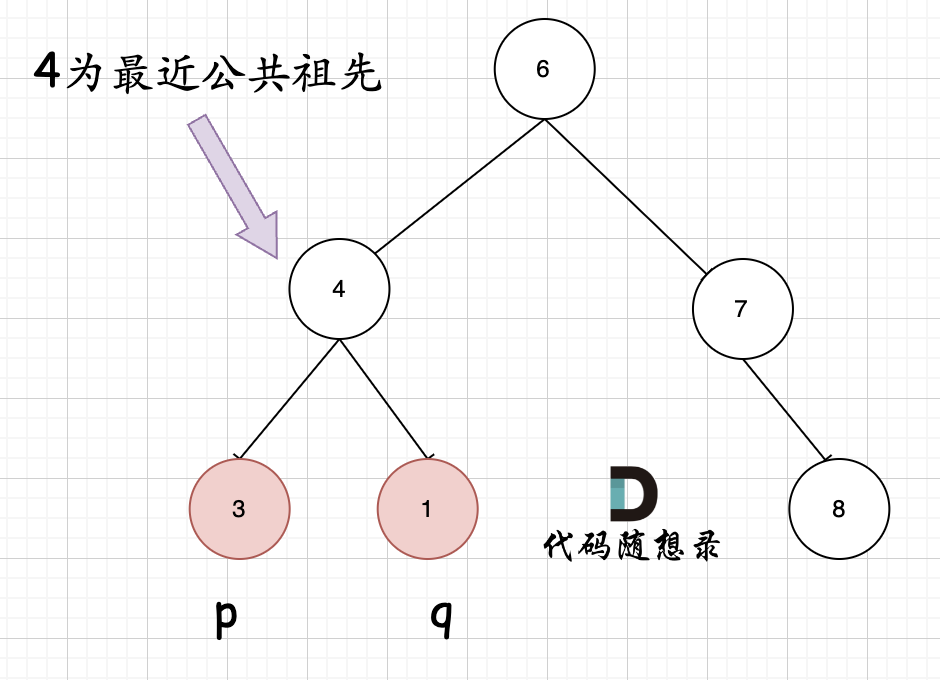
判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。

那么有录友可能疑惑，会不会左子树 遇到q 返回，右子树也遇到q返回，这样并没有找到 q 和p的最近祖先。

这么想的录友，要审题了，题目强调：二叉树节点数值是不重复的，而且一定存在 q 和 p。

但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。 情况二：

其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。

因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。

这一点是很多录友容易忽略的，在下面的代码讲解中，可以再去体会。

递归三部曲：

  • 确定递归函数返回值以及参数

需要递归函数返回值，来告诉我们是否找到节点q或者p，那么返回值为bool类型就可以了。

但我们还要返回最近公共节点，可以利用上题目中返回值是TreeNode * ，那么如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

代码如下：

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)

1

  • 确定终止条件

遇到空的话，因为树都是空了，所以返回空。

那么我们来说一说，如果 root == q，或者 root == p，说明找到 q p ，则将其返回，这个返回值，后面在中节点的处理过程中会用到，那么中节点的处理逻辑，下面讲解。

代码如下：

if (root == q || root == p || root == NULL) return root;
  • 确定单层递归逻辑

值得注意的是 本题函数有返回值，是因为回溯的过程需要递归函数的返回值做判断，但本题我们依然要遍历树的所有节点。

我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？ (opens new window)中说了 递归函数有返回值就是要遍历某一条边，但有返回值也要看如何处理返回值！

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中

看出区别了没？

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

那么为什么要遍历整棵树呢？直观上来看，找到最近公共祖先，直接一路返回就可以了。

如图：

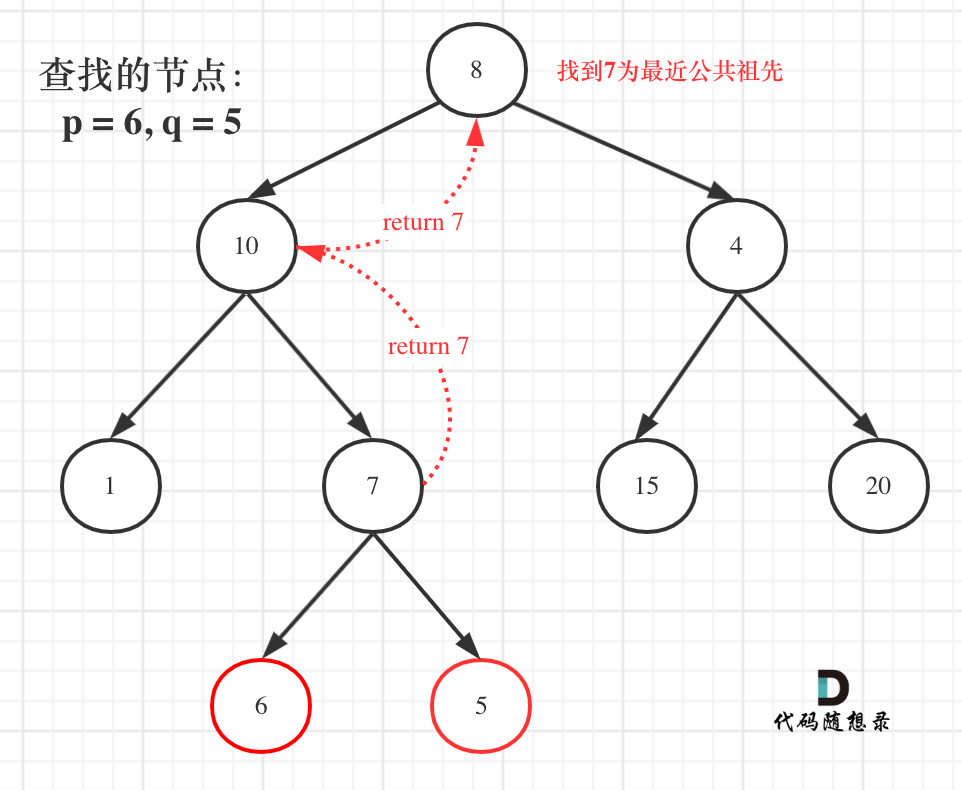
236.二叉树的最近公共祖先

就像图中一样直接返回7。

但事实上还要遍历根节点右子树（即使此时已经找到了目标节点了），也就是图中的节点4、15、20。

因为在如下代码的后序遍历中，如果想利用left和right做逻辑处理， 不能立刻返回，而是要等left与right逻辑处理完之后才能返回。

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中

所以此时大家要知道我们要遍历整棵树。知道这一点，对本题就有一定深度的理解了。

那么先用left和right接住左子树和右子树的返回值，代码如下：

TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);

如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

这里有的同学就理解不了了，为什么left为空，right不为空，目标节点通过right返回呢？

如图：

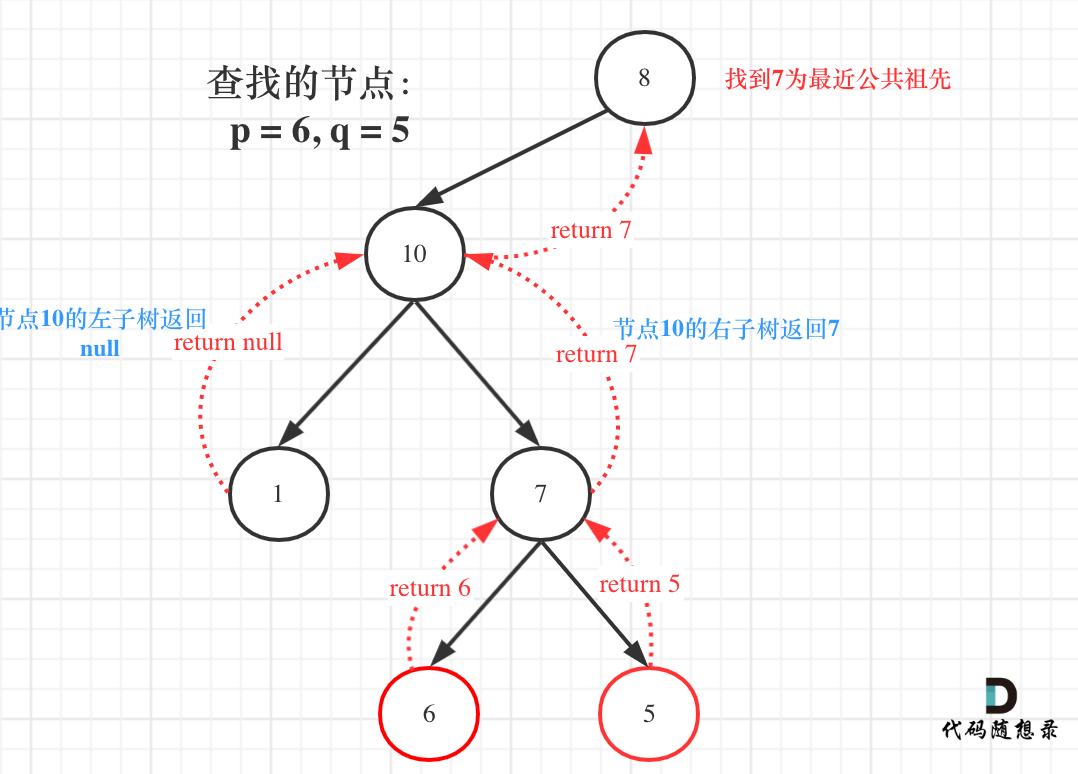
236.二叉树的最近公共祖先1

图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

代码如下：

if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else  { //  (left == NULL && right == NULL)
    return NULL;
}

那么寻找最小公共祖先，完整流程图如下：

236.二叉树的最近公共祖先2

从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！

  1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。

  2. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

  3. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

总的思路：通过后序遍历，来判断左右是否出现过p或者是q然后一直返回。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if not root:  #  如果为空那么就直接返回
            return

        if root.val == p.val or root.val == q.val: # 如果当前的节点等于q后者是p直接返回  ，返回值是是否是最近公共祖先
            return root

        left = self.lowestCommonAncestor(root.left, p, q)  # 返回左 
        right = self.lowestCommonAncestor(root.right, p, q)    # 返回有 右
         
        if left and right:  #如果左右都出现过，那么就直接返回 
            return root
        if left and not right:  # 如果左不为空，就直接返回左
            return left
        elif not left and right:# 如果右不为空，就直接返回有
            return right
        else:  # 2个都为空，直接返回空
            return
        return root

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2169585.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

语义元分割学习：一种用于少量样本无线图像分类的TinyML方案

语义元分割学习：一种用于少量样本无线图像分类的TinyML方案

论文标题&#xff1a;Semantic Meta-Split Learning: A TinyML Scheme for Few-Shot Wireless Image Classification 中文标题&#xff1a;语义元分割学习&#xff1a;一种用于少量样本无线图像分类的TinyML方案 作者信息&#xff1a; Eslam Eldeeb, Mohammad Shehab, Hirley…
阅读更多...
nvm，一款nodejs版本管理工具

nvm，一款nodejs版本管理工具

背景 在工作中&#xff0c;我们可能同时在进行2个或者多个不同的项目开发&#xff0c;每个项目的需求不同&#xff0c;进而不同项目必须依赖不同版本的NodeJS运行环境&#xff0c;这种情况下&#xff0c;对于维护多个版本的node将会是一件非常麻烦的事情&#xff0c;nvm就是为…
阅读更多...
Dapper 如何确保数据的安全性和防止 SQL 注入攻击？

Dapper 如何确保数据的安全性和防止 SQL 注入攻击？

一、什么是SQL注入攻击 SQL注入攻击是一种常见的网络攻击手段&#xff0c;它利用了应用程序中安全措施不足的问题&#xff0c;允许攻击者插入或“注入”一个或多个SQL语句到原本的查询中。这种攻击可以用于获取、篡改或删除数据库中的数据&#xff0c;甚至可以执行一些数据库管…
阅读更多...
java：brew安装rabbitmq以及简单示例

java：brew安装rabbitmq以及简单示例

什么是消息队列mq 可以看我之前写的这篇 消息队列MQ rabbitmq简介 RabbitMQ是由erlang语言开发&#xff0c;基于AMQP&#xff08;Advanced Message Queue 高级消息队列协议&#xff09;协议实现的消息队列&#xff0c;它是一种应用程序之间的通信方法&#xff0c;消息队列在…
阅读更多...
200smart数据日志的功能

200smart数据日志的功能

称重设备&#xff08;皮带秤&#xff09;读取到的数据值总是一直在跳变&#xff0c;无法正确识别称重传感器读取上来的值来判断产品的重量&#xff0c;虽然在程序中增加了取平均值功能&#xff08;模拟量输入按PLC扫描周期次数求平均值程序&#xff09;&#xff0c;但效果不理想…
阅读更多...
什么是聚集索引？

什么是聚集索引？

什么是聚集索引&#xff1f; 1、聚集索引的特点2、如何确定聚集索引3、性能优势 &#x1f496;The Begin&#x1f496;点点关注&#xff0c;收藏不迷路&#x1f496; 聚集索引是一种特殊的索引&#xff0c;它直接包含了表中的所有数据行。所以&#xff0c;通过聚集索引&#xf…
阅读更多...
代码随想录冲冲冲 Day56 图论Part8

代码随想录冲冲冲 Day56 图论Part8

117. 软件构建 这道题是使用拓扑排序的方法 看多个任务有优先级的情况下 怎么排序 对应到这道题就是文件排序 首先要记录每一个点的入度&#xff0c;当一个点的入度为0时&#xff0c;就说明这个点是顶点 然后记录每一个点向那些点相连 之后建立一个queue 寻找一个入度为0的…
阅读更多...
弹簧状态检测系统源码分享

弹簧状态检测系统源码分享

弹簧状态检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer Vis…
阅读更多...
Linux中安装ffmpeg

Linux中安装ffmpeg

Linux中安装ffmpeg 一、下载二、安装三、测试 一、下载 先到这里下载ffmpeg。 二、安装 先将上传到服务器的某一目录&#xff0c;我这里是&#xff1a; /usr/local/ffmpeg 然后解压&#xff0c;解压命令如下&#xff1a; tar -xvf “你的安装包名称”我的是&#xff1a; ta…
阅读更多...
流浪软件uniaccess agent 删除

流浪软件uniaccess agent 删除

cmd的C盘找不到就用git rm -rf 之后&#xff0c;只剩下 俩文件夹删不掉 然后360软件就看到了&#xff0c;可惜卸载失败 然后360文件就找到了&#xff0c;彻底删除 再回git 查看 方法 https://blog.51cto.com/u_16099347/11352333 https://blog.csdn.net/xioayu96/article/…
阅读更多...
Linux下线程间的通信

Linux下线程间的通信

为什么需要线程通信&#xff1f; 线程是操作系统调度的最小单元&#xff0c;拥有自己的栈空间。如果线程之间孤立运行&#xff0c;可能会导致资源浪费。线程需要协调工作以完成共同的任务&#xff0c;这就需要线程间相互通信 在 Linux 系统中&#xff0c;线程间通信&#xff…
阅读更多...
请问这张图是ai绘画吗？

请问这张图是ai绘画吗？

小白可做&#xff01;全自动AI影视解说一键成片剪辑工具https://docs.qq.com/doc/DYnl6d0FLdHp0V2ll 先来结论&#xff0c;找到用这图的某宝店老板了&#xff0c;老板说不是AI画的。 真相只有一个&#xff0c;有图有真相 再来化身柯南&#xff0c;看看寻找答案的过程 要判断这张…
阅读更多...
重考！CSP-J/S 2024第一轮认证泄题后续进展及疑问

重考！CSP-J/S 2024第一轮认证泄题后续进展及疑问

2024年9月26日晚间&#xff0c;NOI官网发布了”对部分被认证者进行CSP-J/S 2024第一轮重新认证的公告“&#xff0c;对少儿编程培训机构老师举报陕西鸿泉教育培训机构泄题一事进行了最新的回应。 对涉嫌参加该机构培训的学生的CSP-J/S 2024第一轮入门级、提高级认证成绩不予认可…
阅读更多...
＜＜编码＞＞ 第 21 章 总线连接(Get on the Bus) 示例电路

＜＜编码＞＞ 第 21 章 总线连接(Get on the Bus) 示例电路

比较器 info::操作说明 鼠标单击开关切换开合状态 鼠标单击逻辑输入切换 0|1 状态 若上方和左边的输入相同, 则输出高电平 primary::在线交互操作链接 https://cc.xiaogd.net/?startCircuitLinkhttps://book.xiaogd.net/code-hlchs-examples/assets/circuit/code-hlchs-ch21-0…
阅读更多...
力扣（LeetCode)每日一题 2207. 字符串中最多数目的子序列

力扣（LeetCode)每日一题 2207. 字符串中最多数目的子序列

题目链接https://leetcode.cn/problems/maximize-number-of-subsequences-in-a-string/description/?envTypedaily-question&envId2024-09-24 给你一个下标从 0 开始的字符串 text 和另一个下标从 0 开始且长度为 2 的字符串 pattern &#xff0c;两者都只包含小写英文字母…
阅读更多...
Vue中使用Hls.js进行视频直播的播放

Vue中使用Hls.js进行视频直播的播放

HLS.js使用文档 1、安装组件&#xff1a; npm install hls.js --save2、引入组件&#xff1a; import Hls from hls.js3、使用组件&#xff1a; // DOM&#xff1a; <video id"video" controls loop"false"></video> // DATA: let hls nul…
阅读更多...
[深度学习]卷积神经网络CNN

[深度学习]卷积神经网络CNN

1 图像基础知识 import numpy as np import matplotlib.pyplot as plt # 图像数据 #imgnp.zeros((200,200,3)) imgnp.full((200,200,3),255) # 可视化 plt.imshow(img) plt.show() # 图像读取 imgplt.imread(img.jpg) plt.imshow(img) plt.show() 2 CNN概述 卷积层convrelu池…
阅读更多...
实战OpenCV之色彩空间转换

实战OpenCV之色彩空间转换

基础入门 色彩空间是描述颜色的一种数学模型&#xff0c;它定义了颜色的三个或更多维度&#xff0c;比如&#xff1a;亮度、色相和饱和度等。最著名的色彩空间之一是RGB&#xff0c;它基于人眼对光的感知原理&#xff0c;通过红、绿、蓝三种基本颜色的不同强度组合来表示几乎所…
阅读更多...
【HarmonyOS】鸿蒙仿iOS线性渐变实现

【HarmonyOS】鸿蒙仿iOS线性渐变实现

【HarmonyOS】仿照IOS中可以通过输入start&#xff08;0&#xff0c;0&#xff09;&#xff0c;end&#xff08;1&#xff0c;1&#xff09;获取角度到.linearGradient&#xff0c;从而实现左上到右下渐变 class Point {x: number 0y: number 0 }Entry Component struct Page…
阅读更多...
开源链动 2+1 模式 S2B2C 商城小程序：激活 KOC，开启商业新征程

开源链动 2+1 模式 S2B2C 商城小程序：激活 KOC，开启商业新征程

摘要&#xff1a;本文深入探讨了 KOC 在立体连接中的重要性&#xff0c;以及如何通过开源链动 21 模式 S2B2C 商城小程序发现和找到更多的 KOC。强调了历史积累强关系和快速强化强关系的方法&#xff0c;并阐述了该商城小程序在推动商业发展中的关键作用。 一、引言 在当今竞争…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023