摘要：

1，约翰逊算法的介绍

2，约翰逊算法的实现步骤

3，约翰逊算法的准确性验证

4，约翰逊算法的代码实现

1，约翰逊算法的介绍

约翰逊算法(Johnson algorithm)是在稀疏图上求每对顶点之间最短路径的一种算法，该算法在 1977 年由 Donald B. Johnson 提出。

在前面我们讲过求任意两对顶点之间的最短路径可以使用《Floyd算法》，它可以解决有负权边的图，但不能有负权回路，它的时间复杂度是O(n^3)，非常高。

我们知道《迪杰斯特拉算法》是求单源点最短路径的，也就是计算从一个点到其它所有点的最短距离。

而堆优化的迪杰斯特拉算法时间复杂度是O((V+E)logV)，如果是稀疏图的话，边的数量 E 就会比较小，我们可以以每一个顶点为起始点跑一遍迪杰斯特拉算法即可求出任意两点之间的最短路径。

但迪杰斯特拉算法有个缺点就是不能有负权边，这个时候我们可能想到的是，给每一条边都加上一个值，让它们都变成正的就好了，但这样也是不行的，如下图所示：

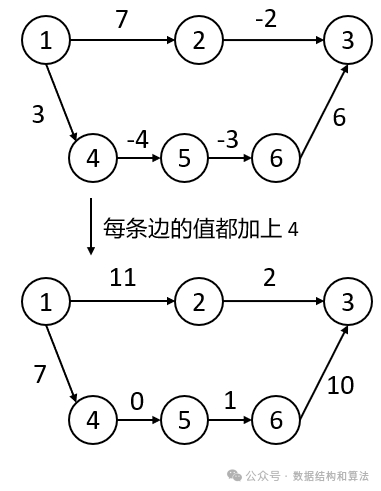
在上图中从顶点 1 到顶点 3 的最短路径本来是 1→4→5→6→3，长度为 2。如果我们把每条边都加上 4 ，这样边的权值虽然没有负数了，但从顶点 1 到顶点 3 的最短路径也改变了，变成了 1→2→3 ，长度为13，已经不是原来的最短路径了，原来的最短路径 1→4→5→6→3 长度变成了 18 。

这是因为原来的最短路径经过的边数比较多，如果每条边都加同一个值，原来的最短路径累加的值就越大，就可能导致最短路径发生改变。

这个时候我们可以考虑使用Johnson 算法，Johnson 算法就是通过另外一种方式来给每条边重新标注权值。

2，约翰逊算法的实现步骤

Johnson算法的精髓就是预处理，确保所有边的权值均非负。使用Johnson算法我们需要添加一个虚拟节点(这里我们假设它的编号为 0 )，这个虚拟节点指向其它所有的顶点，并且权值都为 0 ，如下图所示：

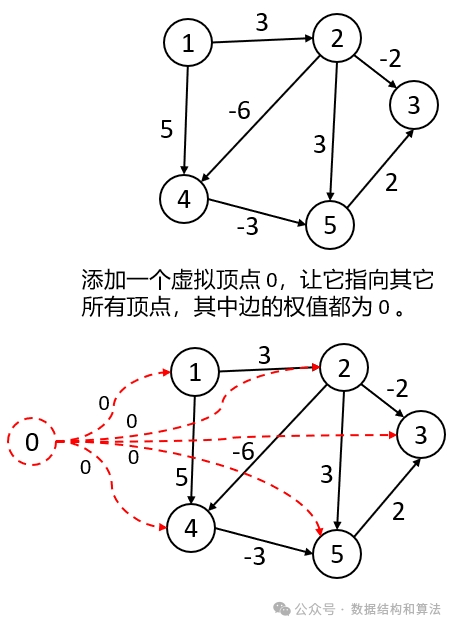
然后我们使用《贝尔曼-福特算法(Bellman-Ford)》或者《SPFA算法》来计算从顶点 0 到其它所有顶点的最短距离dis[n]。

接着再给所有的边重新赋值，将w(u,v)变成w(u,v)' = w(u,v) + dis(u) - dis(v)，w(u,v)是原来边<u,v>的权值，w(u,v)'重新赋值之后的权值。