数据结构入门学习(全是干货)——综合应用
习题选讲 - 排序与字符串匹配算法
习题选讲 - Insert or Merge
习题-IOM.1 插入排序的判断
题意理解
如何区分简单插入和非递归的归并排序
- 插入排序:前面有序,后面没有变化。
- 归并排序:分段有序。

捏软柿子算法
- 在插入和归并两种算法里,判断插入排序较容易。
判断是否为插入排序
- 从左向右扫描,直到发现顺序不对,跳出循环。
- 从跳出地点继续向右扫描,与原始序列比对,若发现不同,则判断为“非插入排序”。如果在对比过程中发现不同,跳出循环。
- 循环自然结束,则判断为“是”,返回跳出地点。
解析:可以返回一个布尔值,例如非为0、是为1,但如果返回“是”,插入排序需继续进行,从左向右扫描找到执行下一步的地点。因此返回“是”的同时返回跳出地点。
如果是插入排序,则从跳出地点开始进行一趟插入。
习题-IOM.2 归并段的判断
判断归并段的长度
错误的想法:
- 从头开始连续有序的子列长度?

- 所有连续有序子列的最短长度?

- 保险的判断方法:从原始序列出发,真正进行归并排序。每归并一趟就将归并的中间结果与当前序列做比对,什么时候每一个数都对上了就继续执行。
for (l=2;l<=N;l*=2)
//在保证了l是4的情况下,要检查看能不能是8,我们要重复前面的步骤看两段之间的衔接点是不是有序

- 红色位置没有序了时跳出循环,此时l为4,直接以4为归并段继续执行下一趟的归并。

其他数据测试
最小N(应该多大?)
边界测试是每道题的关键组成部分。
- N等于1时,序列仅一个数字,排序前后结果相同,因此解不唯一。要求区分两种算法的最小N为4:
- 插入排序第一步,无变化。
- 归并排序第一步,所有元素变了。
最大N
习题选讲 - Sort with Swap(0,*)
习题-SWS.1 环的分类
题意理解
- 给定N个数字的排列,如何仅利用与0交换达到排序目的?0扮演空位的角色。
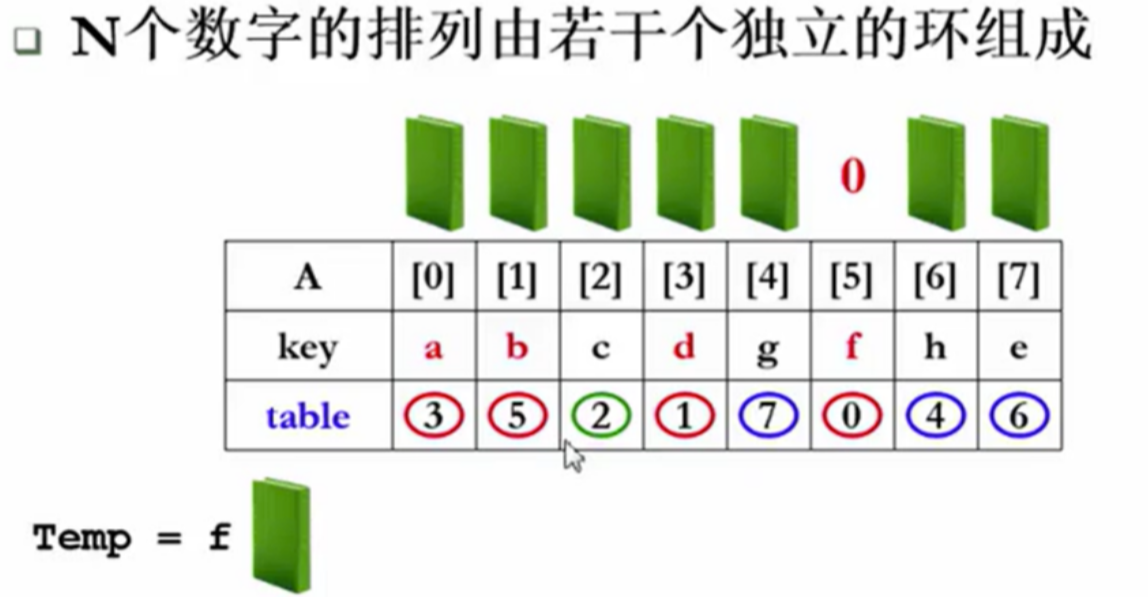
环的分类

习题-SWS.2 算法示例
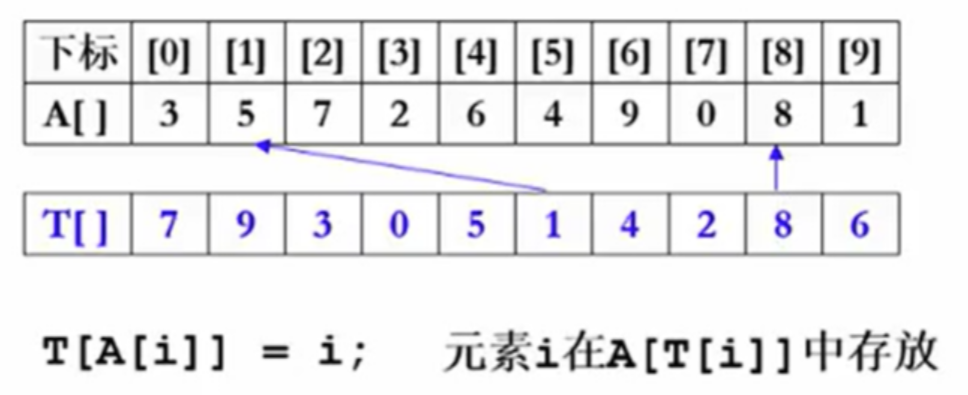
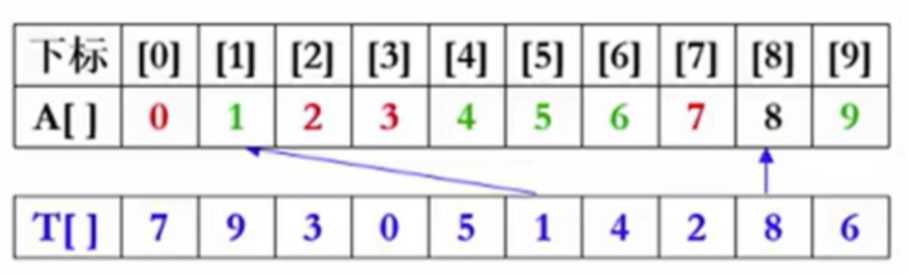
对于不包含0的交换操作次数为n+1,包含0则是n-1次。
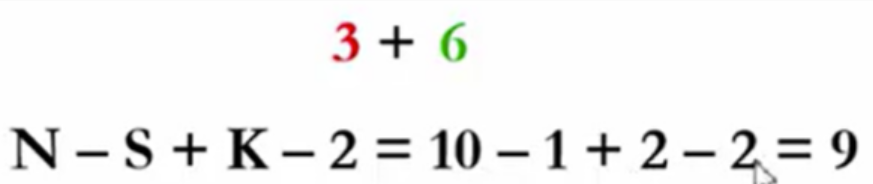
习题选讲 - Hashing - Hard Version
习题-HHV 算法思路概述
这是哈希问题的逆问题
题意理解
- 已知H(x) = x%N,利用线性探测解决冲突问题。
- 先给出散列映射的结果,反求输入顺序。
- 当元素x被映射到H(x)位置,发现该位置已被y占用,则y一定在x之前被输入。
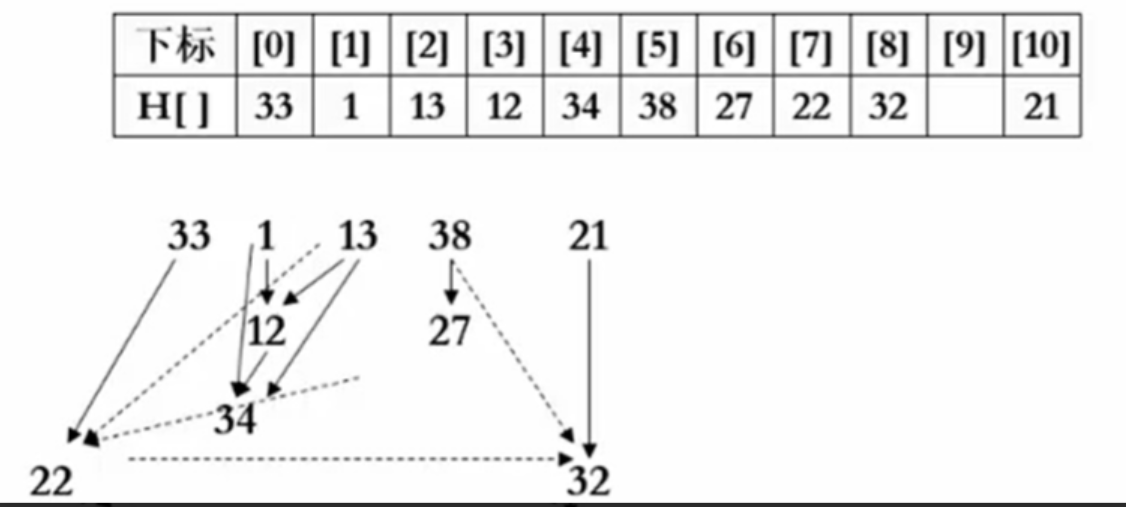
限制:为确保解唯一,若几个元素可能同时被插入,则按从小到大顺序插入。
因为12模11,余数为1,所以跟12冲突,放在12下面。后面都是类型的操作
依次输入顺序为
串的模式匹配(KMP算法)
KMP-1. 问题及简单解决方案
什么是串
-
线性存储的一组数据(默认是字符)。
-
特殊操作集。
1.求串的长度 2.比较两串是否相等 3.两串相接 4.求子串 5.插入子串 6.匹配子串(有难度) 7.删除子串
什么是串的模式匹配
目标:给定一段文本,从中找出某个指定的关键字
例如从一本Thomas Love Peacock写于十九世纪的小说《Headlong Hall》中找到那个最长的单词: osseocarnisanguineoviscericartilaginonervomedullary
或者从古希腊喜剧《Assemblywomen》中找到一道菜的名字: Lopadotemachoselachogaleokranioleipsanodrimhypotrimmatosilphioparaomelitokatakechymenokichlepikossyphophattoperisteralektryonoptekephalliokigklopeleiolagoiosiraiobaphetraganopterygon
模式匹配目标
- 给定文本,从中找出指定的关键字。

Position PatterMatch(char *string,char *pattern)//position指位置
//模式匹配就是给定一段文本(string),给定一个模式(*pattern),我们要通过PatterMatch函数来返回这个pattern里string第一次出现的位置
简单实现
方法1:C语言库函数strstr。
接口:char *strstr(char *string,char *pattern)
//返回的是char *这个类型的变量(指向某个字符的指针),变量里面存的是pattern这个字符串第一个字母在string出现的时候那个字母所在的位置
//一个小Demo
#include <stdio.h>
#include <string.h>//库要记得包含进来
typedef char* Position;//给char*重新起个名字,让不懂的人也可以知道返回的是一个位置
int main()
{
char string[] = "This is a simple example.";
char pattern[] = "simple";
Position p = strstr(string,pattern);
if( p == NotFound ) printf("Mot Found.\n");//能不能找到进行一个判断
else printf("%s\n",p);
return 0;
}
//输出:simple example.
//如果输入的找不到,就会输出一个空指针(#define NotFound NULL)

- strstr的最坏时间复杂度为O(nm),当模式较小时可用,但当两者都较大时需谨慎。
简单改进
方法2:从末尾开始比。

时间复杂度:T = O(n)//仅仅是根据上方的例子进行的改动,如果pattern = "aab"换成"baa"一样要芭比Q
所以这个改进是没啥作用的
KMP-2. KMP 算法思路
大师改进
方法3:KMP算法,时间复杂度为O(n+m)。
-
简单的往前错一位的比较是完全没有必要的没有意义的,如下图
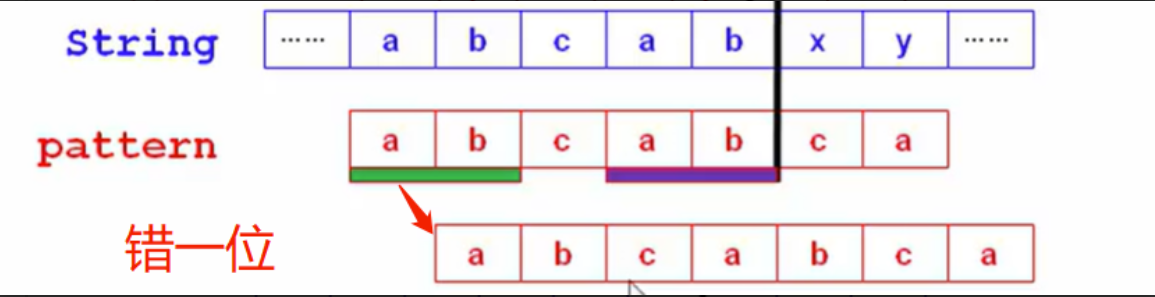
-
KMP算法的想法:

-
指针x不回退,继续从x开始比较。
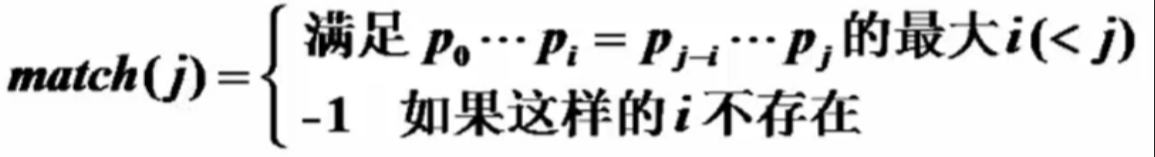
match的具体例子

下标从0到9
第0个字符对应的是一个长度为1的子串,所以他不可能产生匹配,match就永远是-1
从0到1:a跟b是配不上的,match也为-1
0-2:a和c配不上,ab和bc也配不上,所以match还是为-1
0-3:ab和ca是配不上的,abc跟bca也配不上,a对应的j为0,所以match也为0
//此时限制条件是最大i是小于j的,如果i=j的话那就相当于自己等于自己就没有意义了(p0...pj = p0...pj)
//所以我们考虑他的真子串
0-4:a跟b配不上,abc跟cab配不上,ab跟ab能配上,match值为1...
- 对于pattern = abcabcacab,最后3个字符的match值为-1, 0, 1。
对于 pattern = abcabcacab,最后 3 个字符的 match 值是多少?-1, 0, 1
在早期的教科书上被叫做failure(失败的意思)
match值的含义:
例子:从0到6的子串,首跟尾能配上的小串,从0开始他的尾部下标为3,abca跟abca能配上。这就是match的含义
此代码块内容来自百度百科:
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)
KMP算法是三位学者在 Brute-Force算法的基础上同时提出的模式匹配的改进算法。Brute- Force算法在模式串中有多个字符和主串中的若干个连续字符比较都相等,但最后一个字符比较不相等时,主串的比较位置需要回退。KMP算法在上述情况下,主串位置不需要回退,从而可以大大提高效率
模式匹配类型
(1)精确匹配
如果在目标T中至少一处存在模式P,则称匹配成功,否则即使目标与模式只有一个字符不同也不能称为匹配成功,即匹配失败。给定一个字符或符号组成的字符串目标对象T和一个字符串模式P,模式匹配的目的是在目标T中搜索与模式P完全相同的子串,返回T和P匹配的第一个字符串的首字母位置 。
(2)近似匹配
如果模式P与目标T(或其子串)存在某种程度的相似,则认为匹配成功。常用的衡量字符串相似度的方法是根据一个串转换成另一个串所需的基本操作数目来确定。基本操作由字符串的插入、删除和替换来组成
KMP-3. KMP 算法实现
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)
KMP算法是三位学者在 Brute-Force算法的基础上同时提出的模式匹配的改进算法。Brute- Force算法在模式串中有多个字符和主串中的若干个连续字符比较都相等,但最后一个字符比较不相等时,主串的比较位置需要回退。KMP算法在上述情况下,主串位置不需要回退,从而可以大大提高效率
- KMP算法实现示意。

一直走到指针不匹配

Position KMP(char *string,char *pattern )
{
int n = strlen(string);//strlen得到string的长度,下方也是一样 复杂度:O(n)
int m = strlen(pattern);//复杂度:O(m)
int s,p,*match;//声明两个指针
if(n < m) return NotFound;//找的n不可能比m短
match = (int *)malloc(sizeof(int) *m);
BuildMatch(pattern,match);//Tm = O(?)
s = p =0;
while( s<n &&p<m){ //当这两个指针一起往前飞,任何一个指针先指到自己指的串的末尾的时候结束,复杂度O(n)
if(string[s] == pattern[p]){ s++;p++; }//p有时候加加有时候回退,但s永远加加
else if (p>0) p = match[p-1]+1;//为了防止得到段错误,这里加上条件p>0
//如果p = 0的话,意味着pattern从第一个字符就不匹配,这个时候p不动,s向前走一格
else s++;//当string[s] == pattern[p]不匹配,我们s++,继续下一轮匹配
}
//在我们跳出while循环的时候,p指针已经碰到pattern的末尾(p==m),那就是完全的匹配上了
//反之p还没有到结尾,而string已经到p的结尾了,就意味着我们找不到这个模式
return (p == m) ? (s-m) : NotFound;
}


KMP的整体时间复杂度
- T = O(n+m+Tm)。
KMP-4. BuildMatch 的实现原理

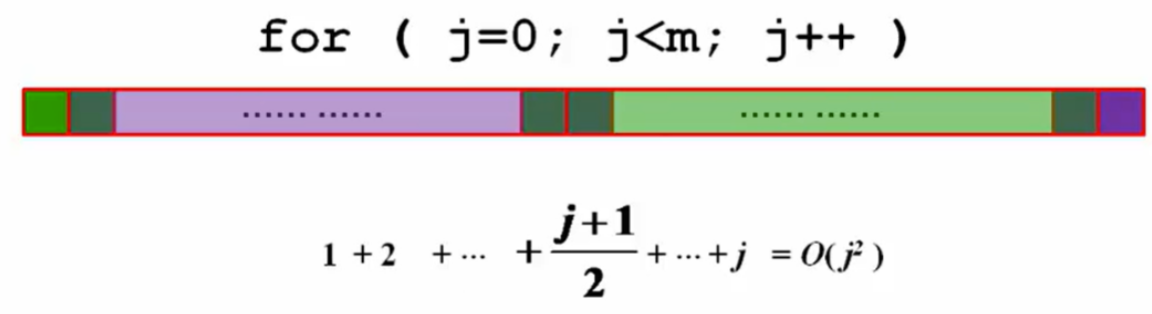
- 如果采用这种方法,时间复杂度将达到Tm = O(m³)。
新想法:计算j的match值与j-1的match值的关系。
假如我们这是从0到j-1的字段

- match[j] = match[j-1] + 1(最多持平)。
如果 match[j-1]+1 这个位置上的字符与 j 位置上的字符相等,match[j] 会有可能比 match[j-1]+1 更大吗?没可能
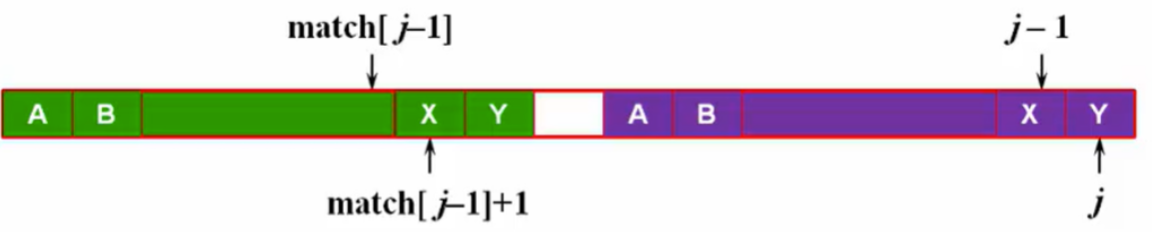
match[j] = match[j-1] + 1 (最多持平啦,利用反证法证明)
且能得到这个结果的前提是运行很好
当 pattern[match[j-1]+1] != pattern[j] 时,下一个待与 pattern[j] 比较的元素下标是:match[match[j-1]]+1

KMP-5. BuildMatch的编程实现
void BuildMatch(char *pattern, int *match) {
int i, j;
int m = strlen(pattern); // 复杂度O(m)
match[0] = -1; // 初始化
for (j = 1; j < m; j++) { // 复杂度O(m)
i = match[j - 1]; // 获取前一个match值
while ((i >= 0) && (pattern[i + 1] != pattern[j])) // 检查条件
i = match[i]; // 回退
if (pattern[i + 1] == pattern[j])
match[j] = i + 1; // 更新match值
else
match[j] = -1; // 无匹配
}
}
整个算法复杂度:

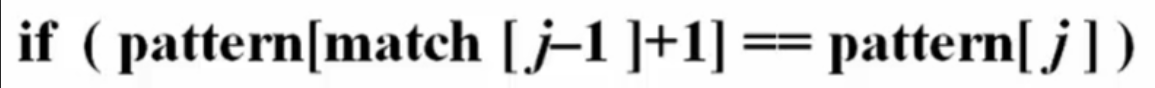







![[数据库实验一]数据库和表](https://i-blog.csdnimg.cn/direct/777e5f25bff14140970611a3db93f9f8.png)