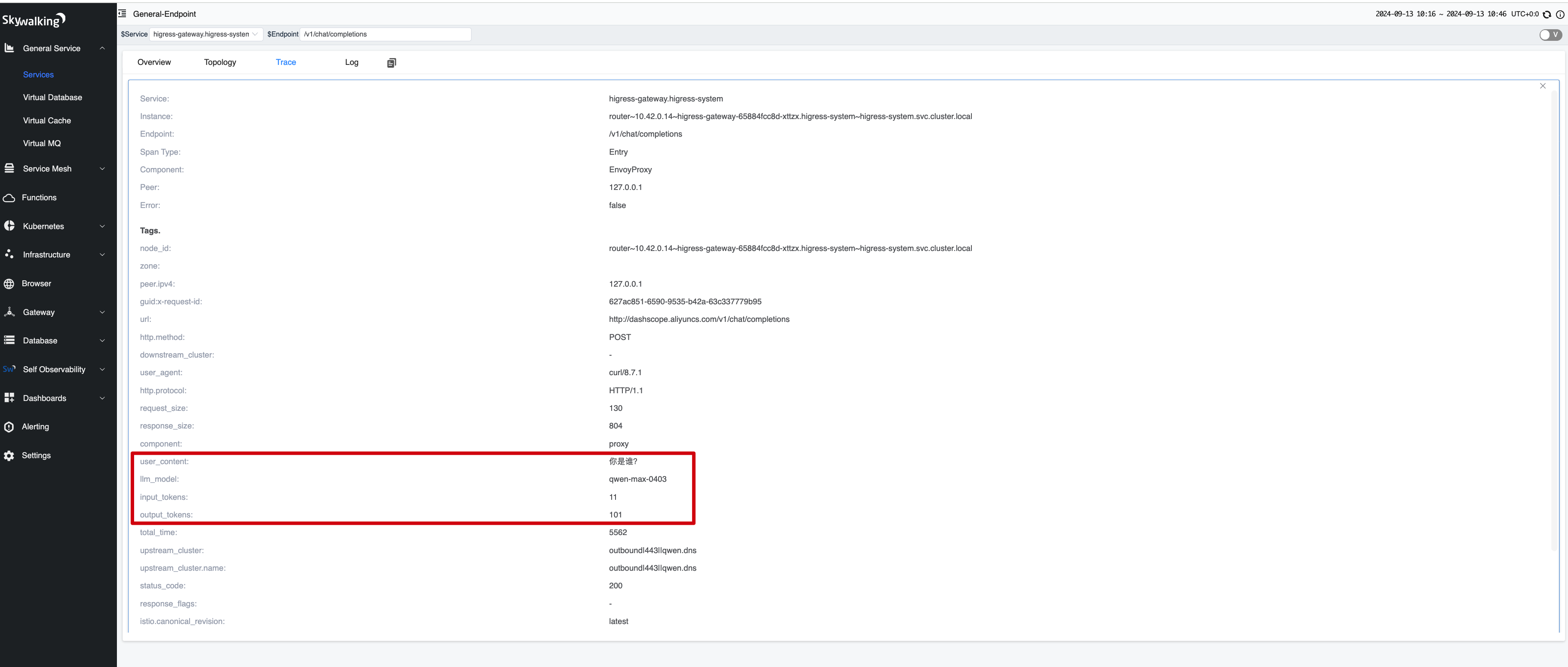
本文学习于TI 高精度实验室课程，深入探讨 delta-sigma 转换器中使用的数字滤波器。具体来说，本文将重点介绍数字滤波器如何引入延迟，因为这是 SAR 和 delta-sigma ADC 之间的显著差异。

---

---

一、低延迟数字滤波器

首先回顾一下 delta-sigma 调制器的输出和数字滤波器的必要性。然后，我们将比较和对比与 delta-sigma 转换器一起使用的不同类型的数字滤波器。上一篇文章（SAR 型 ADC 和 ΔΣ 型 ADC 的基本运行原理）解释了 delta-sigma 调制器可以调整量化噪声，也就是说，它可以最大限度地减少感兴趣信号附近的噪声，如下图所示。

为了消除较高频率下的较大噪声，需要使用低通数字滤波器。滤波器的截止频率和阶数将影响滤波器抑制的噪声量。可以使用低截止频率或具有陡峭衰减的高阶滤波器来最大限度地降低总噪声。用于此目的的滤波器一般分为两类：低延迟和高延迟。下图对比了低延迟和高延迟滤波器。延迟定义为输入信号施加到 ADC 输出稳定之间的延迟。 sinc 滤波器是一种典型的低延迟滤波器。这种滤波器通常用于数十赫兹到几千赫兹的低频输入信号。 一般，将使用低延迟滤波器的 ADC 称为 DC 优化型 ADC。

平坦通带滤波器（Flat Passband Filter）是一种高延迟滤波器。这种滤波器用于宽带宽 delta-sigma 系统。这些宽带宽 delta-sigma ADC 可以实现数十兆赫的采样率。让我们仔细看看低延迟滤波器。

低延迟滤波器是一种非常简单的滤波器，使用一些基本的数学函数（如平均值）实现。一种常见的低延迟滤波器是 sinc 滤波器。低延迟滤波器的主要优势之一是，与高延迟滤波器相比，延迟或数字稳定时间导致的延迟较短。

另一个优点是，这种类型的滤波器比更复杂的高延迟滤波器更简单、更容易实现。这意味着它占用的硅面积更小，因此成本更低。此外，简单的实现往往也会消耗更少的功率。

滤波器阶数影响滤波器曲线的下降幅度有多陡。如下图所示，五阶滤波器的下降速度比一阶滤波器快。对于这种滤波器，阶数还将影响延迟，因此 sinc 1 具有一个转换周期的延迟，而 sinc 3 具有三个转换周期的延迟。

另外注意，sinc 滤波器的陷波发生在数据速率的倍数处。上图中，可以看到陷波发生在数据速率的倍数处，最高可达数据速率的五倍。通过调整数据速率频率，可以调整这些陷波以消除某些频率，例如 50 或 60 赫兹电力线频率。这种滤波器的最后一个优点是它们非常适合直流信号，因为它们通常带宽非常有限，并且会抑制较高频率的噪声。 因此，一些直流优化的 delta-sigma 转换器具有出色的噪声性能。

这种滤波器的缺点主要在于通带在极低频率时开始下降。从这个例子可以看出，通带衰减在 0 Hz 时为 0 dB。但对于较高的频率，滤波器会立即开始衰减感兴趣的信号。 通常，对于任何交流信号，理想滤波器的通带响应应该平坦，但 sinc 滤波器的响应显然不平坦。因此，这种类型的滤波器仅限于直流和低频信号。这种滤波器的典型转换率可以从低赫兹到几千赫兹。

通过查看阻带，可以看到另一个缺点。对于低阶 sinc 滤波器，阻带衰减不是很好。 上图中可以看到 sinc 1 滤波器的阻带衰减约为 20 dB，介于数据速率的 1 到 2 倍之间。理想情况下，我们希望阻带衰减更高。好在，高阶 sinc 滤波器的阻带衰减要好得多。可以看到，对于 sinc 5 滤波器，在相同频率范围内，其衰减比 sinc 1 滤波器好 50 dB。

还有一些低延迟滤波器与 sinc 滤波器略有不同，这些滤波器类型通常称为 FIR 滤波器。FIR 的首字母缩写代表有限脉冲响应（Finite Impulse Response）。FIR 类别实际上包含许多不同的滤波器。事实上，sinc 滤波器是一种 FIR 滤波器。不过，下图中显示的滤波器类型在文献中通常被称为 FIR 滤波器，以区别于 sinc 滤波器。

从响应角度来看，这种类型的滤波器与 sinc 滤波器的区别在于，它同时在 50 和 60 赫兹处有一个陷波。 对于接收滤波器，陷波只能放置在 50 或 60 赫兹处。不过，这种类型的滤波器陷波不会像简单的 sinc 滤波器那样以规则的间隔出现。

---

二、高延迟数字滤波器

下面看看高延迟滤波器。如下图，可以看到一个典型的高延迟滤波器的示例，通常称为平坦通带滤波器。与 sinc 滤波器不同，平坦通带滤波器更像是理想的砖墙滤波器。它提供几乎平坦的通带响应，然后快速过渡到高衰减阻带。 这种类型的滤波器用于宽带宽类别的 delta-sigma 转换器。典型的转换速率可以高达数十兆赫。 例如，ADS 1610 的输出数据速率为每秒 10 兆样本。

注意，观察平坦通带滤波器时，通带的波纹非常小。底部的图放大了通带，可以看到通带中的波纹小于 0.01 db。还要注意的是，滤波器过渡非常尖锐，阻带非常低。关于此滤波器，最后要提到的一点是截止频率随数据速率而变化。上图中，可以看到滤波器截止频率设置为数据速率的约 0.5 倍。这很有用，因为此滤波器充当抗混叠滤波器并将输入信号限制为奈奎斯特频率。

这种滤波器的主要缺点是延迟时间较长。 这种滤波器的典型延迟时间可能高达 55 个转换周期。换句话说，如果将阶跃输入施加到具有这种滤波器的 ADC，则输出将无法在接下来的 55 次转换中稳定下来。对于交流正弦输入，此延迟相当于群延迟效应。稳定时的群延迟与离散 RLC 网络的情况类似。

三、导致滤波器延迟的原因

是什么原因导致了滤波器延迟？下图显示了 FIR 滤波器的典型实现。本文讨论的所有滤波器通常都使用这种拓扑结构实现。

数字滤波器由三个元件组成。延迟元件、乘法器块和求和块。整体滤波器延迟与延迟元件有关。数据一次一个转换周期地通过延迟元件，因此应用于输入的转换只有在经过所有延迟元件后才会传播到输出。因此，如果平坦通带滤波器有 55 个延迟元件，则滤波器的延迟将为 55 个转换周期。

而对于 sinc 滤波器，延迟元件的数量等于 sinc 滤波器的阶数。也就是说，三阶 sinc 滤波器将具有三个转换周期的延迟。

---

四、SAR ADC、低延迟 ΔΣ ADC 和高延迟 ΔΣ ADC 的时序示例

现在我们对延迟有了基本的了解，下面比较一下使用 SAR ADC、低延迟 delta-sigma ADC 和高延迟 delta-sigma ADC 的时序示例。以下是 sinc 1 低延迟滤波器时序示例。在此示例中，在时间 t0 处将阶跃输入施加于 ADC 输入。

注意，此步骤发生在转换周期 0 的中间。对于 sinc 1 滤波器，需要一个完整的转换周期才能稳定到阶跃输入。由于该步骤发生在转换周期的中间，因此 ADC 将需要另一个完整的周期才能稳定下来。 在图表的底部，可以看到内部模拟等效转换结果。注意，在转换周期 1 结束时，即时间 t1，内部 ADC 已完全稳定。

当转换结果已完全稳定，微控制器可以读取数据。此数据传输在图中称为读取 1（Read 1），读取在时间 t2 完成。可以使用相同的方法来显示紫色输入电压阶跃如何稳定。注意，对于 delta-sigma 转换器，数据就绪（Data Ready）用于指示转换何时完成。从时序角度来看，这是 sinc 1 低延迟滤波器的一般运行方式。

接下来看一下 sinc 3 滤波器。下图是 sinc 3 低延迟滤波器时序图。此示例与上一个示例非常相似，只是延迟是三个转换周期而不是一个。同样，在时间 t0 处（Conv 0）将阶跃输入施加于 ADC 输入。需要三个完整的转换周期才能稳定，因此内部 ADC 在转换 3 结束时稳定。一旦稳定，微控制器需要读取转换的数据。

这里要提到的一点是，时间不一定按比例计算。例如，转换周期可能需要 16 毫秒，但数据通信可能只有几微秒。这里的主要观点是说明延迟是数字滤波器的内部稳定过程，并且直到延迟之后才能从设备中检索数据。接下来，我们将针对高延迟滤波器重复该示例。

下图时序图显示了具有高延迟滤波器的 delta-sigma 转换器中的稳定过程。在此示例中，延迟为 55 个周期，因此必须放大转换进度信号的一小部分才能看到数据就绪、时钟和数据输出。

注意，在时间 t0 处将阶跃输入施加于 ADC 输入，输出几乎没有响应，直到大约 27 个周期。这大约是总延迟的一半，等于设备的群延迟。但是，一旦输出响应，在输出完全稳定之前还有另外 28 个周期。换句话说，输出将在 55 个转换周期后完全稳定。

这种响应有点类似于将阶跃输入应用于 RLC 电路，响应存在上升时间和稳定时间的延迟。这种稳定时间延迟可能看起来过多，但是，这种类型的转换器通常不会用于捕获多路复用器输出或直流瞬变。相反，这种转换器将用于捕获交流正弦信号。在这种情况下，转换器只会引入群延迟，但这种延迟的影响可能并不显著。

下面看一下使用高延迟滤波器的 delta-sigma 转换器的数据表摘录。下图显示了具有高延迟的内部平坦通带滤波器的示例设备的规格。频率响应曲线显示，在数据速率（fIN/fDATA）约为 0.5 时，从通带到阻带的过渡非常陡峭。

还要注意，阻带内的衰减相当好，在本例中低于 120 dB。该表显示了此设备的负 3 dB 带宽、稳定时间和群延迟。注意，-3 dB 点约为数据速率的一半。稳定时间与滤波器设计有关，其他转换器所需的周期数可能不同。阶跃响应显示需要 55 个周期才能完全稳定。从阶跃响应中注意到，直到大约 28 个转换周期后才会看到任何输出。然后需要剩余的 27 个周期才能完全稳定。

最后，群延迟大约是稳定时间的一半。 群延迟是施加的正弦输入和等效数字化输出之间的时间偏移。 群延迟效应在上图底部的正弦图中进行了说明。由于稳定时间中的群延迟是固定数量的转换周期，因此实际时间将随数据速率而变化。因此，对于高采样率，稳定时间中的群延迟将较低。

现在我们已经了解了使用具有低延迟和高延迟滤波器的 delta-sigma 转换器的稳定时间示例，下面看看它们与 SAR 转换器的比较。SAR 和 delta-sigma 转换器之间的一个主要区别是 SAR 具有采集阶段和转换阶段，但 delta-sigma 连续转换。考虑到这一点，模拟输入信号可以在 SAR ADC 的转换阶段转换，而不会影响采集阶段的稳定。这就是下图中时间 t0 发生的情况。在时间 t0，模拟输入发生阶跃变化。此阶跃发生在转换阶段（CNV），因此模拟输入可以在 ADC 开始采集输入信号之前完成转换。

在采集阶段（ACQ）开始时，即时间 t1，由于采样保持电容器充电，模拟输入将出现短暂的瞬态。在时间 t2，采集周期结束，并在采样保持电路中捕获模拟输入。现在转换周期（CNV）开始，采样电压被转换为数字等效值。在时间 t3，转换完成，微控制器现在可以读取数据。在 t4，数据读取完成。查看 SAR 转换器的数字通信信号，会注意到转换是由转换启动信号（CONVST）启动的。

对于 SAR，微控制器将启动转换，而对于 delta-sigma，ADC 会持续转换，并会告知微控制器转换何时完成。SAR 转换器有时被称为零延迟转换器，因为它们在捕获数据和转换可用之间的延迟最小。但实际上，所有转换器都会有一些转换延迟，并且从转换器读取转换结果也需要一些时间。

---

五、SAR ADC 与 ΔΣ ADC 的差异对比总结

下图总结了本文所描述的四种不同情况。注意，延迟最短的是 SAR 转换器，其次是带有 sinc 1 滤波器的 delta-sigma。带有平通带滤波器的 delta-sigma 在 55 个转换周期时具有最高的延迟。

注意，延迟并不总是一个关键考虑因素。例如，在音频系统中，ADC 可用于录制声音。在这种情况下，麦克风检测到声音和转换结果存储到内存之间的短暂延迟不是问题。另一方面，在安全系统中，ADC 可能正在监控需要近乎即时响应的传感器。在这种情况下，延迟可能至关重要，必须确定延迟对应用是否重要。

下图展示了 SAR 和 delta-sigma ADC 如何捕获非周期性瞬态信号。这里的关键区别在于要理解 SAR 会及时捕获瞬态信号，而 delta-sigma 会在整个时间间隔内取平均值。

在这个例子中，我们不是要考虑延迟的影响，而是要关注如何捕获数据。SAR ADC 可能会捕获一些瞬态电压尖峰，而 delta-sigma 则会对其中一些进行平均。然而，在周期性正弦波形的情况下，SAR 和 delta-sigma 都可以正确跟踪输入信号。这两个转换器之间的区别在于 delta-sigma 可能存在显著的延迟。

最后，总结一下 delta-sigma 和 SAR 架构之间的各种不同功能，如下图所示。

首先，注意 delta-sigma 可以有一个内部 PGA，而 SAR 通常有一个外部差分放大器。情况并非总是如此，但将 PGA 集成到 delta-sigma 转换器中比集成到 SAR 中更为常见。

接下来，请注意 delta-sigma 有一个主时钟输入。该时钟用于运行调制器。 在许多情况下，主时钟信号将使用内部时钟分频器。对于某些 delta-sigma 转换器，此时钟源是内部的。同时，SAR 没有主时钟输入。一些 SAR 转换器会有一个集成振荡器，用于转换周期内的计时，但 SAR 一般不需要外部振荡器。虽然 sigma 转换器会有一个集成数字滤波器，但 SAR 转换器很少提供此功能。

**SAR ADC 在不进行转换时通常消耗很少的电量，因此它们通常不需要断电控制。**另一方面，delta-sigma 转换器通常连续转换，因此断电控制通常用于使设备处于空闲状态，以便在不需要转换时最大限度地降低功耗。

最后，delta-sigma ADC 有一个数据就绪中断引脚 （DRDY），用于告知微控制器转换何时完成。通常，微控制器将使用中断或轮询方法来了解何时可以读取数据。另一方面，SAR 转换器由微控制器使用转换启动引脚 （CNVST） 明确控制。