【算法篇】二叉树类（1）（笔记）

news2024/9/28 19:35:28

目录

一、认识二叉树

1. 二叉树的种类

（1）满二叉树

（2）完全二叉树

（3）二叉搜索树

（4）平衡二叉搜索树

2. 二叉树的存储方式

3. 二叉树的遍历方式

4. 二叉树的定义

二、Leetcode 题目整理

1. 二叉树的前、中、后序遍历

（1）递归法

（2）迭代法（栈的运用）

（3）标记法（栈的运用）

2. 二叉树的层序遍历

（1）递归法

（2）迭代法

3. 翻转二叉树

（1）广度优先算法

（2）深度优先算法（前、中、后）

（3）递归法

4. 对称二叉树

（1）递归法

（2）迭代法

5. 二叉树的最大深度

6. 二叉树的最小深度

7. 平衡二叉树

8. 二叉树的所有路径

（1）回溯法

（2）迭代法

一、认识二叉树

1. 二叉树的种类

（1）满二叉树

        深度为 k，有 2^k-1 个节点的二叉树。

（2）完全二叉树

        在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。 

（3）二叉搜索树

二叉搜索树是一个有序树。

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树

（4）平衡二叉搜索树

        C++ 中 map、set、multimap，multiset 的底层实现都是 平衡二叉搜索树，所以map、set 的增删操作 时间时间复杂度 是 logn。

2. 二叉树的存储方式

        二叉树可以链式存储，也可以顺序存储。

        链式存储方式就用 指针， 顺序存储的方式就是用 数组。

        在数组存储中：如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

3. 二叉树的遍历方式

二叉树主要有两种遍历方式：

  1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
  2. 广度优先遍历：一层一层的去遍历。

从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

  • 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  • 广度优先遍历
    • 层次遍历（迭代法）

4. 二叉树的定义

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

二、Leetcode 题目整理

1. 二叉树的前、中、后序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/566103571/94. 二叉树的中序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-inorder-traversal/description/145. 二叉树的后序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-postorder-traversal/description/

        给你二叉树的根节点 root ，返回它节点值的 前序 / 中序 / 后序遍历。

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 前序遍历
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& result) {
        if (cur == NULL) return;
        result.push_back(cur->val);
        traversal(cur->left, result);
        traversal(cur->right, result);
    }

    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};


// 中序遍历
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& result) {
        if (cur == NULL) return;
        traversal(cur->left, result);
        result.push_back(cur->val);
        traversal(cur->right, result);
    }

    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};


// 后序遍历
class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& result) {
        if (cur == NULL) return;
        traversal(cur->left, result);
        traversal(cur->right, result);
        result.push_back(cur->val);
    }

    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

（2）迭代法（栈的运用）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 前序遍历
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> record;
        vector<int> result;
        if (root == NULL) return result;
        record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            result.push_back(node->val);
            if (node->right) record.push(node->right);
            if (node->left) record.push(node->left);
        }
        return result;
    }
};


// 中序遍历
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur);
                cur = cur->left;
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);
                cur = cur->right;
            }
        }
        return result;
    }
};


// 后序遍历（前序输出后翻转就可以）
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

（3）标记法（栈的运用）

        将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 前序遍历
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            if (node != nullptr) {
                record.pop();
                if (node->right) record.push(node->right);
                if (node->left) record.push(node->left);
                record.push(node);
                record.push(nullptr);
            }
            else {
                record.pop();
                node = record.top();
                record.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};


// 中序遍历
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        // 标记法
        vector<int> result;
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();  
            // 等于nullptr，说明最先处理的节点已经遍历到。叶子结点已经到底，需要打印中间节点
            // 不等于nullptr，说明还未遍历到最先处理的节点
            if (node != nullptr) {
                record.pop(); // 弹出顶部元素，避免重复
                if (node->right) record.push(node->right);
                record.push(node);
                record.push(nullptr);
                if (node->left) record.push(node->left);
            }
            else {
                record.pop(); // 弹出nullptr
                node = record.top();
                record.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};


// 后序遍历
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            if (node != nullptr) {
                // 中 nullptr 右 左
                record.push(nullptr);
                if (node->right) record.push(node->right);
                if (node->left) record.push(node->left);
            }
            else {
                record.pop();
                node = record.top();
                record.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

2. 二叉树的层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-level-order-traversal/description/

        给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

 

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：
输入：root = [1]
输出：[[1]]

示例 3：
输入：root = []
输出：[]

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        // 二叉树的层级是递增的（从根节点开始，逐层向下），且每个层级只会在第一次遇到时执行这行代码
        // 因此每个层级只会被添加一次对应的 vector<int>()
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        queue<TreeNode*> que;
        if (root != nullptr) que.push(root);
        while (!que.empty()) {
            // 现在que队列中的元素为当前层的节点个数
            int size = que.size();
            vector<int> record;
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                record.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(record);
        }
        return result;
    }
};

3. 翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/invert-binary-tree/description/

        给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：
输入：root = []
输出：[]

        想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。 

（1）广度优先算法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 层序遍历
        if (!root || (!root->left && !root->right)) return root;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();

                swap(node->left, node->right);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

（2）深度优先算法（前、中、后）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 后序遍历（循环法）
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                // 栈顶元素不等于 nullptr
                record.push(node);                          // 中 
                record.push(nullptr);   // 到遍历中节点的时候停一下，需要先遍历右节点
                if (node->right) record.push(node->right);  // 右
                if (node->left) record.push(node->left);    // 左
            }
            else {
                node = record.top();
                record.pop();
                swap(node->left, node->right);
            }
        }
        return root;
    }
};


class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 中序遍历（循环法）
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                // 栈顶元素不等于 nullptr
                if (node->right) record.push(node->right);  // 右
                record.push(node);                          // 中 
                record.push(nullptr);   // 遍历完左节点的时候停一下，现处理中节点
                if (node->left) record.push(node->left);    // 左
            }
            else {
                node = record.top();
                record.pop();
                swap(node->left, node->right);
            }
        }
        return root;
    }
};


class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 前序遍历（循环法）
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                // 栈顶元素不等于 nullptr
                if (node->right) record.push(node->right);  // 右
                if (node->left) record.push(node->left);    // 左
                record.push(node);                          // 中   
                record.push(nullptr);
            }
            else {
                node = record.top();
                record.pop();
                swap(node->left, node->right);
            }
        }
        return root;
    }
};

（3）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
};

4. 对称二叉树

101. 对称二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/symmetric-tree/description/

        给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：
输入：root = [1,2,2,3,4,4,3]
输出：true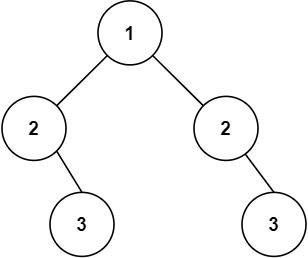

示例 2：
​​​​​​​输入：root = [1,2,2,null,3,null,3]
输出：false

（1）递归法

① 终止条件

  • 左节点为空，右节点不为空，不对称，return false
  • 左不为空，右为空，不对称 return false
  • 左右都为空，对称，返回true

② 单层递归的逻辑

         单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

  • 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
  • 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
  • 如果左右都对称就返回 true ，有一侧不对称就返回 false 。
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        // 判断条件
        if (left == nullptr && right != nullptr) return false;
        else if (left != nullptr && right == nullptr) return false;
        else if (left == nullptr && right == nullptr) return true;
        else if (left->val != right->val) return false;

        bool outside = compare(left->left, right->right);   // 外层判断
        bool inside = compare(left->right, right->left);    // 内层判断
        return (outside && inside);
    }

    bool isSymmetric(TreeNode* root) {
        // 递归法
        if (root == nullptr) return true;
        return compare(root->left, root->right);
    }
};

（2）迭代法

        通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while (!que.empty()) {
            TreeNode* leftnode = que.front(); que.pop();
            TreeNode* rightnode = que.front(); que.pop();

            if (leftnode == nullptr && rightnode != nullptr) return false;
            else if (leftnode != nullptr && rightnode == nullptr) return false;
            else if (leftnode == nullptr && rightnode == nullptr) continue;
            else if (leftnode->val != rightnode->val) return false;

            // 填入数据
            que.push(leftnode->left);
            que.push(rightnode->right);
            que.push(leftnode->right);
            que.push(rightnode->left);
        }
        return true;
    }
};

5. 二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/maximum-depth-of-binary-tree/description/

        给定一个二叉树 root ，返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：
输入：root = [1,null,2]
输出：2
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        // 二叉树层序遍历
        queue<TreeNode*> que;
        int depth = 0;
        if (root == NULL) return depth;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

6. 二叉树的最小深度

111. 二叉树的最小深度 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/minimum-depth-of-binary-tree/description/

        给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

        说明：叶子节点是指没有子节点的节点。

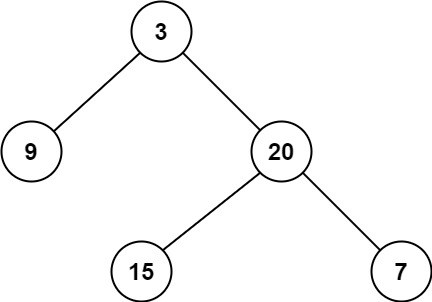
示例 1：
​​​​​​​输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        // 层序遍历
        int depth = 0;
        queue<TreeNode*> que;
        if (root == NULL) return 0;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
            }
        }
        return depth;
    }
};

7. 平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/balanced-binary-tree/description/

        给定一个二叉树，判断它是否是 平衡二叉树。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：true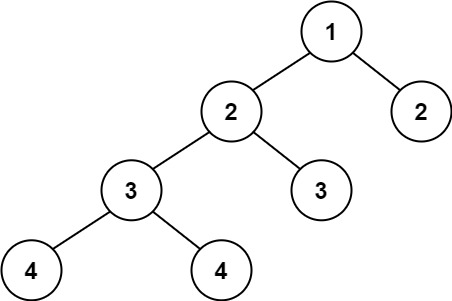

示例 2：
​​​​​​​输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
示例 3：
输入：root = []
输出：true

  思路：

（1）明确递归函数的参数 和 返回值

        参数：当前传入节点。         返回值：以当前传入节点为根节点的树的高度。

        如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。

（2）明确终止条件

        递归的过程中 依然是遇到 空节点了为终止，返回 0，表示 当前节点为 根节点的 树高度为0。

（3）明确单层递归的逻辑

        分别求出其左右子树的高度，然后如果差值小于 等于1，则返回当前二叉树的高度，否则返回-1，表示已经 不是二叉平衡树了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getHeight(TreeNode* node) {     // 后序遍历
        if (node == nullptr) return 0;

        int leftNum = getHeight(node->left);
        if (leftNum == -1) return -1;
        int rightNum = getHeight(node->right);
        if (rightNum == -1) return -1;

        // 子树拥有的层数越多，高度越高
        return abs(leftNum - rightNum) > 1 ? -1 : 1 + max(leftNum, rightNum);
    }

    bool isBalanced(TreeNode* root) {
        // 回溯法
        return getHeight(root) == -1 ? false : true;
    }
};

8. 二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）icon-default.png?t=O83Ahttps://leetcode.cn/problems/binary-tree-paths/description/

        给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。

示例 1：
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：
输入：root = [1]
输出：["1"]

（1）回溯法

        这道题目要求 从根节点到叶子的路径，所以需要 前序遍历，这样才 方便让父节点 指向孩子 节点，找到 对应的路径。我们 要把路径 记录下来，需要 回溯来回退一个 路径 再进入另一个路径。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void TreePath(TreeNode* node, vector<string>& path, string str) {
        str = str + to_string(node->val);
        if (!node->left && !node->right) {
            path.push_back(str);
            return;
        }
        if (node->left) TreePath(node->left, path, str + "->");
        if (node->right) TreePath(node->right, path, str + "->");
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        // 前序遍历
        vector<string> result;
        if (root == nullptr) return result;
        TreePath(root, result, "");
        return result;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*> treeSt;// 保存树的遍历节点
        stack<string> pathSt;   // 保存遍历路径的节点
        vector<string> result;  // 保存最终路径集合
        if (root == NULL) return result;
        treeSt.push(root);
        pathSt.push(to_string(root->val));
        while (!treeSt.empty()) {
            TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
            string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径
            if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
                result.push_back(path);
            }
            if (node->right) { // 右
                treeSt.push(node->right);
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            if (node->left) { // 左
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        return result;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2168230.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

(done) 使用泰勒展开证明欧拉公式

(done) 使用泰勒展开证明欧拉公式

问问神奇的 GPT&#xff0c;how to prove euler formula? 一个答案如下&#xff1a;
阅读更多...
华硕NUC亮相工博会，解锁工业AI PC解决方案

华硕NUC亮相工博会，解锁工业AI PC解决方案

2024年9月24日至28日&#xff0c;中国国际工业博览会于上海国家会展中心盛大举行&#xff0c;华硕智能物联网展台位于展馆6.1H E183展位&#xff0c;在展位上华硕向大众展示了智能AI、物联网设备、华硕NUC等解决方案及IoT硬件产品&#xff0c;吸引了众多专业观众驻足交流和体验…
阅读更多...
线程池的执行流程和配置参数总结

线程池的执行流程和配置参数总结

一、线程池的执行流程总结 提交线程任务&#xff1b;如果线程池中存在空闲线程&#xff0c;则分配一个空闲线程给任务&#xff0c;执行线程任务&#xff1b;线程池中不存在空闲线程&#xff0c;则线程池会判断当前线程数是否超过核心线程数&#xff08;corePoolSize&#xff09…
阅读更多...
EfficientViT(2023CVPR)：具有级联组注意力的内存高效视觉Transformer!

EfficientViT(2023CVPR)：具有级联组注意力的内存高效视觉Transformer!

EfficientViT: Memory Efficient Vision Transformer with Cascaded Group Attention EfficientViT: 具有级联组注意力的内存高效视觉Transformer 万文长字&#xff0c;请耐心观看~ 论文地址&#xff1a; https://arxiv.org/abs/2305.07027 代码地址&#xff1a; Cream/Effici…
阅读更多...
计算机毕业设计 饮食营养管理信息系统的设计与实现 Java实战项目 附源码+文档+视频讲解

计算机毕业设计 饮食营养管理信息系统的设计与实现 Java实战项目 附源码+文档+视频讲解

博主介绍&#xff1a;✌从事软件开发10年之余&#xff0c;专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ &#x1f345;文末获取源码联系&#x1f345; &#x1f447;&#x1f3fb; 精…
阅读更多...
《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch9 策略梯度方法 -9.3.1

《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch9 策略梯度方法 -9.3.1

之前看了 2 次视频&#xff0c;公式有点多&#xff0c; 还是没整理出来。 这个版本是以下步骤后的版本 基本把相关的核心论文过了一遍&#xff0c;代码整理了部分 PDF 资料 整理 v3 链接 视频 链接 习题 策略梯度方法需要估计值 函数近似&#xff1a; 状态/动作 价值、策略 参…
阅读更多...
C++初阶：STL详解（四）——vector迭代器失效问题

C++初阶：STL详解（四）——vector迭代器失效问题

✨✨小新课堂开课了&#xff0c;欢迎欢迎~✨✨ &#x1f388;&#x1f388;养成好习惯&#xff0c;先赞后看哦~&#x1f388;&#x1f388; 所属专栏&#xff1a;C&#xff1a;由浅入深篇 小新的主页&#xff1a;编程版小新-CSDN博客 一&#xff1a;迭代器失效的本质 迭代器的主…
阅读更多...
VulnStack-红日靶机（二）

VulnStack-红日靶机（二）

红日靶机二 环境搭建 只需要把虚拟机的 host-only&#xff08;仅主机&#xff09;网卡改为 10.10.10.0 网段&#xff0c;如下配置 把 NAT 网卡&#xff0c;改为 192.168.96.0 网段&#xff0c;如下 首先恢复到 v1.3 快照 让后点击放弃&#xff0c;放弃后再开机&#xff0c;用…
阅读更多...
Shopify独立站运营必知必会：选品与防封技巧

Shopify独立站运营必知必会：选品与防封技巧

独立站和第三方平台是目前最常见的跨境电商销售模式&#xff0c;相比于第三方平台&#xff0c;独立站的商家可以自己建站&#xff0c;自行决定运营模式和营销手段等策略&#xff0c;尤其是在准入门槛上&#xff0c;难度会更低&#xff0c;这些特点吸引了不少商家选择独立站开店…
阅读更多...
电动车、电单车入梯数据集电动车进电梯检测识别(代码+教程+数据集)

电动车、电单车入梯数据集电动车进电梯检测识别(代码+教程+数据集)

数据集介绍 共有 5347 张图像和一一对应的标注文件 标注文件格式提供了两种&#xff0c;包括VOC格式的xml文件和YOLO格式的txt文件。 标注的对象共有以下几种&#xff1a; [‘Electric-bicycle’] 标注框的数量信息如下&#xff1a;&#xff08;标注时一般是用英文标的&am…
阅读更多...
使用shardingsphere实现mysql数据库分片

使用shardingsphere实现mysql数据库分片

在大数据时代&#xff0c;随着业务数据量的不断增长&#xff0c;单一的数据库往往难以承载大规模的数据处理需求。数据库分片&#xff08;Sharding&#xff09;是一种有效的数据库扩展技术&#xff0c;通过将数据分布到多个数据库实例上&#xff0c;提高系统的性能和可扩展性。…
阅读更多...
图解Lamda使用场景

图解Lamda使用场景

1.参考如下文章&#xff0c;讲的挺好的 深入浅出 C Lambda表达式&#xff1a;语法、特点和应用 &#xff08;请注意&#xff1a;此链接是本章节的原文&#xff09; 2. 什么是 Lambda表达式&#xff08;截取以上参考文章&#xff09; Lambda表达式是一种在被调用的位置或作为…
阅读更多...
每日OJ题_牛客_NC40链表相加（二）_链表+高精度加法_C++_Java

每日OJ题_牛客_NC40链表相加（二）_链表+高精度加法_C++_Java

目录 牛客_NC40链表相加&#xff08;二&#xff09;_链表高精度加法 题目解析 C代码 Java代码 牛客_NC40链表相加&#xff08;二&#xff09;_链表高精度加法 链表相加(二)_牛客题霸_牛客网 题目解析 模拟⾼精度加法的过程&#xff0c;只不过是在链表中模拟。 C代码 /*…
阅读更多...
107.WEB渗透测试-信息收集-FOFA语法（7）

107.WEB渗透测试-信息收集-FOFA语法（7）

免责声明&#xff1a;内容仅供学习参考&#xff0c;请合法利用知识&#xff0c;禁止进行违法犯罪活动&#xff01; 内容参考于&#xff1a; 易锦网校会员专享课 上一个内容&#xff1a;106.WEB渗透测试-信息收集-FOFA语法&#xff08;6&#xff09; 密码文件&#xff1a; 语…
阅读更多...
MFC设置特定控件字体大小和背景颜色

MFC设置特定控件字体大小和背景颜色

MFC设置特定控件字体大小和背景颜色 初始化函数里 m_editFont.CreatePointFont(580 , _T("宋体"));m_ctrlEdit.SetFont(&m_editFont);重写消息 HBRUSH CMFCTESTDlg::OnCtlColor(CDC* pDC, CWnd* pWnd, UINT nCtlColor) {HBRUSH hbr CDialogEx::OnCtlColor(pDC,…
阅读更多...
Calcite第一课

Calcite第一课

Calcite 是什么&#xff1f; 2024 年 9 月&#xff0c;最新版本 1.37.0 。前面三节我们先不看任何的源码&#xff0c;只从背景、介绍、概念、原理层面入手&#xff0c;作为深入学习和源码分析的预备。 如果用一句话形容 Calcite&#xff0c;Calcite 是一个用于优化异构数据源的…
阅读更多...
最全测评！分享7款超好用的AI论文润色网站

最全测评！分享7款超好用的AI论文润色网站

在当前的学术写作领域&#xff0c;AI论文润色工具已经成为提升论文质量和效率的重要助手。以下是七款超好用的AI论文润色网站&#xff0c;其中特别推荐千笔-AIPassPaper。 一、千笔-AIPassPaper 是一款集论文大纲生成、内容填充、文献引用、查重修改于一体的全方位论文写作平…
阅读更多...
友思特“未来视界”趣味实验室 | 第2讲：中草药的高光谱成像

友思特“未来视界”趣味实验室 | 第2讲：中草药的高光谱成像

第2讲 ——当中药遇上高光谱系统 友思特“未来视界”实验室第二讲开课了&#xff01;本期主角是凝结了中国古老智慧的特色——中药。 从神农尝百草到《本草纲目》典籍问世&#xff0c;中药材发展至今&#xff0c;品类已高达上万种。在这其中&#xff0c;难免会存在形态相似而…
阅读更多...
曲面构件的布尔运算

曲面构件的布尔运算

1.前言 布尔运算算法有多种&#xff0c;可以根据几何数据表达方式分为Brep布尔运算、CSG布尔运算、网格布尔运算等&#xff0c;而网格布尔运算又又多种&#xff0c;如BSP方式、八叉树方式&#xff0c;博主实现过Brep布尔运算、BSP和八叉树两种网格布尔运算。详细可参考博主文章…
阅读更多...
[NewStarCTF 2023 公开赛道]Begin of PHP1

[NewStarCTF 2023 公开赛道]Begin of PHP1

开始代码审计. <?php error_reporting(0); highlight_file(__FILE__);if(isset($_GET[key1]) && isset($_GET[key2])){echo "Level 1<br>";if($_GET[key1] ! $_GET[key2] && md5($_GET[key1]) md5($_GET[key2])){$flag1 True;}else{die(…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023