整数在内存中的存储（c语言）

news2024/9/27 21:28:57

1.原码反码补码（以及他们之间的转换）

当一个数为正数的时候，不存在原码反码补码的差别，也就是一样的；

当一个数为负数的时候，以-1为例子，对这个过程进行讲解。

1000 0000 0000 0000 0000 0000 0000 0001 原码（实际我们看到的）

1111 1111 1111 1111 1111 1111 1111 1110 反码，（符号位不变也就是最左边的那个，其余的把原码中为0的变为1，1的变为0）

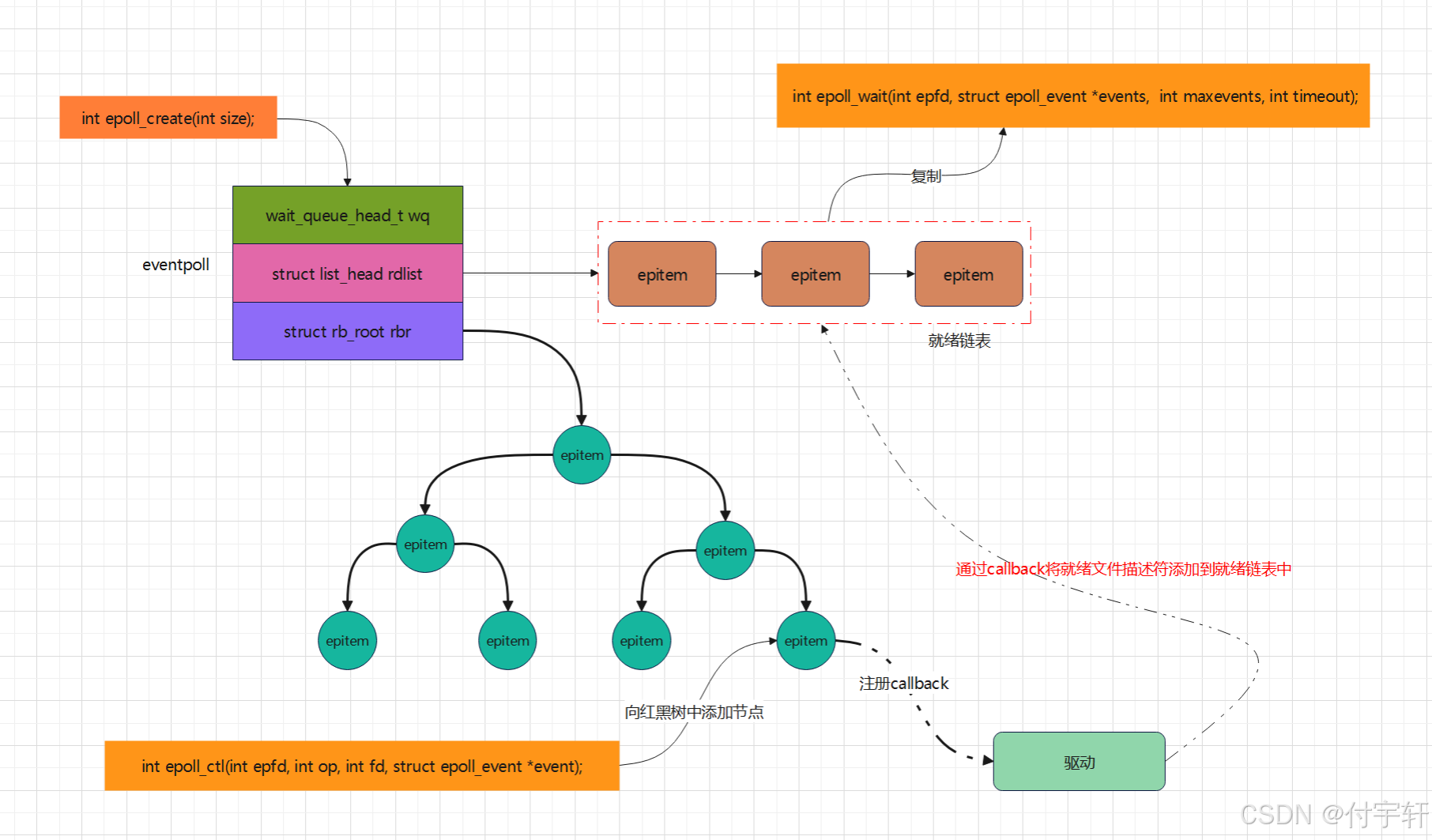
1111 1111 1111 1111 1111 1111 1111 1111 补码=反码+1 （补码也就是计算机中存储和表示的形式，通过这样存储后去进行计算能解决原码没办法进行负数计算的弊端，也能解决跨0运算的问题（会算两次0））（别人的图，这个图描述了如果只进行取反码会出现的漏洞）

当要转换回去的时候，先对补码 -1 得到反码，再变0为1，变1为0。

2.对几个例题进行解析

2.1

char a=-1;

signed char a1 = -1;

unsigned char a2=-1;

printf("%d %d %d",a,a1,a2);

由上面的举例已经知道 -1的补码是

1111 1111 1111 1111 1111 1111 1111 1111

但是因为是char 所以会发生截断，最后保留的就是1111 1111；%d打印的是有符号的整型（需要进行整型提升，并打印出原码），因为char 和signed char（在vs上）是一样的，都是补符号位，既仍然是 1111 1111 1111 1111 1111 1111 1111 1111 ，所以都仍然是为-1；但是unsigned char是无符号整型，高位是补0的，所以就变为了0000 0000 0000 0000 0000 0000 1111 1111，也就是255；

2.2

char a=-128;

printf("%u",a);

1000 0000 0000 0000 0000 0000 1000 0000

1111 1111 1111 1111 1111 1111 0111 1111

1111 1111 1111 1111 1111 1111 1000 0000

一开始还是一样发生截断，剩下的是1000 0000（在内存中）由于要发生整数提升，他又是有符号的char，所以整型提升后就是上面的补码；

%u打印的是无符号的整型（同样需要进行整型提升）但是没有了原反补的概念，所以直接现在的补码就是原码，最终打印的就是1111 1111 1111 1111 1111 1111 1000 0000，不再需要转换为原码；

2.3

char a=128;

printf("%u",a);

当a为128，跟2.2同样的过程，你会发现128和-128用 %u打印的时候结果都是一样的；