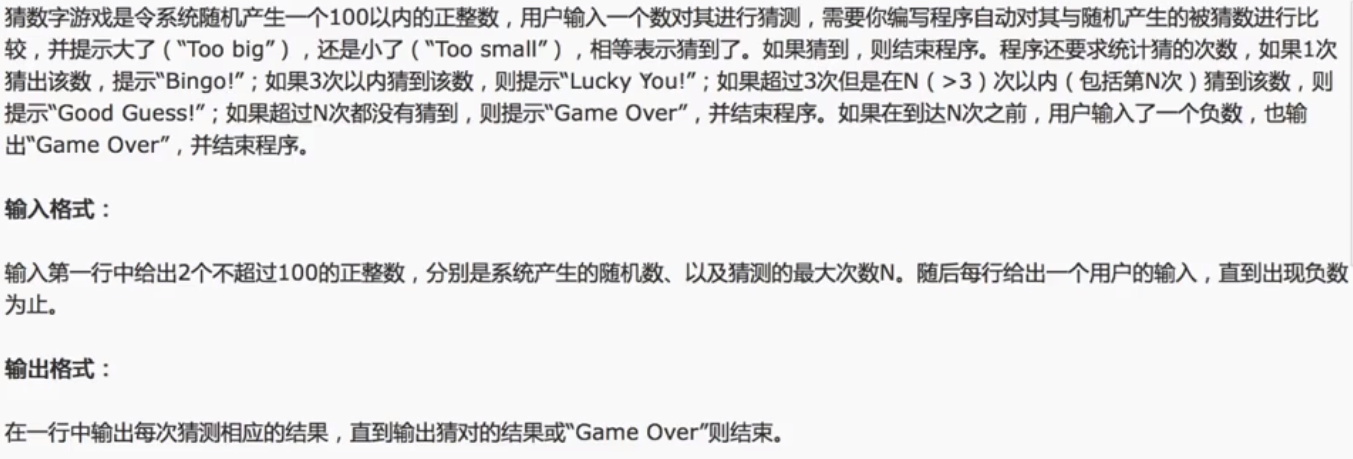
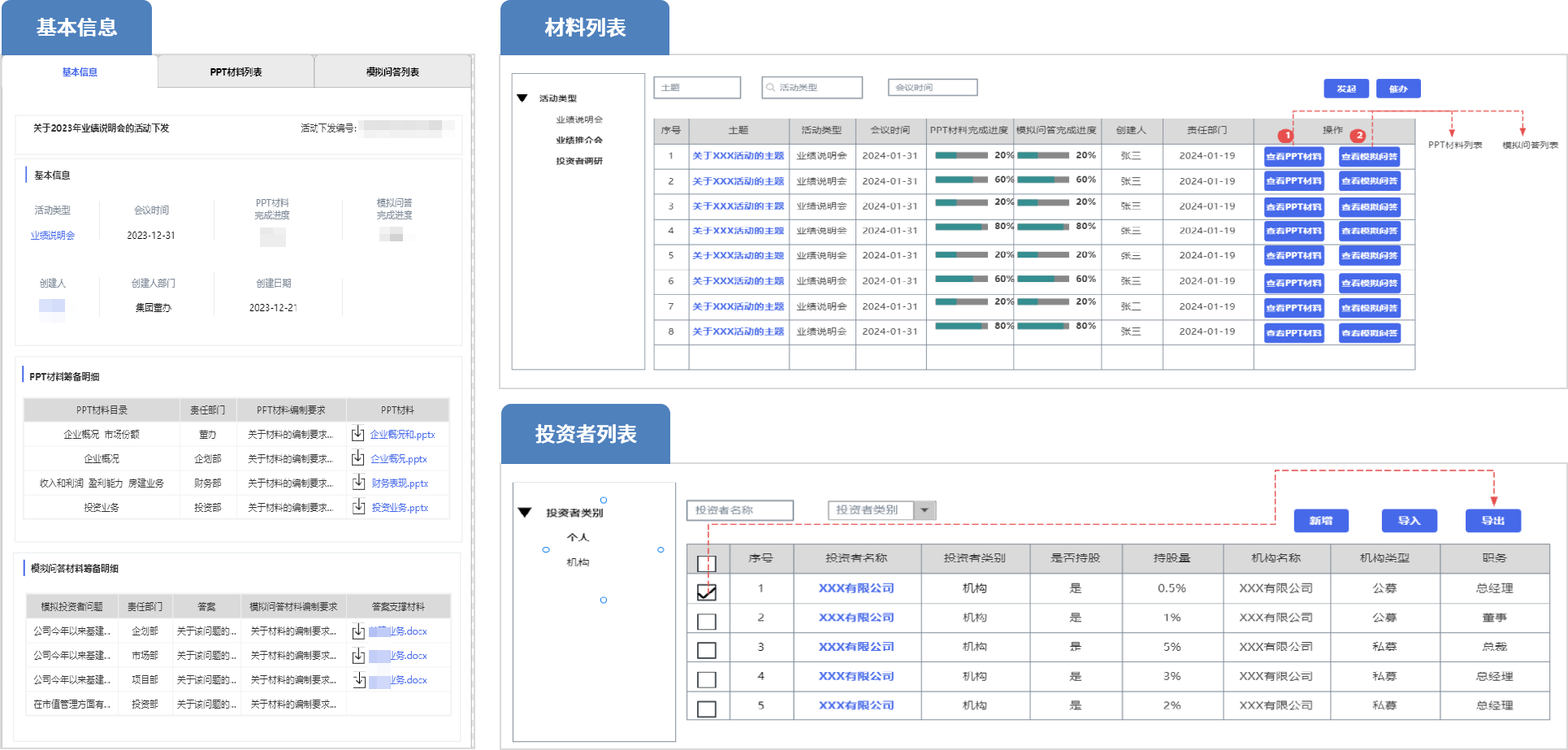
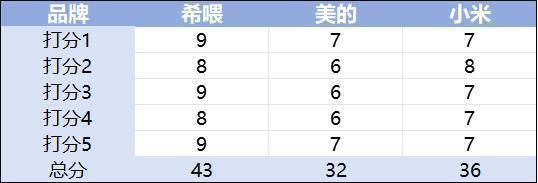
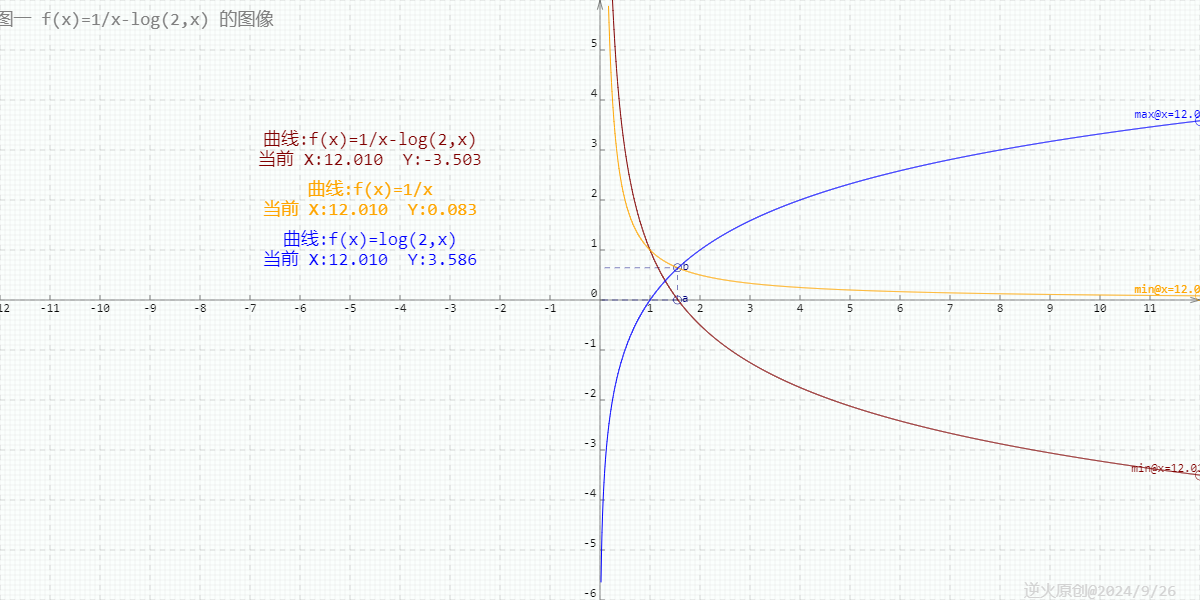
要想在前端页面中展示本地文件或者文件夹，需要使用convertfilesrc这个api，可以非常方便的展示内容，官方文档：tauri | Tauri Apps

convertFileSrc甚至位于invoke之前，但我却一直没有注意到它，一方面是因为，之前从没有想过要使用绝对路径来转换URL，因为纯前端是做不到这一点的；另一方面，由于思维惯性，前端打开本地文件往往都是用的input file，遇到这个问题我一直想的是如何从input事件着手，没有去仔细看文档……这就是所谓的灯下黑吗

需要选择文件并拿到文件路径，然后传递进去，选择文件就需要使用dialog的api，需要配置：

"dialog": {
                "all": true,
                "ask": true,
                "confirm": true,
                "message": true,
                "open": true,
                "save": true
            },

点击一个按钮来选择文件触发的事件，拿到选中的文件路径，然后转化为url：

import { convertFileSrc } from '@tauri-apps/api/tauri'
import { open } from '@tauri-apps/api/dialog'


const localImagePath = ref('')

const uploadIcon = async () => {
    console.log('uploadIcon')
    const selected = await open({
        multiple: false, // 只允许选择一个文件
        filters: [
            {
                name: 'Image',
                extensions: ['png', 'jpg', 'jpeg', 'gif'],
            },
        ],
    })

    if (selected) {
        console.log('Selected file path:', selected)
        const url = convertFileSrc(selected as string)
        localImagePath.value = url
        return selected // 返回选择的文件路径
    }
}

然后展示的时候使用img标签就可以了：

最后的效果：