个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创前缀和(4)_除自身以外数组的乘积
收录于专栏【经典算法练习】
本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
1. 题目链接 :
2. 题目描述 :
3. 解法(一维前缀和) :
算法思路 :
代码展示 :
进阶:
结果分析 :
1. 题目链接 :
OJ链接: 除自身以外数组的乘积
2. 题目描述 :
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4] 输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
3. 解法(一维前缀和) :
算法思路 :
注意题目的要求,不能使用除法,并且在O(N)的时间复杂度内完成该题.那么我们就不能使用暴力的解法,以及求出整个数组的乘积,然后除以单个元素的方法.
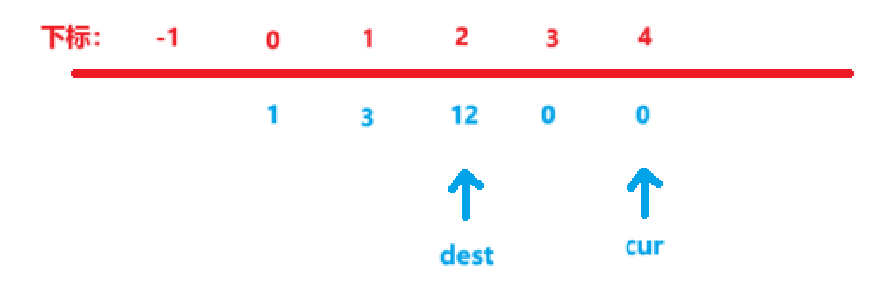
继续分析,根据题意,对于每一个位置的最终结果ret[i],它是由两部分组成的:
1. nums[0] * nums[1] * ......* nums[i - 1]
2. nums[i + 1] * nums[1 + 2] * ...... * nums[n - 1]
于是,我们可以利用前缀和思想,使用两个数组pos和suf,分别处理出来两个信息:
1. post表示: i位置之前的所有元素,即[0, i - 1]区间内所有元素的前缀乘积
2. suf表示: i位置之后的所有元素,即[i + 1, n - 1]区间内所有元素的后缀乘积,然后处理最终结果
代码展示 :
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> front_dp(n), back_dp(n);
front_dp[0] = 1;
back_dp[n - 1] = 1;
for(int i = 1; i < n; i++)
front_dp[i] = front_dp[i - 1] * nums[i - 1];
for(int i = n - 2; i >= 0; i--)
back_dp[i] = back_dp[i + 1] * nums[i + 1];
vector<int> ret;
for(int i = 0; i < n; i++)
ret.push_back(front_dp[i] * back_dp[i]);
return ret;
}
};
进阶:
你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> ret(n, 1);
//计算前缀和
for(int i = 1; i < n; i++)
ret[i] = ret[i - 1] * nums[i - 1];
//计算后缀乘积与前缀乘积相乘
int flag = 1;
for(int i = n - 1; i >= 0; i--)
{
ret[i] *= flag;
flag *= nums[i];
}
return ret;
}
};
结果分析 :
优化说明
- 使用一个结果数组: 直接在
ret数组中计算前缀乘积,后续再用一个变量suffix计算后缀乘积并更新ret。- 空间复杂度: 最终的空间复杂度变为 O(1)(输出数组不算额外空间),因为我们只使用了一个额外的变量
suffix来存储后缀乘积。