全文链接:https://tecdat.cn/?p=37759
分析师:Anting Li
本文将深入探讨逻辑回归在心脏病预测中的应用与优化。通过对加州大学欧文分校提供的心脏病数据集进行分析,我们将揭示逻辑回归模型的原理、实现过程以及其在实际应用中的优势和不足。同时,我们还将介绍多种优化方法,如牛顿迭代、随机梯度下降和贝叶斯逻辑回归等,以提高模型的性能和准确性(点击文末“阅读原文”获取完整代码数据)。
此外,本文还将结合代码和数据探讨非参数化的自助重采样方法在逻辑回归中的应用及模型差异分析。通过对不同计算逻辑回归参数抽样分布方法的比较,我们将深入了解这些方法的假设和适用场景,为实际应用中选择合适的方法提供参考。
逻辑回归在心脏病预测中的应用与优化
本视频教程聚焦于逻辑回归这一广泛应用的分析模型,旨在处理因变量二元分类问题。
视频
逻辑回归在传统线性回归基础上引入 sigmoid 函数,通过假设数据服从特定分布并运用极大似然估计进行参数估计。在众多领域如金融、医学、市场营销和网络安全中,逻辑回归都有着重要应用。
关键词:逻辑回归;心脏病预测;数据清洗;模型优化;模型评价
一、引言
逻辑回归作为一种经典的统计学习方法,在二元分类问题中发挥着重要作用。本文以心脏病数据集为研究对象,深入探讨逻辑回归模型的原理、实现过程、优化策略以及评价指标。
二、逻辑回归模型原理
(一)模型主体
逻辑回归假定观测的 y 服从伯努利分布,通过将线性回归的结果输入 sigmoid 函数,将输出值映射到 0 到 1 之间,代表事件发生的概率。即 logit (P (Y = 1)) = β₀ + β₁_X₁ + …… + βₖ_Xₖ,其中 P = g (β₀ + β₁X₁ +... + βₖXₖ),g (X) = 1 / (1 + e⁻ˣ)。
(二)对数似然函数
逻辑回归的对数似然函数为 L = log [∏₁ᵢ₌₁ⁿ pᵢʸⁱ(1 - pᵢ)¹⁻ʸⁱ] = ∑₁ᵢ₌₁ⁿ[yᵢlog (pᵢ) + (1 - yᵢ) log (1 - pᵢ)] = ∑₁ᵢ₌₁ⁿ[yᵢβₜXᵢ - log (1 + e⁽ᵦₜˣᵢ⁾)],通过最大化这个对数似然函数来估计模型参数。
三、模型实现
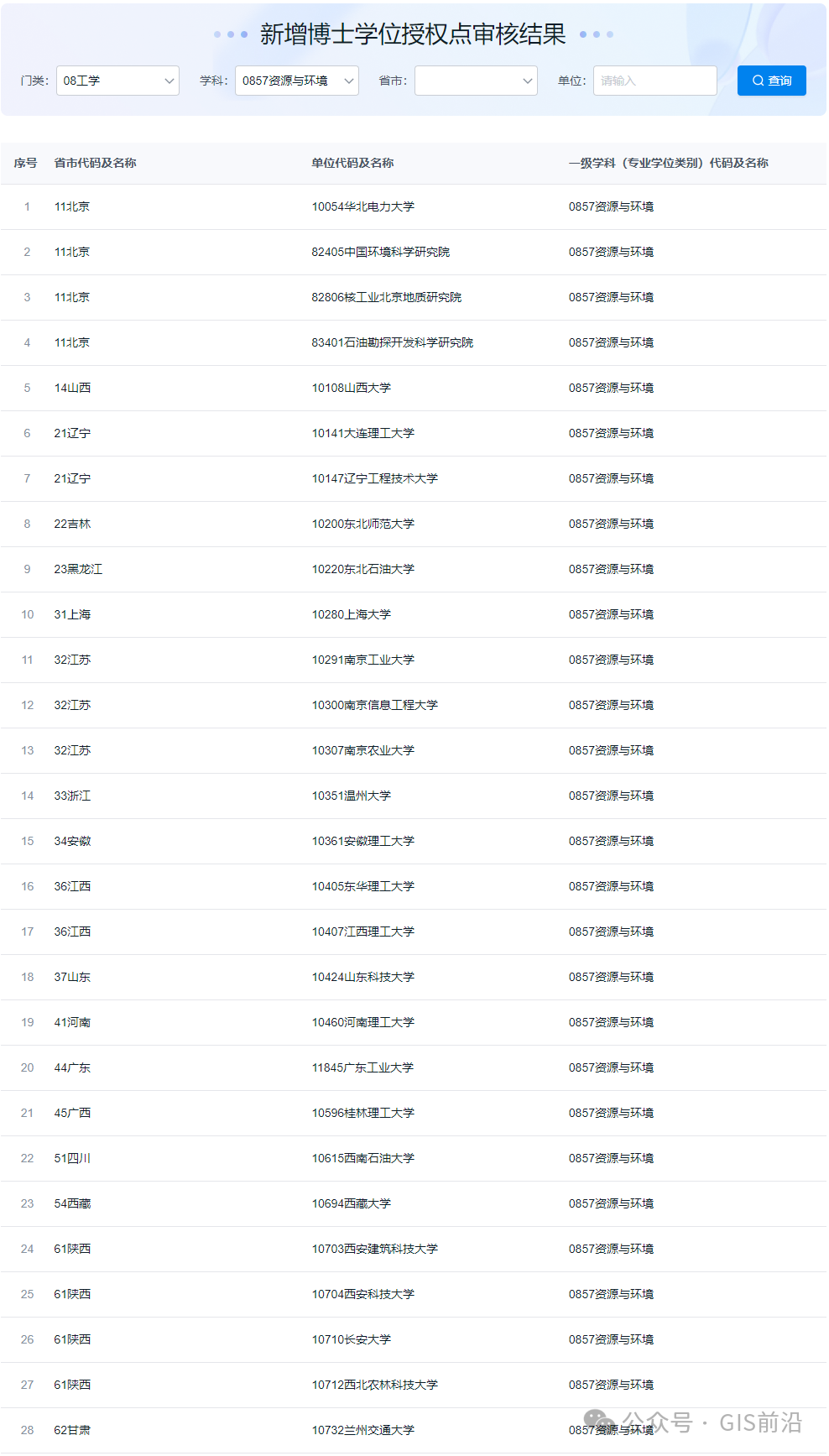
(一)数据集介绍
选用的心脏病数据集由加州大学欧文分校(UCI)提供,是一个开放性的数据集,包含 303 个样本,每个样本具有 14 个不同的特征指标,如年龄、性别、胸痛类型、血压、最高心率、ST 段抬高等。
(二)数据清洗
对数据进行缺失值和异常值处理,得到 297 条可用数据。
进行标准化处理,消除不同特征之间的量纲差异。
将处理后的数据划分为训练集(前 70%)和测试集(后 30%)。
(三)模型建立
选择相关系数最高的两个连续型自变量 thalach 和 oldpeak,针对心脏病发病情况二分类变量 target 构建逻辑回归模型进行分析和预测。使用 R 语言的 glm 函数,令 link = "logit"。
四、模型结果
thalach 和 oldpeak 在连续型变量中的相关系数最高,均大于 0.4。
模型中的自变量均显著。
模型的 AUC 值为 0.79,显示出良好的拟合效果。
五、模型优化
为提升模型性能,采用了以下优化方法:
(一)牛顿迭代
得到新的参数 Beta₀ₑ、Beta₁ₑ、Beta₂ₑ,准确性为 0.719101123595506,迭代次数为 5 次。
(二)随机梯度下降
得到新的参数 Beta₀ₑ、Beta₁ₑ、Beta₂ₑ,准确性为 0.6966292134831462,迭代次数为 173 次。
(三)贝叶斯逻辑回归
得到新的参数 Beta₀ₑ、Beta₁ₑ、Beta₂ₑ,准确性为 0.7356010452689,迭代次数为 693 次;以及新的参数 Beta₀ₑ、Beta₁ₑ、Beta₂ₑ,准确性为 0.7963,迭代次数为 1000 次。
六、模型评价
(一)优点
简单高效,适用于处理二元分类问题。
可解释性强,模型参数具有明确的实际意义。
对特征依赖性较小,在特征较少的情况下仍能进行有效预测。
(二)缺点
容易受到异常值影响,可能导致参数估计偏差较大。
无法处理复杂的非线性关系。
容易出现过拟合,尤其是在数据量较小或特征较多时。
七、结论
本文深入研究了逻辑回归模型在心脏病预测中的应用。通过对 UCI 心脏病数据集的分析,阐述了逻辑回归的原理、实现方法、优化策略和评价指标。尽管该模型存在一些不足,但在二元分类问题上仍具有一定优势。未来可进一步探索更有效的优化方法,提高模型的性能和泛化能力。
非参数化的自助重采样方法在Logistic回归应用及模型差异分析|附数据代码
本文探讨了计算逻辑回归参数抽样分布的不同方法,包括非参数化的自助重采样方法、参数化的自助方法以及一种混合模式。通过对这些方法的实施和分析,揭示了它们基于不同的建模假设,产生不同的结果。同时指出,在实际应用中,应根据差异的重要性选择最适合的方法,而不是认为某种方法是唯一正确的。
关键词:重采样;逻辑回归;参数化自助法;非参数化自助法
一、引言
计算抽样分布的不同方法会产生不同结果,但在实践中差异通常较小,我们可以选择方便的方法。本文由 Reddit 上的一个问题引发,探讨了逻辑回归的参数化引导问题中随机误差项的确定,并介绍了两种计算逻辑回归参数抽样分布的方法。本文将实施这些方法并解释其假设,提出混合方法,并给出选择方法的标准。
二、数据来源与处理
(一)数据来源
本文使用来自一般社会调查(GSS)的数据,存储库下载包含已重新采样的 GSS 数据子集的 HDF 文件。
(二)数据处理
导入所需的库,设置随机种子,下载数据文件并读取数据。
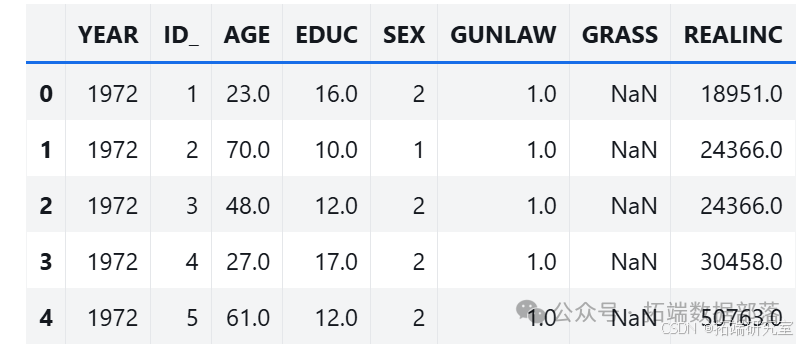
选取特定问题的数据,并对因变量进行重新编码。使用 GSS 中的一个关于大麻合法化的问题数据,将因变量中表示 “不应该合法化” 的值
2替换为0。
gss\['GRASS'\].value_counts()gss\['GRASS'\].replace(2, 0, inplace=True)为了对二次关系进行建模,添加包含
AGE和EDUC平方值的列,并删除有缺失值的行。
gss\['AGE2'\] = gss\['AGE'\]\*\*2gss\['EDUC2'\] = gss\['EDUC'\]\*\*2data = gss.dropna(subset=\['AGE', 'EDUC', 'SEX', 'GUNLAW', 'GRASS'\])三、逻辑回归结果
使用 StatsModels 进行逻辑回归,得到回归结果。绘制男性和女性受访者支持大麻合法化的预测概率随年龄变化的曲线。
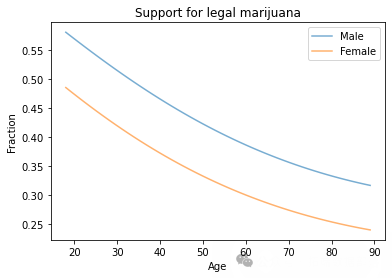
import statsmodels.formula.api as smfformula = 'GRASS ~ AGE + AGE2 + EDUC + EDUC2 + C(SEX)'result\_hat = smf.logit(formula, data=data).fit()result\_hat.summary()df = pd.DataFrame()df\['AGE'\] = np.linspace(18, 89)df\['EDUC'\] = 16df\['AGE2'\] = df\['AGE'\]\*\*2df\['EDUC2'\] = df\['EDUC'\]\*\*2df\['SEX'\] = 1pred1 = result\_hat.predict(df)pred1.index = df\['AGE'\]df\['SEX'\] = 2pred2 = result\_hat.predict(df)pred2.index = df\['AGE'\]pred1.plot(label='Male', alpha=0.6)pred2.plot(label='Female', alpha=0.6)plt.xlabel('Age')plt.ylabel('Fraction')plt.title('Support for legal marijuana')plt.legend();结果显示男性比女性更有可能支持合法化,年轻人比老年人更有可能支持合法化。
点击标题查阅往期内容

高维数据惩罚回归方法:主成分回归PCR、岭回归、lasso、弹性网络elastic net分析基因数据

左右滑动查看更多

01
02
03
04
四、非参数化自助重采样方法
(一)方法描述
基于自助重采样,对data的行进行有放回抽样,并对重新采样的数据运行回归模型。
options = dict(disp=False, start\_params=result\_hat.params)def bootstrap(i):bootstrapped = data.sample(n=len(data), replace=True)results = smf.logit(formula, data=bootstrapped).fit(**options)return results.params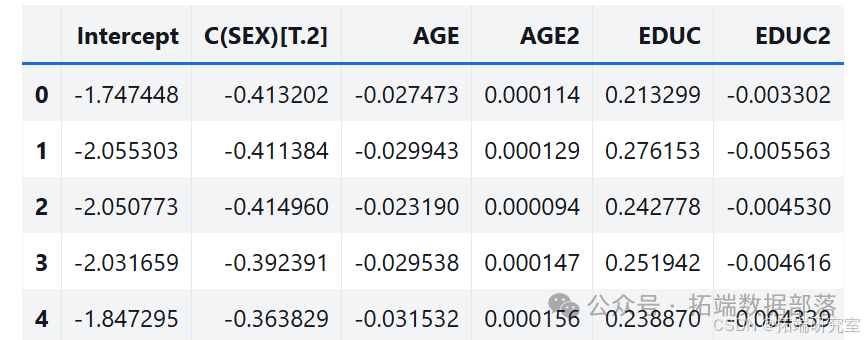
(二)结果分析
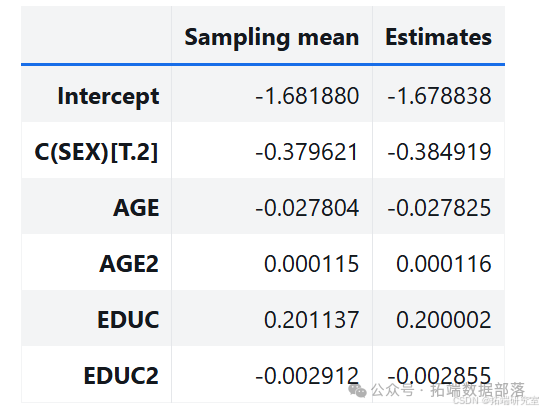
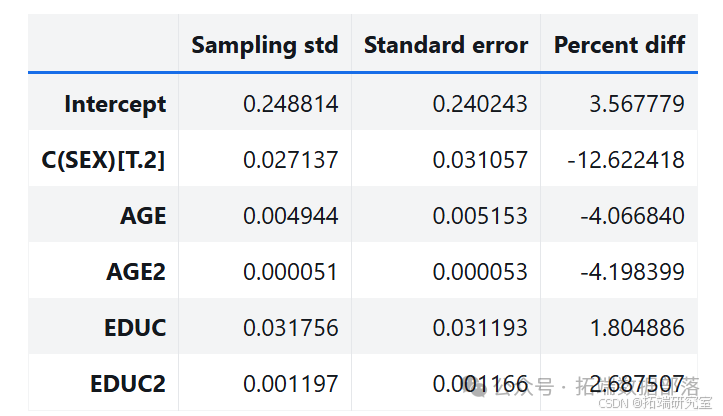
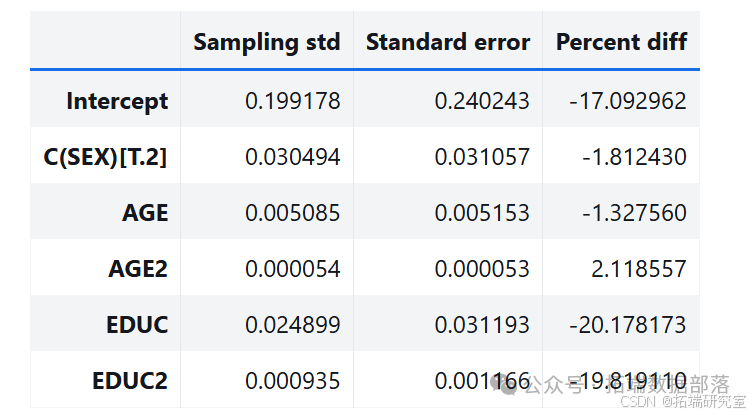
通过多次运行该过程,从抽样分布中生成样本。分析其中一个参数的抽样分布,发现抽样分布的平均值接近使用原始数据集估计的参数,标准差接近 StatsModels 计算的标准误差。
estimates = pqdm(range(101), bootstrap, n\_jobs=4)sampling\_dist = pd.DataFrame(estimates)ci90 = sampling\_dist\['C(SEX)\[T.2\]'\].quantile(\[0.05, 0.95\])sns.kdeplot(sampling\_dist\['C(SEX)\[T.2\]'\])\[plt.axvline(x, ls=':') for x in ci90\]plt.title('Sampling distribution of a parameter');pd.DataFrame({"Sampling mean": sampling\_dist.mean(),"Estimates": result\_hat.params})def standard\_errors(sampling\_dist, result\_hat):df = pd.DataFrame({"Sampling std": sampling\_dist.std(),"Standard error": result\_hat.bse})num, den = df.values.Tdf\['Percent diff'\] = (num / den - 1) * 100return dfstandard\_errors(sampling\_dist, result\_hat)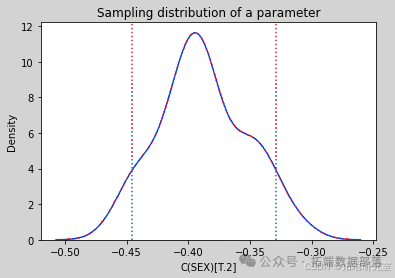
五、参数化自助方法
(一)方法描述
假设从原始数据中估计的参数是正确的,使用回归模型计算每个受访者的预测概率,然后用这些概率为每个受访者生成有偏差的抛硬币,将模拟值作为因变量运行回归模型。
pi\_hat = result\_hat.predict(data)from scipy.stats import bernoullisimulated = bernoulli.rvs(pi\_hat.values)def bootstrap2(i):flipped = data.assign(GRASS=bernoulli.rvs(pi\_hat.values))results = smf.logit(formula, data=flipped).fit(**options)return results.params(二)结果分析
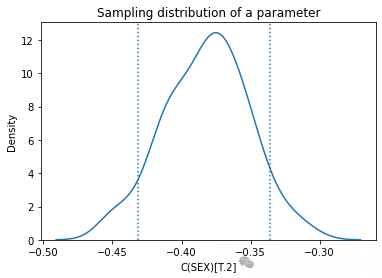
多次运行该方法得到抽样分布样本,分析参数的抽样分布,其标准差也接近标准误差。
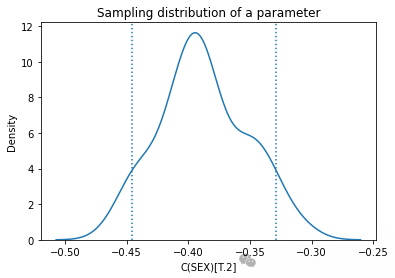
estimates = pqdm(range(101), bootstrap2, n\_jobs=4)sampling\_dist2 = pd.DataFrame(estimates)ci90 = sampling\_dist2\['C(SEX)\[T.2\]'\].quantile(\[0.05, 0.95\])sns.kdeplot(sampling\_dist2\['C(SEX)\[T.2\]'\])\[plt.axvline(x, ls=':') for x in ci90\]plt.title('Sampling distribution of a parameter');standard\_errors(sampling\_dist2, result_hat)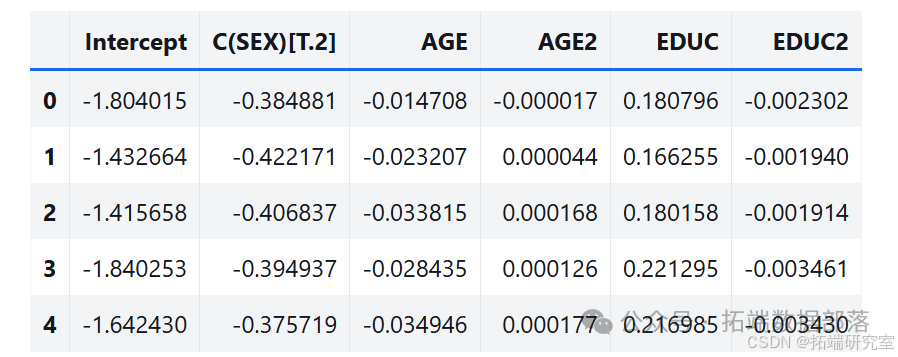
六、混合模式方法
(一)方法描述
结合非参数化和参数化方法,先使用自助抽样模拟调查不同的人,再用参数化方法模拟他们的响应。
def bootstrap3(i):bootstrapped = data.sample(n=len(data), replace=True)pi\_hat = result\_hat.predict(bootstrapped)flipped = bootstrapped.assign(GRASS=bernoulli.rvs(pi_hat.values))results = smf.logit(formula, data=flipped).fit(**options)return results.params(二)结果分析
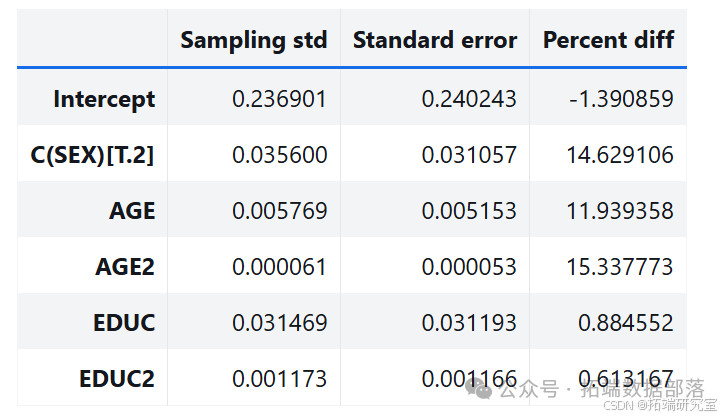
得到抽样分布样本,分析参数的抽样分布,标准误差与 StatsModels 计算的误差相当。
estimates = pqdm(range(101), bootstrap3, n\_jobs=4)sampling\_dist3 = pd.DataFrame(estimates)ci90 = sampling\_dist3\['C(SEX)\[T.2\]'\].quantile(\[0.05, 0.95\])sns.kdeplot(sampling\_dist3\['C(SEX)\[T.2\]'\])\[plt.axvline(x, ls=':') for x in ci90\]plt.title('Sampling distribution of a parameter');standard\_errors(sampling\_dist3, result_hat)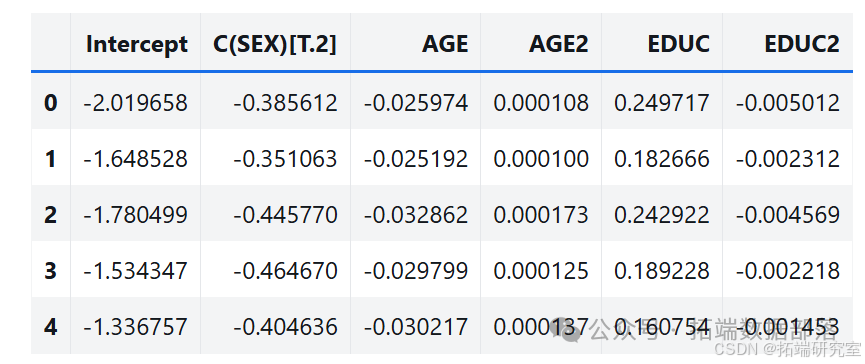
七、讨论与结论
(一)不同方法的比较
本文介绍了三种计算抽样分布的方法,它们基于不同的抽样过程模型,产生不同的结果。在某些情况下,不同方法可能渐近收敛于相同结果,但对于有限数据集通常不同。
(二)选择方法的标准
如果差异较小,在实践中可能无关紧要,可以选择最容易实现、计算最快或方便的方法。不能认为分析方法的结果是唯一正确的,它们也基于建模假设和近似值。
综上所述,在实际应用中应根据具体情况选择合适的方法来计算逻辑回归参数的抽样分布。
关于分析师

在此对 Anting Li 对本文所作的贡献表示诚挚感谢,她在中央财经大学完成了应用统计学专业的硕士学位,专注统计学领域。擅长 R 语言、Python、Matlab。

本文中分析的数据、代码分享到会员群,扫描下面二维码即可加群!
资料获取
在公众号后台回复“领资料”,可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现》。
点击标题查阅往期内容
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
PYTHON银行机器学习:回归、随机森林、KNN近邻、决策树、高斯朴素贝叶斯、支持向量机SVM分析营销活动数据|数据分享
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
MATLAB随机森林优化贝叶斯预测分析汽车燃油经济性
R语言中贝叶斯网络(BN)、动态贝叶斯网络、线性模型分析错颌畸形数据
使用贝叶斯层次模型进行空间数据分析
MCMC的rstan贝叶斯回归模型和标准线性回归模型比较
python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
Python贝叶斯推断Metropolis-Hastings(M-H)MCMC采样算法的实现
matlab贝叶斯隐马尔可夫hmm模型实现
贝叶斯线性回归和多元线性回归构建工资预测模型
Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据
R语言STAN贝叶斯线性回归模型分析气候变化影响北半球海冰范围和可视化检查模型收敛性
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据
R语言JAGS贝叶斯回归模型分析博士生延期毕业完成论文时间
R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
Python决策树、随机森林、朴素贝叶斯、KNN(K-最近邻居)分类分析银行拉新活动挖掘潜在贷款客户
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
随机森林优化贝叶斯预测分析汽车燃油经济性
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
Python贝叶斯回归分析住房负担能力数据集
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
Python用PyMC3实现贝叶斯线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言Gibbs抽样的贝叶斯简单线性回归仿真分析
R语言和STAN,JAGS:用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言贝叶斯线性回归和多元线性回归构建工资预测模型
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言stan进行基于贝叶斯推断的回归模型
R语言中RStan贝叶斯层次模型分析示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
视频:R语言中的Stan概率编程MCMC采样的贝叶斯模型
R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计



![]()





![[数据集][目标检测]手机识别检测数据集VOC+YOLO格式9997张1类别](https://i-blog.csdnimg.cn/direct/64685cdaf4b34c31838a52310e11cb9f.png)