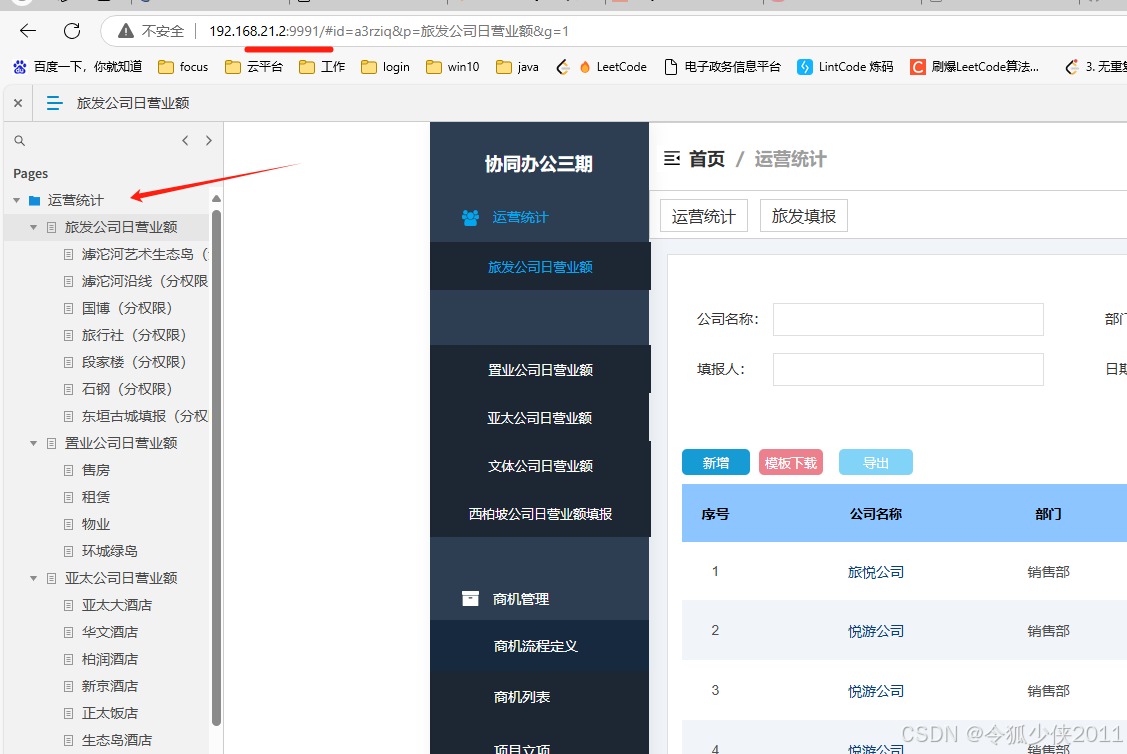
一、 衍射现象
波遇到障碍物时,绕过障碍物 进入几何阴影区。
光偏离直线传播路径进入几何 阴影区,并形成光强非均匀稳 定分布。
二、菲涅耳原理
1、 惠更斯原理
波面上的每一点均为发 射子波的波源,这些子波的 包络面即新的波阵面
成功:可解释衍射成因,用几何法作出新的波面, 推导反射、折射定律
不足:不能定量说明衍射波的强度分布
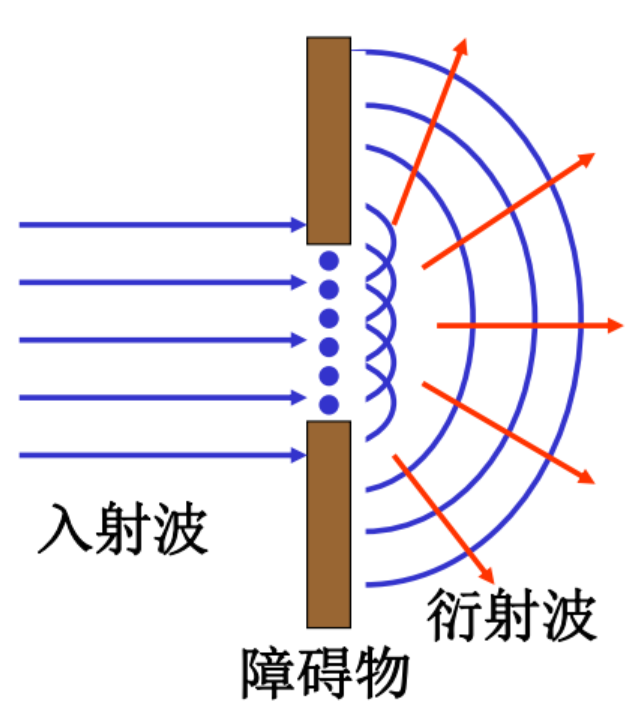
2、 菲涅耳原理
1、对子波的振幅和相位作了定量描述
波面上各面元 —— 子波源
2、空间任一点振动为所有子波在该点相干叠加的结果
有限个分立相干波叠加 —— 干涉
无限多个连续分布子波源相干叠加 —— 衍射
3、衍射分类
菲涅耳衍射(近场衍射):

夫琅和费衍射(远场衍射)

即平行光衍射
信息光学(现代光学分支)
三. 单缝夫琅和费衍射
1、 装置:
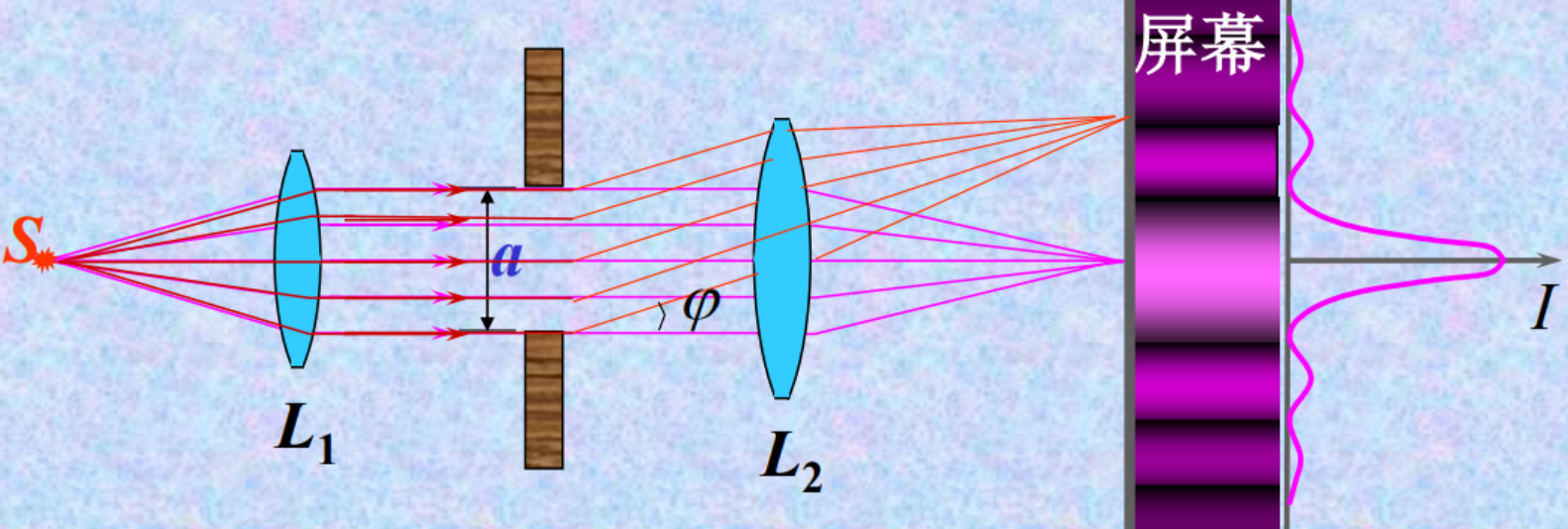
缝宽a: 其上每一点均为子波源,发出衍射光
衍射角φ:衍射光线与波面法线夹角
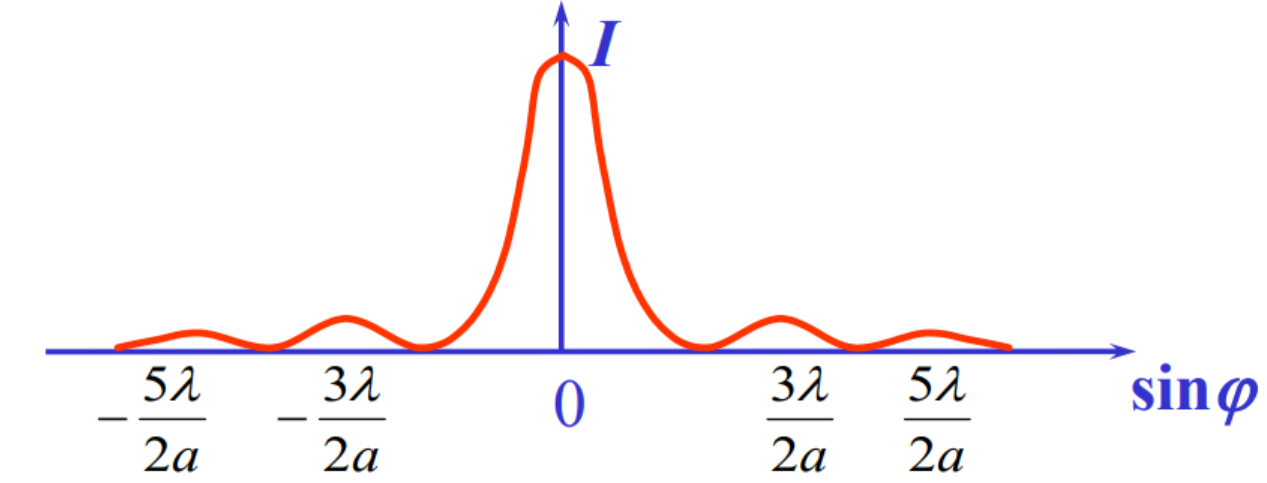
当φ=0,衍射光线汇集于L2 焦点F,Δ=0 中央明纹中心
当φ≠0,衍射光线汇集于L2 焦平面上某点P,Δ≠0,P处光强可由菲涅耳公式计算
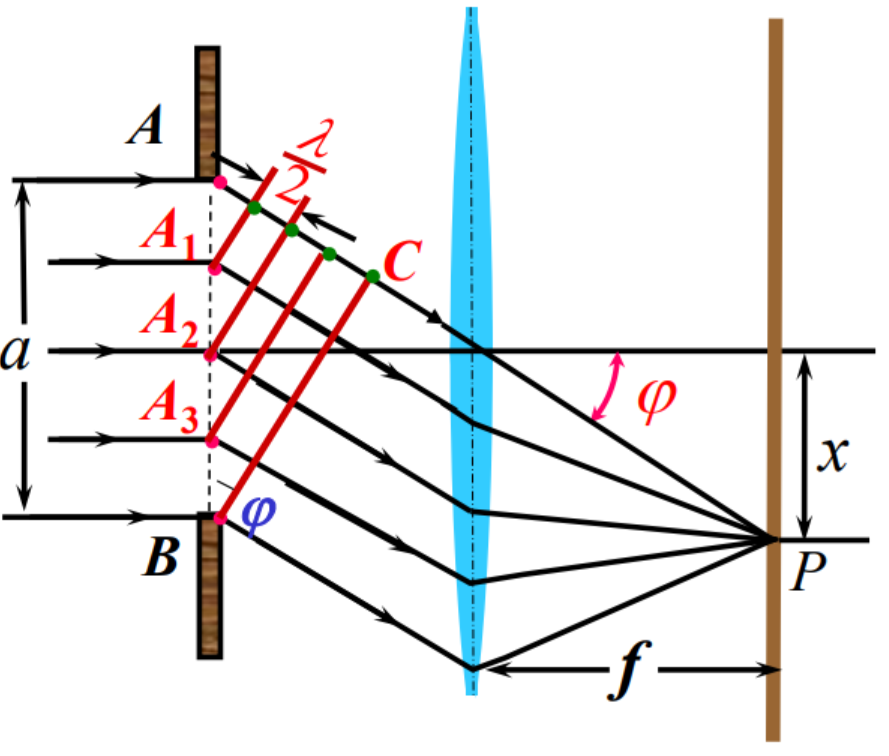
2、 菲涅耳半波带法(半定量方法)
衍射角为φ的一束平行光线的最大光程差: Δ m a x = ∣ A C ∣ = a s i n ϕ \Delta_{max}=|AC|=asin\phi Δmax=∣AC∣=asinϕ
用 λ 2 \frac{\lambda}2 2λ去分 Δ m a x \Delta_{max} Δmax,假设 Δ m a x = n λ 2 \Delta_{max}=n\frac{\lambda}2 Δmax=n2λ
对应的单缝a被分为 n个半波带
相邻的半波带中的对应光线在缝外引起的光程差为 λ 2 \frac{\lambda}2 2λ
n =0 φ=0 对应中央明纹中心
相邻两半波带中对应光线 Δ = λ 2 , Δ ϕ = π \Delta=\frac{\lambda}2,\Delta\phi=\pi Δ=2λ,Δϕ=π,两两相消, 屏上相聚点为暗纹
n为偶数: 刚好两两相消
n为奇数: 剩下一个半波带中的衍射光线未被抵消 对应的屏上相聚点为明纹中心
n 不是整数:对应非明、暗纹中心的其余位置
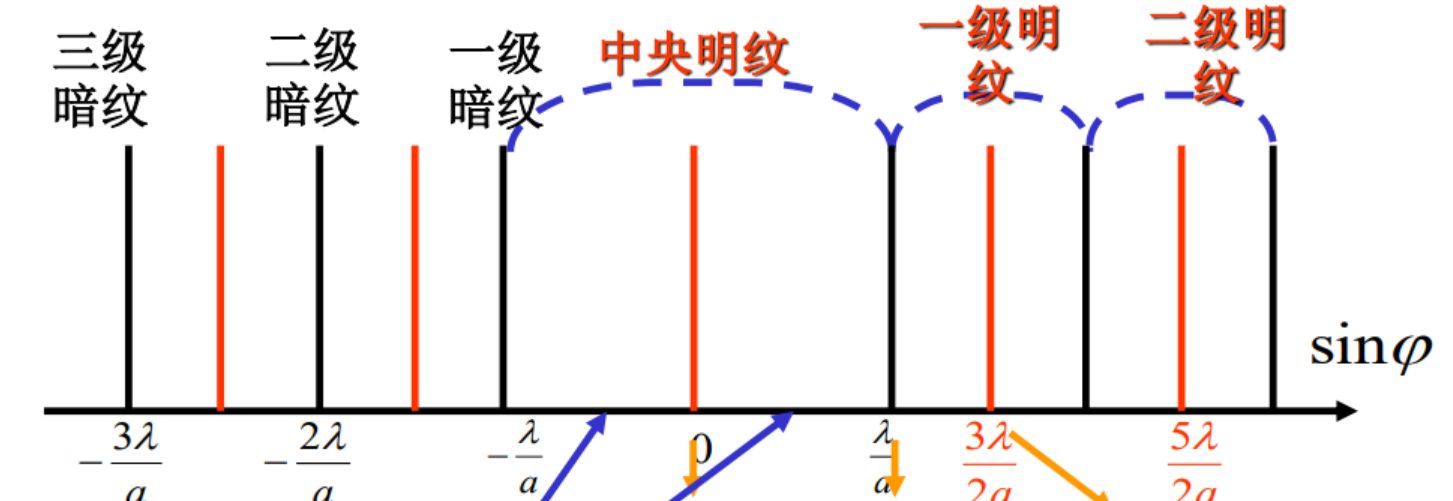
明暗纹条件:
KaTeX parse error: Unknown column alignment: * at position 63: … \begin{array}{*̲*lr**} …
双缝干涉中明暗纹条件为:
KaTeX parse error: Unknown column alignment: * at position 58: … \begin{array}{*̲*lr**} …
二者明暗纹条件不同是因为计算光程差的方式不同,干涉是两个缝的光程差,衍射是划分成数个半波带,半波带之间的光程差。
单缝衍射明暗纹条件中k值不能取零,因为k=0对应中央明纹区。
计算衍射条纹角宽度
计算角宽度,可以通过计算两个条纹之间的距离:
KaTeX parse error: Unknown column alignment: * at position 60: … \begin{array}{*̲*lr**} …
中央明纹宽度
2
λ
a
\frac{2\lambda}{a}
a2λ
其余明纹 λ a \frac{\lambda}{a} aλ
计算衍射条纹线宽度
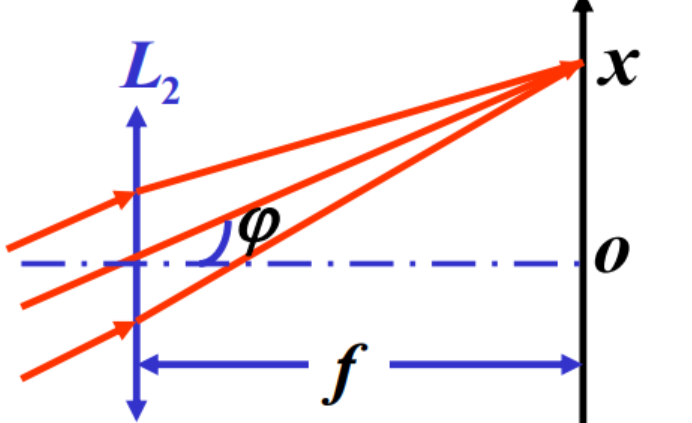
x = f t a n ϕ x=ftan\phi x=ftanϕ
Δ x = f ( t a n ϕ 2 − t a n ϕ 1 ) ≈ f ( ϕ 2 − ϕ 1 ) = f Δ ϕ \Delta x=f(tan\phi_2-tan\phi_1)\approx f(\phi_2-\phi_1)=f\Delta \phi Δx=f(tanϕ2−tanϕ1)≈f(ϕ2−ϕ1)=fΔϕ
中央明纹 2 λ a f \frac{2\lambda}{a}f a2λf
其余明纹 λ a f \frac{\lambda}{a}f aλf
条纹亮度分布
由菲涅尔波带法:
- 中央明纹中心: 全部光线干涉相长
- 一级明纹中心: 1 3 \frac13 31部分光线干涉相长
- 二级明纹中心: 1 5 \frac15 51部分光线干涉相长
四、圆孔衍射 光学仪器的分辨率
1、装置:
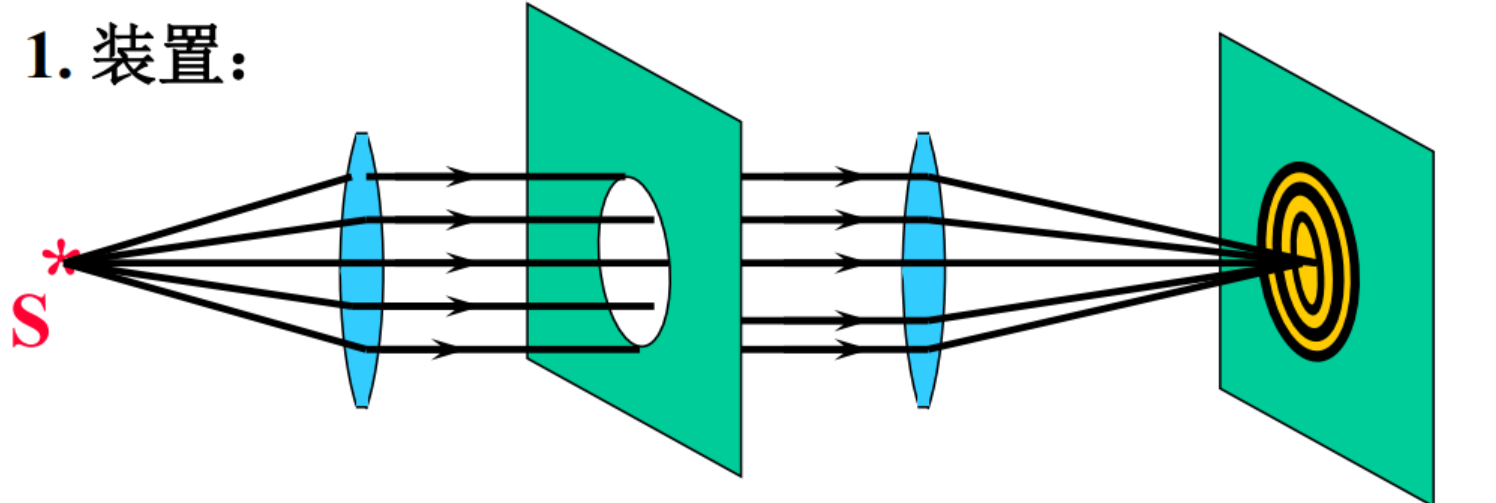
2.条纹:
明暗相间同心圆环
中央亮纹:爱里斑
- 集中大部分能量
- 角宽度为其余明纹2倍
- 半角宽度: 1.22 λ D 1.22\frac{\lambda}D 1.22Dλ
3、 光学仪器分辨率
物镜 ~ 圆孔
物点的象 ~ 衍射图样
瑞利准则:第一个象的爱里斑边沿与第二个象的爱里斑中心重合 —— 恰能分辨
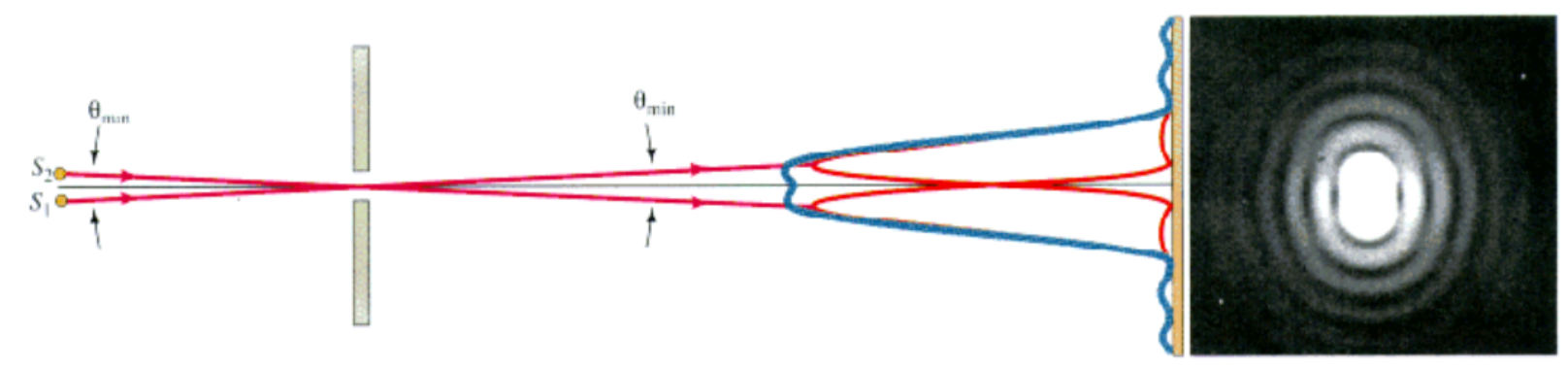
最小分辨角: Δ ϕ = 1.22 λ D \Delta \phi=1.22\frac{\lambda}{D} Δϕ=1.22Dλ
光学仪器分辨率
1 Δ ϕ = D 1.22 λ \frac1{\Delta \phi}=\frac{D}{1.22\lambda} Δϕ1=1.22λD
提高分辨率途径 D↑,λ↓
五、光栅夫琅和费衍射
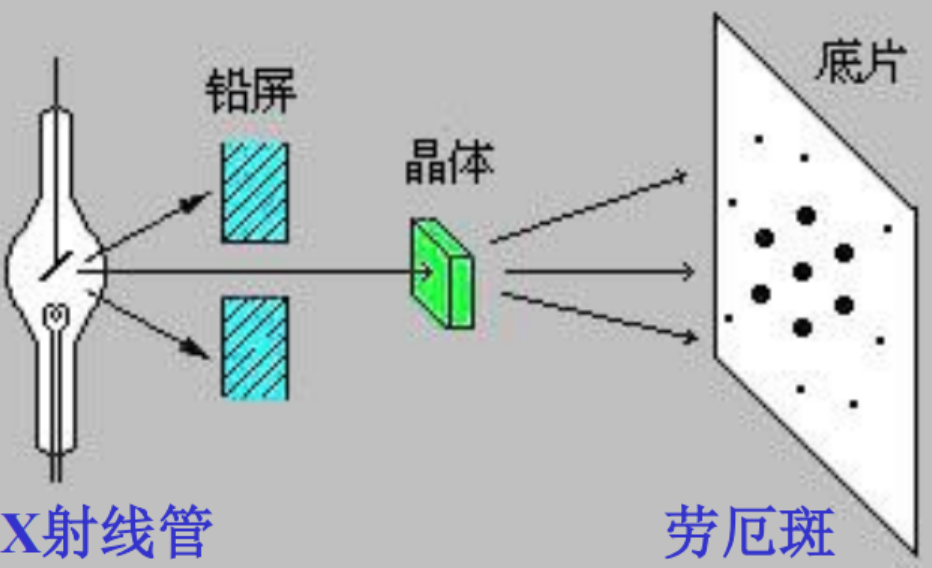
六、晶格衍射(X光衍射)
X射线:1895年,德国,伦琴在阴极射线实验中发现。 特点:不带电,穿透本领强。为研究其波动 性,寻找相应的光栅(晶体点阵)
布拉格公式:
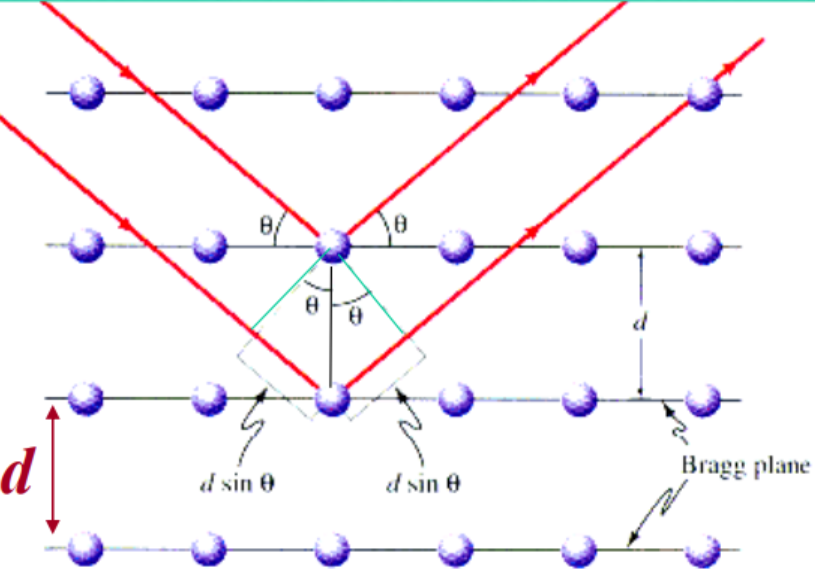
2 d s i n θ = k λ 2dsin\theta=k\lambda 2dsinθ=kλ
应用:研究晶体结构,测晶格常数



![[数据库实验七]事务设计](https://i-blog.csdnimg.cn/direct/687e9b3965104b36a1d7d735528a8d5f.png)