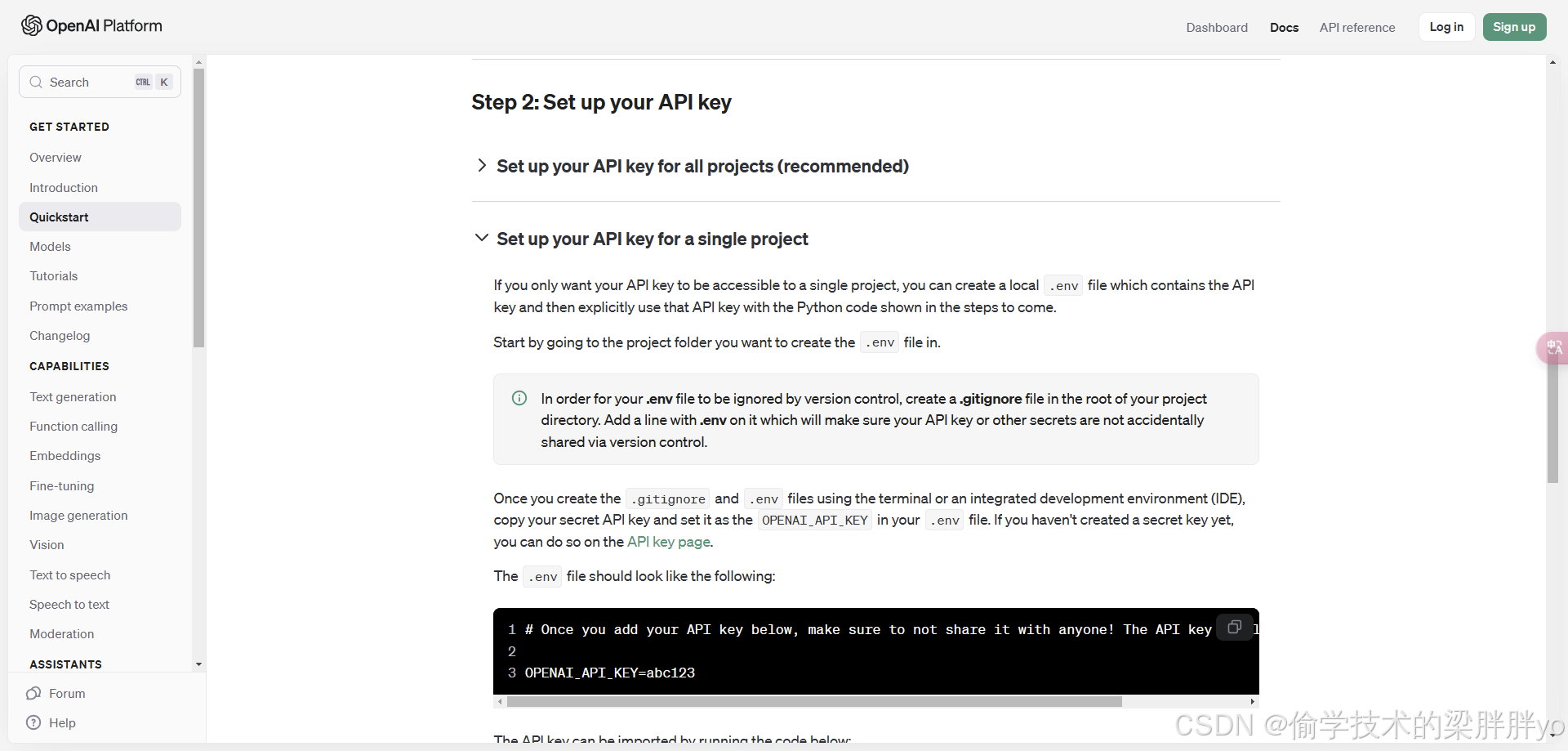
需求：当双击表格某一行任意位置时，自动勾选上其前面的复选框

1、在el-table 组件的每一行添加@row-dblclick事件，用于双击点击

  <el-table
        :data="tableData"
        ref="tableRef"
 @selection-change="handleSelectionChange"
        @row-dblclick="handleRowClick"
      >
<el-table-column type="selection" fixed width="55" align="center" />
        <el-table-column
          type="index"
          fixed
          label="序号"
          width="75"
          align="center"
        />
</el-table>

2、定义方法在 `handleRowClick` 方法中，通过修改 `row` 对象中的某个属性来标记该行是否被选中，调用 `toggleRowSelection` 方法来切换多选框的勾选状态。

const sourceRef = ref();

//双击
const handleRowClick = (row) => {
  console.log(row, "双击--");
  row.isSelected = !row.isSelected;
  tableRef.value.toggleRowSelection(row);
};