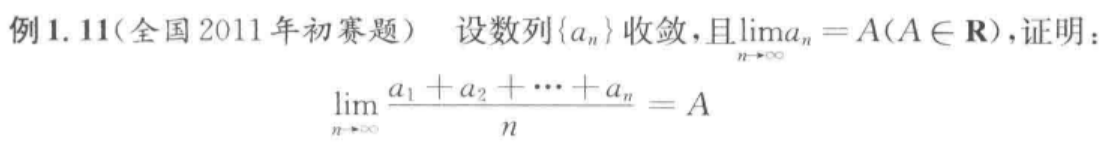
已知:
∀
ε
>
0
,
∃
n
>
N
,
∣
a
n
−
A
∣
<
ε
\forall \varepsilon >0, \exist n>N,|a_n-A|<\varepsilon
∀ε>0,∃n>N,∣an−A∣<ε
目标:
∀
ε
>
0
,
∃
n
>
N
1
,
∣
a
1
+
.
.
.
+
a
n
n
−
A
∣
<
ε
\forall \varepsilon >0, \exist n>N_1,|\frac{a_1+...+a_n}{n}-A|<\varepsilon
∀ε>0,∃n>N1,∣na1+...+an−A∣<ε
假设
S
n
=
a
1
+
.
.
.
+
a
n
S_n=a_1+...+a_n
Sn=a1+...+an,则变成了求
∣
S
n
n
−
A
∣
<
ε
|\frac{S_n}n-A|<\varepsilon
∣nSn−A∣<ε
由已知条件,
n
>
N
,
∣
a
n
−
A
∣
<
ε
n>N,|a_n-A|<\varepsilon
n>N,∣an−A∣<ε,把n个数分为小于等于N的和大于N的分别处理,
∣
S
n
n
−
A
∣
<
∣
S
N
+
N
∣
A
∣
+
∣
a
N
+
1
−
A
∣
+
.
.
.
+
∣
a
n
−
A
∣
n
∣
<
∣
S
N
+
N
∣
A
∣
+
(
n
−
N
)
ε
n
∣
<
∣
S
N
+
N
∣
A
∣
+
ε
n
∣
|\frac{S_n}n-A|<|\frac{S_N+N|A|+|a_{N+1}-A|+...+|a_n-A|}n|<|\frac{S_N+N|A|+(n-N)\varepsilon}n|<|\frac{S_N+N|A|+\varepsilon}n|
∣nSn−A∣<∣nSN+N∣A∣+∣aN+1−A∣+...+∣an−A∣∣<∣nSN+N∣A∣+(n−N)ε∣<∣nSN+N∣A∣+ε∣
因为 S N , N ∣ A ∣ S_N,N|A| SN,N∣A∣是常数,所以 l i m n − > ∞ S N + N ∣ A ∣ n = 0 lim_{n->\infin}\frac{S_N+N|A|}n=0 limn−>∞nSN+N∣A∣=0,所以当 N 1 > N N_1>N N1>N时 l i m n − > ∞ ∣ S n n − A ∣ < ε lim_{n->\infin}|\frac{S_n}n-A|<\varepsilon limn−>∞∣nSn−A∣<ε