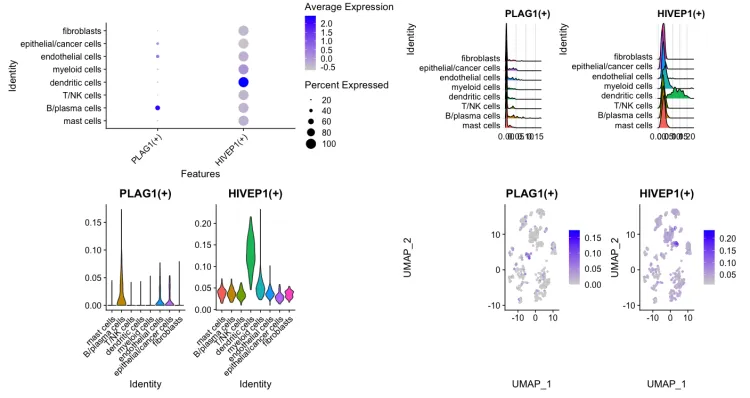
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:将矩阵按对角线排序
出处:1329. 将矩阵按对角线排序
难度
5 级
题目描述
要求
矩阵对角线是一条从矩阵最上面行或者最左侧列中的某个元素开始的对角线,沿右下方向一直到矩阵末尾的元素。例如,矩阵 mat \texttt{mat} mat 有 6 \texttt{6} 6 行 3 \texttt{3} 3 列,从 mat[2][0] \texttt{mat[2][0]} mat[2][0] 开始的矩阵对角线将会经过 mat[2][0] \texttt{mat[2][0]} mat[2][0]、 mat[3][1] \texttt{mat[3][1]} mat[3][1] 和 mat[4][2] \texttt{mat[4][2]} mat[4][2]。
给定一个 m × n \texttt{m} \times \texttt{n} m×n 的整数矩阵 mat \texttt{mat} mat,将每条矩阵对角线上的元素按升序排序,返回排序后的矩阵。
示例
示例 1:

输入:
mat
=
[[3,3,1,1],[2,2,1,2],[1,1,1,2]]
\texttt{mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]}
mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出:
[[1,1,1,1],[1,2,2,2],[1,2,3,3]]
\texttt{[[1,1,1,1],[1,2,2,2],[1,2,3,3]]}
[[1,1,1,1],[1,2,2,2],[1,2,3,3]]
示例 2:
输入:
mat
=
[[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
\texttt{mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]}
mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
输出:
[[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
\texttt{[[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]}
[[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
数据范围
- m = mat.length \texttt{m} = \texttt{mat.length} m=mat.length
- n = mat[i].length \texttt{n} = \texttt{mat[i].length} n=mat[i].length
- 1 ≤ m, n ≤ 100 \texttt{1} \le \texttt{m, n} \le \texttt{100} 1≤m, n≤100
- 1 ≤ mat[i][j] ≤ 100 \texttt{1} \le \texttt{mat[i][j]} \le \texttt{100} 1≤mat[i][j]≤100
前言
这道题要求对给定矩阵的每条矩阵对角线上的元素按升序排序,因此必须对每条矩阵对角线分别排序。
在 m × n m \times n m×n 的矩阵中有 m + n − 1 m + n - 1 m+n−1 条矩阵对角线,最长的矩阵对角线的长度是 min ( m , n ) \min(m, n) min(m,n)。在确定 m m m 和 n n n 的情况下,时间复杂度取决于每条矩阵对角线的排序的时间复杂度。由于这道题中 m m m 和 n n n 都不超过 100 100 100,因此可以使用时间复杂度较高的初级排序算法,空间复杂度是 O ( 1 ) O(1) O(1)。
此处只给出基于插入排序的矩阵对角线排序,读者可以自行尝试实现基于其他初级排序算法、高级排序算法以及线性时间排序算法的矩阵对角线排序。
解法
思路和算法
在 m × n m \times n m×n 的矩阵中有 m + n − 1 m + n - 1 m+n−1 条矩阵对角线,每条矩阵对角线的起始单元格可能有以下两种情况:
-
当起始单元格的列下标为 0 0 0 时,起始单元格位于最左侧列;
-
当起始单元格的行下标为 0 0 0 且列下标大于 0 0 0 时,起始单元格位于最上面行。
为了避免同一条矩阵对角线被重复计算,当起始单元格的行下标为 0 0 0 时不考虑列下标为 0 0 0 的情况。
用 ( startRow , startCol ) (\textit{startRow}, \textit{startCol}) (startRow,startCol) 表示矩阵对角线的起始单元格,则矩阵对角线的长度是 min ( m − startRow , n − startCol ) \min(m - \textit{startRow}, n - \textit{startCol}) min(m−startRow,n−startCol),矩阵对角线中的第 i i i 个元素( i i i 从 0 0 0 开始)位于单元格 ( startRow + i , startCol + i ) (\textit{startRow} + i, \textit{startCol} + i) (startRow+i,startCol+i)。
对每条矩阵对角线使用插入排序,当每条矩阵对角线的排序结束之后,整个矩阵排序结束。
代码
class Solution {
int m, n;
public int[][] diagonalSort(int[][] mat) {
m = mat.length;
n = mat[0].length;
for (int i = 0; i < m; i++) {
diagonalSort(mat, i, 0);
}
for (int j = 1; j < n; j++) {
diagonalSort(mat, 0, j);
}
return mat;
}
public void diagonalSort(int[][] mat, int startRow, int startCol) {
int length = Math.min(m - startRow, n - startCol);
for (int i = 1; i < length; i++) {
int num = mat[startRow + i][startCol + i];
int insertIndex = i;
for (int j = i - 1; j >= 0 && mat[startRow + j][startCol + j] > num; j--) {
mat[startRow + j + 1][startCol + j + 1] = mat[startRow + j][startCol + j];
insertIndex = j;
}
if (insertIndex != i) {
mat[startRow + insertIndex][startCol + insertIndex] = num;
}
}
}
}
复杂度分析
-
时间复杂度: O ( ( m + n ) × min ( m , n ) 2 ) O((m + n) \times \min(m, n)^2) O((m+n)×min(m,n)2),其中 m m m 和 n n n 分别是矩阵 mat \textit{mat} mat 的行数和列数。共有 m + n − 1 m + n - 1 m+n−1 条矩阵对角线,每条矩阵对角线的插入排序需要 O ( min ( m , n ) 2 ) O(\min(m, n)^2) O(min(m,n)2) 的时间,时间复杂度是 O ( ( m + n ) × min ( m , n ) 2 ) O((m + n) \times \min(m, n)^2) O((m+n)×min(m,n)2)。
-
空间复杂度: O ( 1 ) O(1) O(1)。