[导读]：超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成，后续会不定期解读蓝桥杯真题，这是Scratch蓝桥杯真题解析第191讲。

如果想持续关注Scratch蓝桥真题解读，可以点击《Scratch蓝桥杯历年真题》并订阅合集，查阅教程更方便。

第15届蓝桥杯省赛已于2024年8月24日落下帷幕，中级组编程题一共有6题，分别如下：

• 抓不住的蜜蜂

• 穿越病毒区

• 画台扇

• 收集松果

• 占领矩阵

• 截取递增数

截取递增数，本题是2024年8月24日举行的第15届蓝桥省赛Scratch中级组编程第6题，题目要求编程截取递增数。要求对一个不含0的九位数，获取所有的递增数并存入列表，如果没有就说“NO”，按下空格键对列表中的递增数排序，然后说出最大的数字。

先来看看题目的要求吧。

一.题目说明

背景信息：

递增数：如果一个大于9的正整数各个数位上的数，从左到右是逐渐变大的，那么就称这个数为递增数。

例如：124、248 是递增数。

给你一个不含 0的九位数，请找出从这个九位数中能截取出的所有递增数。

例如：115367482能够截取出的递增数有：15、36、 67、367、48。

注意：只能截取若干个连续的数。

编程实现：

截取递增数

具体要求：

1). 点击绿旗，列表1为空，熊猫说“请输入一个不含0的九位数”，同时舞台下方显示示榆入框，如图所示；

例如：输入115367482

2). 如果输入的整数不能截取出递增数，熊猫说“NO”，1秒后程序结束；

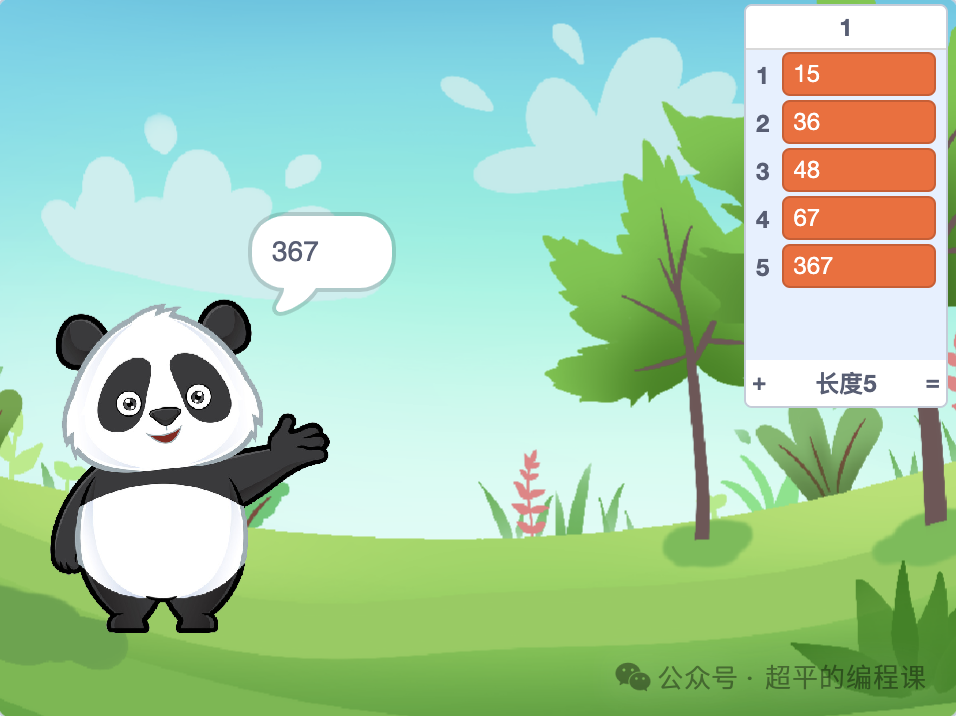
3). 如果输入的整数能截取出递增数，那么在列表 1中呈现出截取的所有递增数，如图所示；

4). 得到所有递增数之后，按下空格按键，列表1中的数按照从小到大的顺序重新排列，如图所示；

5). 最后，熊猫说出列表1中的最大数，如图所示，1秒后程序结束。

评判标准：

• 5 分：满足"具体要求"中的1）；

• 28分：满足"具体要求"中的2）；

• 28分：满足"具体要求"中的3）；

• 25 分：满足"具体要求"中的4）；

• 14分：满足"具体要求"中的5）。

二.思路分析

本题只有一个角色，就是熊猫，如图所示：

这是一道算法题，考查的知识点主要包括字符串处理、列表运算、嵌套循环和排序算法等。

对于本题而言，有两个关键点：

• 获取递增数

• 列表排序

关于列表排序，在历届真题中出现过多次，最近一次是2024年1月28日，具体的分析讲解可以参考《选择排序-第15届蓝桥第4次STEMA测评Scratch真题精选》这篇教程，这里就不再赘述了。

我们的重点是如何获取递增数？

首先要理解递增数的概念，就像生活中的排队现象，按照从小到大的顺序依次排列，如图：

如果一个小朋友代表一位数字的话，整体就构成一个递增数，比如下图中的1234：

我们以题目给出的数字115367482进行分析，在这个9位数中，有如下5个递增数：

15, 36, 367, 67, 48

仔细分析这些递增数，你发现了什么？

简单来说，有如下两个特点：

1). 递增数至少是两位数；

2). 递增数的一部分也是递增数；

尤其是第二点，非常重要，比如367是递增数，36和67是367的一部分，它们也是递增数。

因此，我们可以遍历整个九位数，把每一位数字当做起点，逐个往后比较，直到当前数字不大于后一位数字，同时将得到的递增数字存入到列表中。

为方便描述，我们使用变量"i"表示循环的轮数，变量“j”表示数字的起点。

第一轮循环，i = 1，将第1个数字1作为起点，进行循环处理，如下：

数字：115367482j = 1，第j个数字为1，第j+1个数字为11 < 1不成立，循环结束本轮循环没有递增数

第二轮循环，i = 2，将第2个数字1作为起点，循环判断，如下：​​​​​​​

数字：115367482j = 2，第j个数字为1，第j+1个数字为51 < 5成立，j增加1，找到一个递增数15j = 3，第j个数字为5，第j+1个数字为35 < 3不成立，循环结束本轮循环找到一个递增数15

第三轮循环，i = 3，将第3个数字5作为起点，循环判断，如下：​​​​​​​

数字：115367482j = 3，第j个数字为5，第j+1个数字为35 < 3不成立，循环结束本轮循环没有递增数

第四轮循环，i = 4，将第4个数字3作为起点，循环判断，如下：​​​​​​​

数字：115367482j = 4，第j个数字为3，第j+1个数字为63 < 6成立，j增加1，找到一个递增数36j = 5，第j个数字为6，第j+1个数字为76 < 7成立，j增加1，找到一个递增数367j = 6，第j个数字为7，第j+1个数字为46 < 4不成立，循环结束本轮循环找到两个递增数36和367

第五轮循环，i = 5，将第5个数字3作为起点，循环判断，如下：​​​​​​​

数字：115367482j = 5，第j个数字为6，第j+1个数字为76 < 7成立，j增加1，找到一个递增数67j = 6，第j个数字为7，第j+1个数字为46 < 4不成立，循环结束本轮循环找到一个递增数67

以此类推，循环8轮（最后只有1个数字，无需判断），就可以找到所有的递增数了，这是一个嵌套循环的过程。

思路有了，接下来，我们就进入程序实现环节。

三.编程实现

根据上面的思路分析，我们分3步来完成作品：

• 获取递增数

• 列表排序

• 完成主程序

1. 获取递增数

根据前面的思路分析，我们定义一个自制积木用于获取递增数，代码如下：

代码挺多的，说明5点：

1). 要处理的数字直接使用“回答”指令获取；

2). 递增数至少需要两位，所以最后一位数字不用处理，循环的轮数等于“回答的字符数 - 1”；

3). 每一轮循环，要将变量“数字”设置为空字符串，只要当前数字小于后一位数字，就将其追加到“数字”的后面，内层循环结束时，还需要把第j个数字连接起来；

4). 以第i个字符作为起点时，对于一个长度大于2的递增数，它有多个递增数，比如367和36，因此在内层循环时，要将这些子递增数都加入到列表；

5). 由于递增数至少是两位，对于加入列表的数字需要进行判断，这就是“如果数字 > 9 那么”指令的作用；

2. 列表排序

我们使用选择排序算法对列表中的递增数进行排序，为了方便，也将其定义成一个自制积木，编写代码如下：

选择排序的核心思想是这样的，对于长度为n的列表，进行n轮排序，每一轮（用i表示）在未排序的数据中，找到最小的列表项，放到第i位，这需要使用嵌套循环来实现。

3. 完成主程序

接下来，在绿旗指令下编写代码如下：

代码比较简单，说明3点：

1). 列表一定要清空；

2). 如果没有递增数，在说完“NO”后，直接停止全部脚本；

3). 对于按键的处理，使用“等待条件”指令最简单，效果也最好；

至此，整个作品就创作好了，是时候来测试自己的作品啦。

四.总结与思考

本题是中级组编程部分第6题，分数为100分，积木块数量100个左右，涉及到的知识点主要包括：

• 字符串运算；

• 列表处理；

• 嵌套循环；

• 排序算法；

作为本次中级组省赛的第6题，也是压轴题，难度较大，完成时间25分钟左右。本题的难点有两个，一是如何获取递增数，二是列表排序。

其中，排序算法在历届真题中已经出现了多次，涉及排序的作品有10来个左右，这是我们必须掌握的基础算法。

真正有难度的是如何获取递增数，在Python和C++中，递增数是常客，但是在Scratch竞赛中，这是第一次出现。这说明Scratch竞赛逐渐开始算法化，对于基础不错的孩子，在平时的学习过程中，应该多关注一下算法层面的练习和思考。

获取递增数的实现并没有那么复杂，关键是要分析递增数的构成规律，确定好寻找递增数的方法，代码层面其实就是嵌套循环和字符串处理。

超平老师给你留一道思考题，如果需要判断输入的数字是否为不含0的九位数，你知道该怎么实现吗？

你还有什么好的方法吗，非常欢迎您和超平老师交流分享。

如果你觉得文章对你有帮助，别忘了点赞和转发，予人玫瑰，手有余香😄

需要素材和源码的，可以移步至“超平的编程课”gzh。