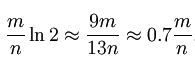目录
- 二叉树进阶
- 1.二叉搜索树
- 1.1二叉搜索树的实现
- 1.1.1二叉搜索树的查找
- 1.1.2二叉搜索树的插入
- 1.1.3中序遍历(排序)
- 1.1.4二叉搜索树的删除(重点)
- 1.2二叉搜索树的应用
- 1.2.1K模型
- 1.2.2KV模型
- 1.3二叉搜索树的性能分析
二叉树进阶
前言:
- map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
- 二叉搜索树的特性了解,有助于更好的理解map和set的特性
- 之所以不在之前讲,是因为有些模拟实现和oj题用c语言实现比较麻烦
1.二叉搜索树
二叉搜索树又称二叉排序树,它可能是一棵空树,或者是具有以下性质的二叉树:
- 若左子树不为空,则所有左子树的节点值一定比跟的值小
- 若右子树不为空,则所有右子树的节点值一定比根的值大
- 所有左右子树都是二叉搜索树
**搜索二叉树的价值:**其实就是搜索和排序

1.1二叉搜索树的实现
对于二叉搜索树,和二叉树都一样需要定义一个二叉树节点,和二叉树本身
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
private:
Node* _root = nullptr;
};
1.1.1二叉搜索树的查找
1、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
2、最多查找高度次,走到到空,还没找到,这个值不存在。
// 二叉搜索树的查找
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return true;
}
}
// 走到这里说明,此时的cur走到了nullptr都没有找到,说明key不存在于该二叉搜索树中
return false;
}
1.1.2二叉搜索树的插入
思路:
- 判断根是否为空,空的话直接插入
- 根不为空,就根据二叉搜索树的性质去找空节点插入。
代码实现如下:
bool insert(const K& key)
{
// 先判断该树是否为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
// 让cur找到key要插入的位置(这个位置一定是nullptr)
Node* cur = _root;
Node* parent = nullptr;//双指针解决父节点和插入节点之间连接问题
while (cur)
{
// 判断key该往左还是右边走
// 判断完往那边走,记得让parent记住当前cur的位置,再让cur往下走
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 二叉搜索树不允许出现数据重复,因此遇到相同的数据不能插入
return false;
}
}
// 此时cur找到了一个空的可以插入的位置
cur = new Node(key);
// cur节点被创建出来之后,父节点要连接cur节点
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
测试代码:
void testBSTree()
{
BSTree<int> tree;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
tree.insert(e);
}
}
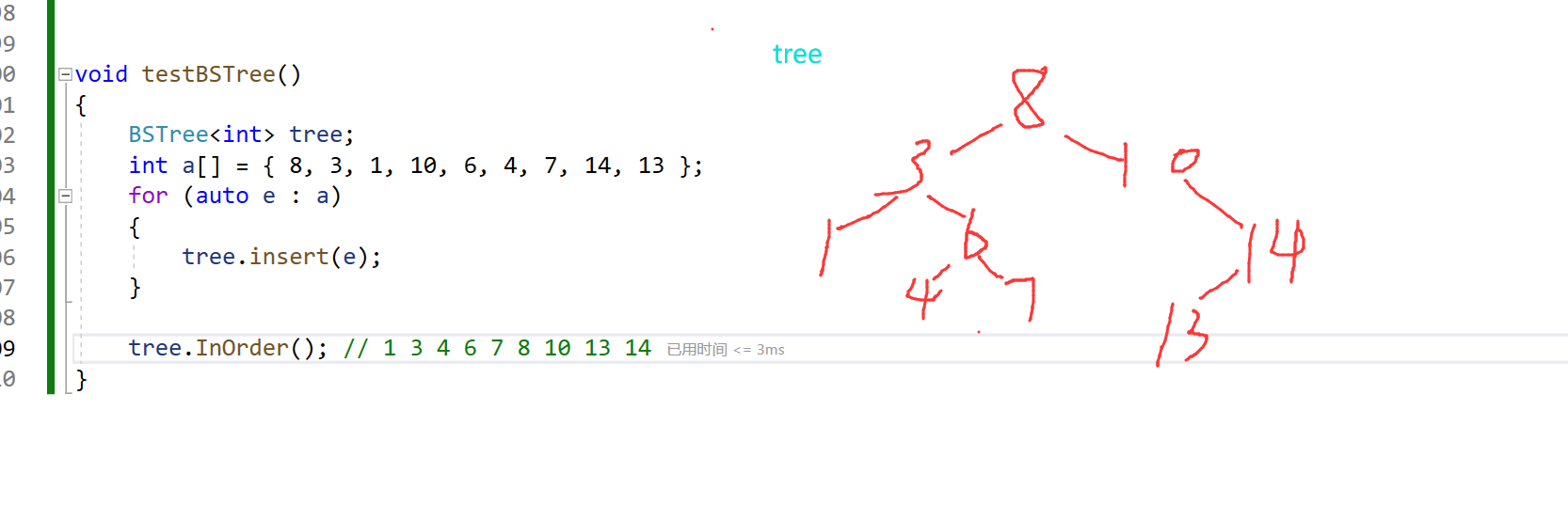
1.1.3中序遍历(排序)
在二叉搜索树当中,如果用中序遍历,恰好就是升序排序的结果。这也是为什么二叉搜索树又被叫做二叉排序树的原因。
代码如下:
// 中序遍历
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
//cpp中一般实现递归都要通过子函数
// 因为外边调用这个中序遍历接口的时候没办法直接传一个_root进来,_root是私有的
void InOrder()
{
_InOrder(_root);
//_InOrder(this->_root); // 等价于上面的
cout << endl;
}
测试代码:
BSTree<int> tree;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
tree.insert(e);
}
tree.InOrder(); // 1 3 4 6 7 8 10 13 14
1.1.4二叉搜索树的删除(重点)
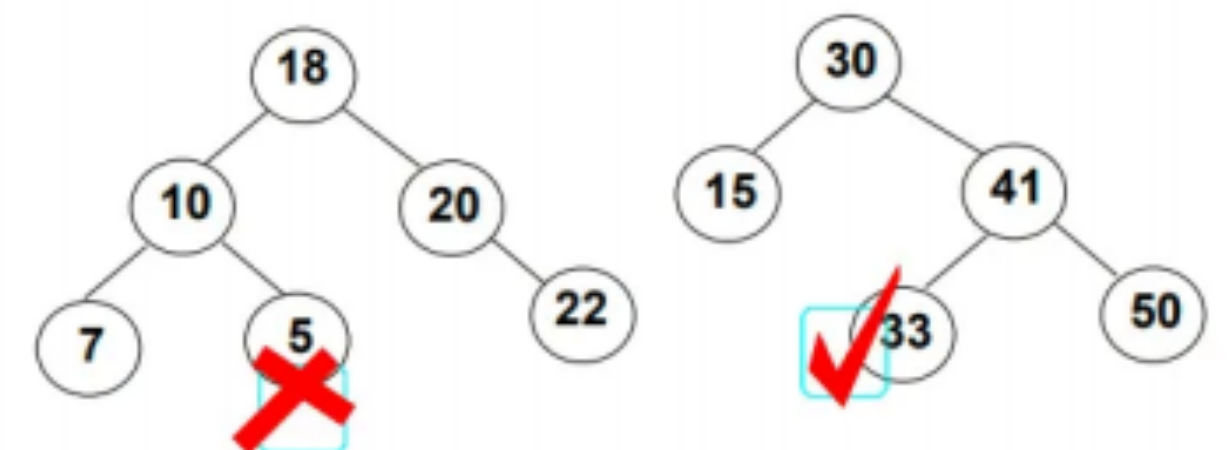
正常来说一共会有四种情况,但是我们可以归为3类,如下图所示:

对于只有左孩子的情况,还需要分类讨论:
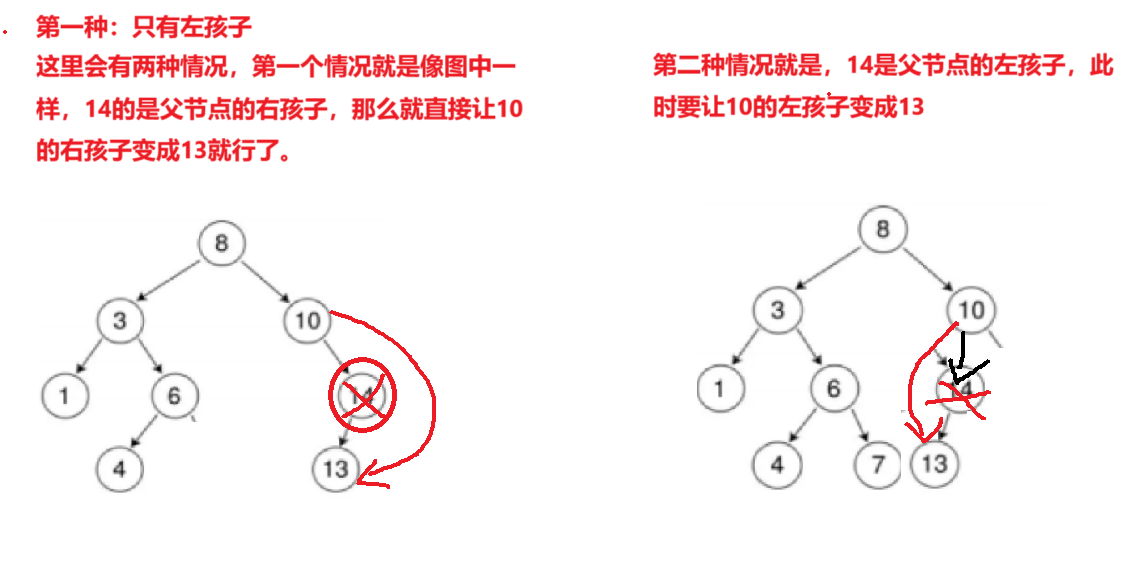
只有右孩子的情况也要分类讨论:
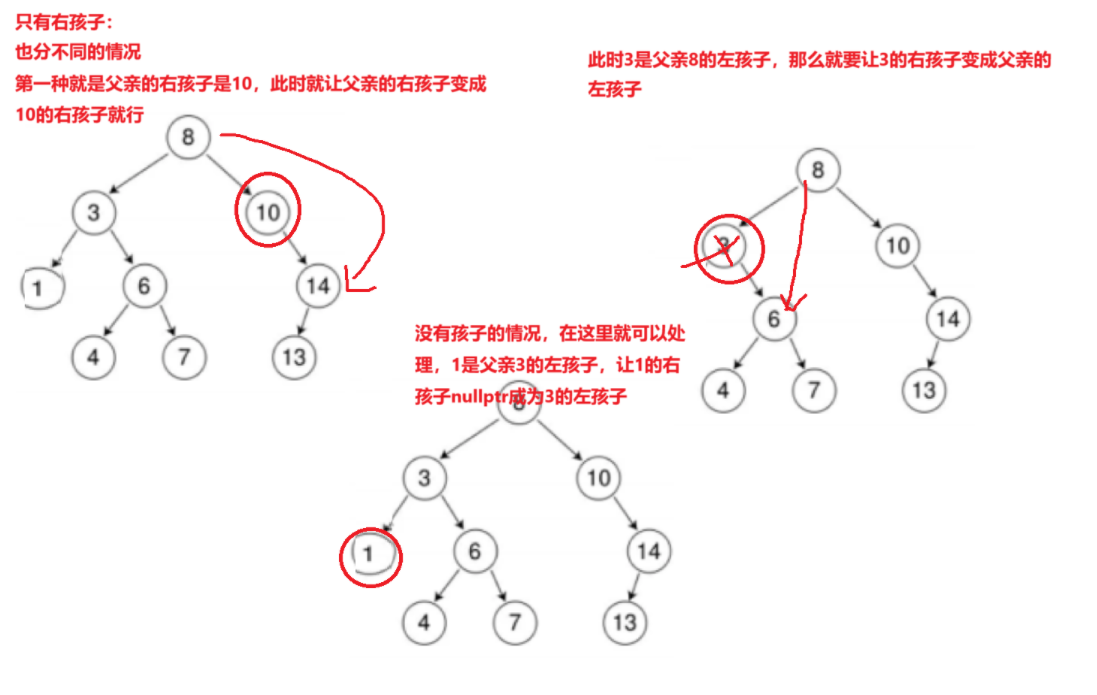
两个孩子都有的情况是不同的,需要用到替换法:
找左子树的最大节点或者找右子树的最小节点
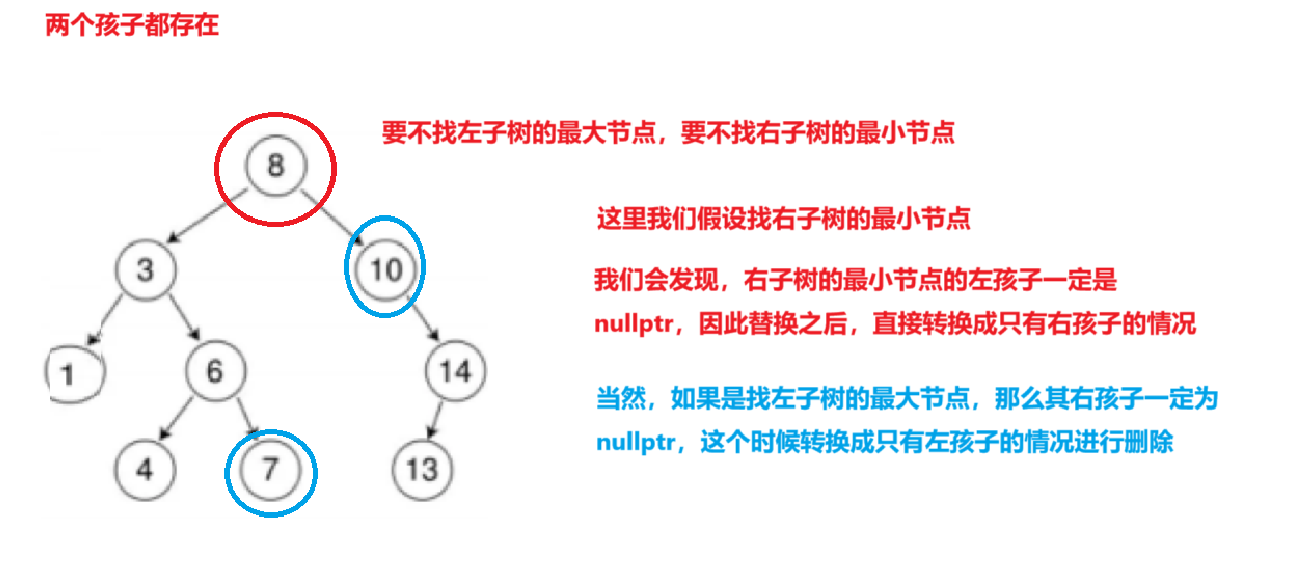
代码实现如下:
// 二叉搜索树的删除
bool Erase(const K& key)
{
// 传了个空树就不用删除了
if (_root == nullptr)
return false;
// 仍然采用双指针来连接父节点和新的孩子节点
Node* parent = nullptr;
Node* cur = _root;
// 先找到key的位置
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 此时就是找到了key的位置,开始判断key所在的节点是那种情况
//1.只有左孩子
//2.只有右孩子
//3.双孩子节点
//1.只有左孩子
if (cur->_right == nullptr)
{
// 这里有个特殊情况,当删除的是只有左孩子的根节点时,下面会对parent的nullptr值解引用,报错、
// 因此进行特殊处理
if (_root == cur)
{
_root = cur->_left;
delete cur;
cur = nullptr;
return true;
}
// 只有左孩子的情况下,还有两种情况需要分类讨论
//1.cur是父节点的左孩子
if (parent->_left == cur)
{
// 此时让cur的左孩子变成父节点的左孩子
parent->_left = cur->_left;
}
else//2.cur是父节点的右孩子
{
// cur的左孩子成为父节点的右孩子
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
}
else if (cur->_left == nullptr) // 2.只有右孩子
{
// 这里有个特殊情况,当删除的是只有右孩子的根节点时,下面会对parent的nullptr值解引用,报错、
// 因此进行特殊处理
if (_root == cur)
{
// 直接让右孩子成为跟节点
_root = cur->_right;
delete cur;
cur = nullptr;
return true;
}
// 只有右孩子,还是有两种情况需要分类讨论
//1.cur是父节点的右孩子
if (parent->_right == cur)
{
// 让cur的右孩子变成父节点的右孩子
parent->_right = cur->_right;
}
else // 2.cur是父节点的左孩子
{
// 让cur的右孩子变成父节点的左孩子
parent->_left = cur->_right;
}
delete cur;
cur = nullptr; // 这里不重置会调用cur这个已经析构的空间
}
else // 3.两个孩子都存在
{
// 该情况要使用替换法
// 此时可以找左子树的最大节点或者是右子树的的最小节点
// 这里用右子树的最小节点替换cur
Node* rightMinParent = nullptr;
Node* rightMin = cur->_right;
// 这里不断的找右子树的最小节点
while (rightMin->_left) // 当找到左孩子为空时,该节点就是右子树最小的。
{
rightMinParent = rightMin;
rightMin = rightMin->_left;
}
//找到了之后要进行替换
cur->_key = rightMin->_key;
// 这里要排除,当右子树直接找到最小节点的时候,此时由于循环上面的循环没进去,rightMinParent没有赋值
// 如果直接进行下面的判断,会直接对nullptr进行解引用导致报错
if (rightMinParent == nullptr)
{
// 这种情况直接删除右孩子,就行了
cur->_right = rightMin->_right;
delete rightMin;
rightMin = nullptr;
return true;
}
// 此时要删除的节点转换到了rightMin上,这里就转换成了只有右孩子的情况(也可能是叶子节点,没有右孩子)
// 因此要进行分类讨论,这里和上面对只有右孩子情况的处理是一样的,就不多说
if (rightMinParent->_left == rightMin)
{
rightMinParent->_left = rightMin->_right;
}
else
{
rightMinParent->_right = rightMin->_right;
}
delete rightMin;
rightMin = nullptr;
return true;
}
}
}
// 走到这里就说明,key不存在
return false;
}
对于二叉搜索树有较多极端情况需要处理,因此需要对各种极端情况进行测试。
测试用例:
void testBSTree()
{
BSTree<int> tree;
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto e : a)
{
tree.insert(e);
}
// 测试二叉搜索树的删除(对4种情况的节点都进行测试)【实际上处理只分了三种情况】
tree.Erase(1);
tree.InOrder();
tree.Erase(14);
tree.InOrder();
tree.Erase(10);
tree.InOrder();
tree.Erase(8);
tree.InOrder();
tree.Erase(19);
tree.InOrder();
// 删空也要没问题才行
for (auto e : a)
{
tree.Erase(e);
tree.InOrder();
}
// 最好还要对两个特殊情况做测试:
// 1.只有左子树的树,删除跟节点的第一个左孩子
// 2.只有右子树的树,删除跟节点的第一个右孩子
for (auto e : a)
{
tree.insert(e);
}
tree.Erase(10);
tree.Erase(14);
tree.Erase(13);
// 此时该树是一个只有左孩子的树,删除3,即根节点第一个左孩子
tree.Erase(3);
tree.InOrder();
for (auto e : a)
{
tree.insert(e);
}
tree.Erase(3);
tree.Erase(1);
tree.Erase(6);
tree.Erase(4);
tree.Erase(7);
// 此时该树是一个只有右孩子的树,删10,即根节点第一个右孩子
tree.Erase(10);
tree.InOrder();
}
1.2二叉搜索树的应用
1.2.1K模型
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值
比如:有一个单词add,检查是否拼写正确。
就让其所有单词构建一个二叉搜索树,然后再这个树里找add存不存在,不存在就说明拼写错误。
前面实现的二叉搜索树就是K模型
1.2.2KV模型
- KV模型:每一个关键码Key,都有与之对应的值Value,也就是<Key,Value>键值对
这个KV模型在现实生活中非常常见:
- 比如高铁站通过身份证来验证你是否购买了票。
验证时就是读取你的身份证号码,在二叉搜索树中寻找你的号码是否存在,存在了之后去找你是否购买了票。最后还要在加一个人脸识别的验证。
在这里身份证号码就是Key,票就是Value。<身份证号码,票>构成Value
- 英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对
- 统计次数
KV模型下的二叉搜索树的代码实现:
其实这个没和K模型的代码实现没什么区别。
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
// 二叉搜索树的查找
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
// 走到这里说明,此时的cur走到了nullptr都没有找到,说明key不存在于该二叉搜索树中
return nullptr;
}
// 二叉搜索树的插入
bool insert(const K& key, const V& value)
{
// 先判断该树是否为空
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
// 让cur找到key要插入的位置(这个位置一定是nullptr)
Node* cur = _root;
Node* parent = nullptr;//双指针解决父节点和插入节点之间连接问题
while (cur)
{
// 判断key该往左还是右边走
// 判断完往那边走,记得让parent记住当前cur的位置,再让cur往下走
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 二叉搜索树不允许出现数据重复,因此遇到相同的数据不能插入
return false;
}
}
// 此时cur找到了一个空的可以插入的位置
cur = new Node(key, value);
// cur节点被创建出来之后,父节点要连接cur节点
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
// 二叉搜索树的删除
bool Erase(const K& key)
{
// 传了个空树就不用删除了
if (_root == nullptr)
return false;
// 仍然采用双指针来连接父节点和新的孩子节点
Node* parent = nullptr;
Node* cur = _root;
// 先找到key的位置
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 此时就是找到了key的位置,开始判断key所在的节点是那种情况
//1.只有左孩子
//2.只有右孩子
//3.双孩子节点
//1.只有左孩子
if (cur->_right == nullptr)
{
// 这里有个特殊情况,当删除的是只有左孩子的根节点时,下面会对parent的nullptr值解引用,报错、
// 因此进行特殊处理
if (_root == cur)
{
_root = cur->_left;
delete cur;
cur = nullptr;
return true;
}
// 只有左孩子的情况下,还有两种情况需要分类讨论
//1.cur是父节点的左孩子
if (parent->_left == cur)
{
// 此时让cur的左孩子变成父节点的左孩子
parent->_left = cur->_left;
}
else//2.cur是父节点的右孩子
{
// cur的左孩子成为父节点的右孩子
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
}
else if (cur->_left == nullptr) // 2.只有右孩子
{
// 这里有个特殊情况,当删除的是只有右孩子的根节点时,下面会对parent的nullptr值解引用,报错、
// 因此进行特殊处理
if (_root == cur)
{
// 直接让右孩子成为跟节点
_root = cur->_right;
delete cur;
cur = nullptr;
return true;
}
// 只有右孩子,还是有两种情况需要分类讨论
//1.cur是父节点的右孩子
if (parent->_right == cur)
{
// 让cur的右孩子变成父节点的右孩子
parent->_right = cur->_right;
}
else // 2.cur是父节点的左孩子
{
// 让cur的右孩子变成父节点的左孩子
parent->_left = cur->_right;
}
delete cur;
cur = nullptr; // 这里不重置会调用cur这个已经析构的空间
}
else // 3.两个孩子都存在
{
// 该情况要使用替换法
// 此时可以找左子树的最大节点或者是右子树的的最小节点
// 这里用右子树的最小节点替换cur
Node* rightMinParent = nullptr;
Node* rightMin = cur->_right;
// 这里不断的找右子树的最小节点
while (rightMin->_left) // 当找到左孩子为空时,该节点就是右子树最小的。
{
rightMinParent = rightMin;
rightMin = rightMin->_left;
}
//找到了之后要进行替换
cur->_key = rightMin->_key;
// 这里要排除,当右子树直接找到最小节点的时候,此时由于循环上面的循环没进去,rightMinParent没有赋值
// 如果直接进行下面的判断,会直接对nullptr进行解引用导致报错
if (rightMinParent == nullptr)
{
// 这种情况直接删除右孩子,就行了
cur->_right = rightMin->_right;
delete rightMin;
rightMin = nullptr;
return true;
}
// 此时要删除的节点转换到了rightMin上,这里就转换成了只有右孩子的情况(也可能是叶子节点,没有右孩子)
// 因此要进行分类讨论,这里和上面对只有右孩子情况的处理是一样的,就不多说
if (rightMinParent->_left == rightMin)
{
rightMinParent->_left = rightMin->_right;
}
else
{
rightMinParent->_right = rightMin->_right;
}
delete rightMin;
rightMin = nullptr;
return true;
}
}
}
// 走到这里就说明,key不存在
return false;
}
// 中序遍历
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ": " << root->_value << " " << endl;
_InOrder(root->_right);
}
//cpp中一般实现递归都要通过子函数
// 因为外边调用这个中序遍历接口的时候没办法直接传一个_root进来,_root是私有的
void InOrder()
{
if (_root == nullptr)
{
cout << "该树为空" << endl;
return;
}
_InOrder(_root);
//_InOrder(this->_root); // 等价于上面的
cout << endl;
}
private:
Node* _root = nullptr;
};
KV模型的应用:
- 中英互译的词典<word, chinese>
// 这里的Key除了是int类型,还可以是其他类型,只要这个类型能够支持比较大小就OK
BSTree<string, string> dict;
dict.insert("sort", "排序");
dict.insert("string", "字符串");
dict.insert("tree", "树");
dict.insert("people", "人");
dict.InOrder();
string str;
cout << "输入你要查找的单词:";
while (cin >> str)
{
BSTreeNode<string, string>* ret = dict.Find(str);
if (ret) // 只要返回的不是nullptr就说明找到了
{
cout << str<< ": " << ret->_value << endl;
}
else
{
cout << "找不到该单词\n";
}
}

- 统计次数
// 下面是一个二叉搜索树非常善于做的事情
// 现在有个需求:统计下面字符串出现的次数
string strArr[] = { "苹果", "苹果", "苹果", "苹果", "苹果", "橘子", "橘子", "橘子", "香蕉" };
BSTree<string, int> countTree;
for (auto str : strArr)
{
BSTreeNode<string, int>* ret = countTree.Find(str);
if (ret)
{
// 已经存在了就++
ret->_value++;
}
else
{
// 不存在就插入
countTree.insert(str, 1);
}
}
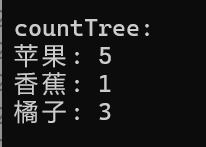
cout << "countTree:\n";
countTree.InOrder();
1.3二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
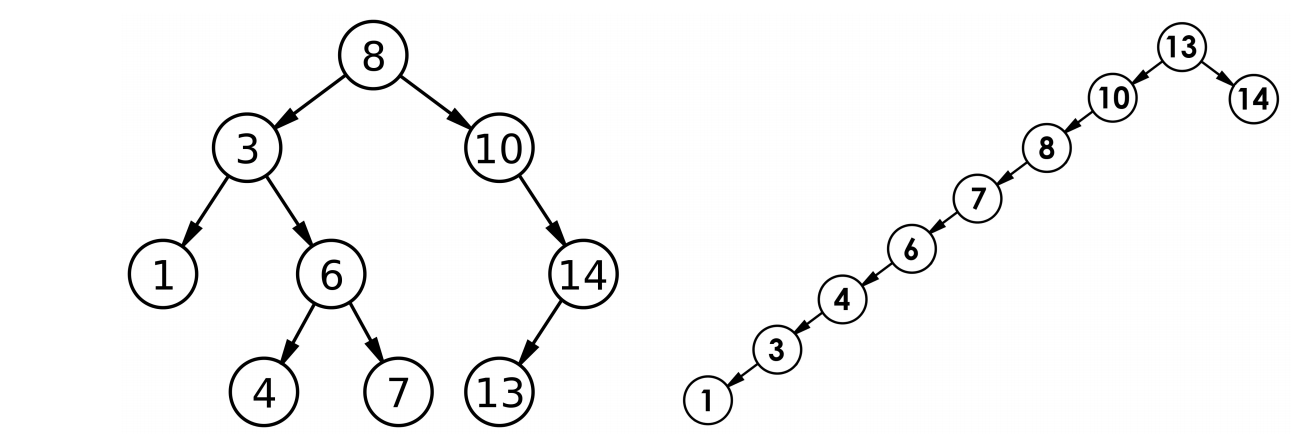
可以看到,二叉搜索树的结构可能会偏向极端,如右图所示
在最好的情况下——二叉搜索树接近完全二叉树,此时的平均比较次数就是以2为底的log(N)
在最坏的情况下——二叉搜索树接近单支数,此时的平均比较次数就是N/2。
在最坏的情况下,此时的效率就和链表和顺序表那些数据结构没有区别了、
因此,对于这种情况下,解决办法就是——平衡树
- AVLTree
- 红黑树
这两个数据结构属于高阶的数据结构
苹果", “橘子”, “橘子”, “橘子”, “香蕉” };
BSTree<string, int> countTree;
for (auto str : strArr)
{
BSTreeNode<string, int>* ret = countTree.Find(str);
if (ret)
{
// 已经存在了就++
ret->_value++;
}
else
{
// 不存在就插入
countTree.insert(str, 1);
}
}
cout << “countTree:\n”;
countTree.InOrder();
[外链图片转存中...(img-nBO6tRwJ-1727020957466)]
### 1.3二叉搜索树的性能分析
**插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能**
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即**结点越深,则比较次数越多。**
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
[外链图片转存中...(img-2lVnlFof-1727020957466)]
可以看到,二叉搜索树的结构可能会偏向极端,如右图所示
**在最好的情况下——二叉搜索树接近完全二叉树,此时的平均比较次数就是以2为底的log(N)**
**在最坏的情况下——二叉搜索树接近单支数,此时的平均比较次数就是N/2。**
在最坏的情况下,此时的效率就和链表和顺序表那些数据结构没有区别了、
因此,对于这种情况下,解决办法就是——**平衡树**
1. AVLTree
2. 红黑树
这两个数据结构属于高阶的数据结构