文章目录
- 多源BFS
- 542. 01 矩阵
- 题目解析
- 算法原理
- 代码实现
- 1020. 飞地的数量
- 题目解析
- 算法原理
- 1765. 地图中的最高点
- 题目解析
- 算法原理
- 代码实现
- 1162. 地图分析
- 题目解析
- 算法原理
- 代码实现
多源BFS
单源最短路: 一个起点、一个终点
多源最短路: 可以多个起点,一个终点
多源BFS: 用BFS解决边权为1的多源最短路(😂)
BFS 解决边权为1的最短路问题
如何解决:
- 解法一:暴力枚举,把多源最短路转换成若干个单源最短路(大概率超时)
- 解法二:把所有源点当成一个“超级源点”,问题就变成了单一的单源最短路问题
想办法将若干个起点,当作一个起点
为什么正确? 如图:
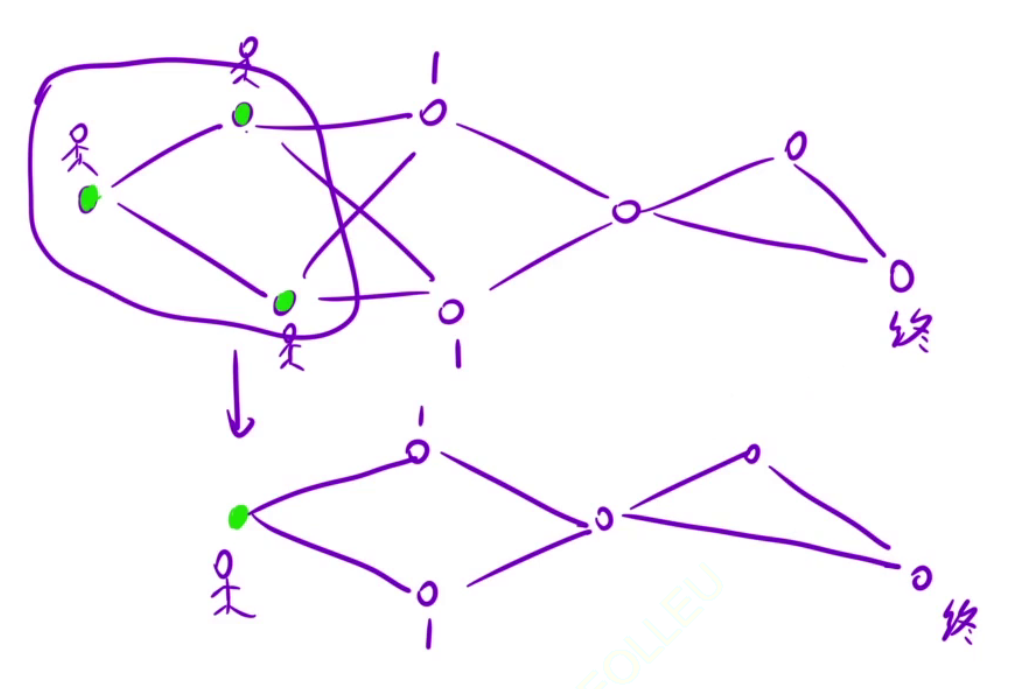
如何代码实现:
- 所有起点加入到队列当中
- 一层一层向外扩展
542. 01 矩阵
题目链接:542. 01 矩阵
题目解析
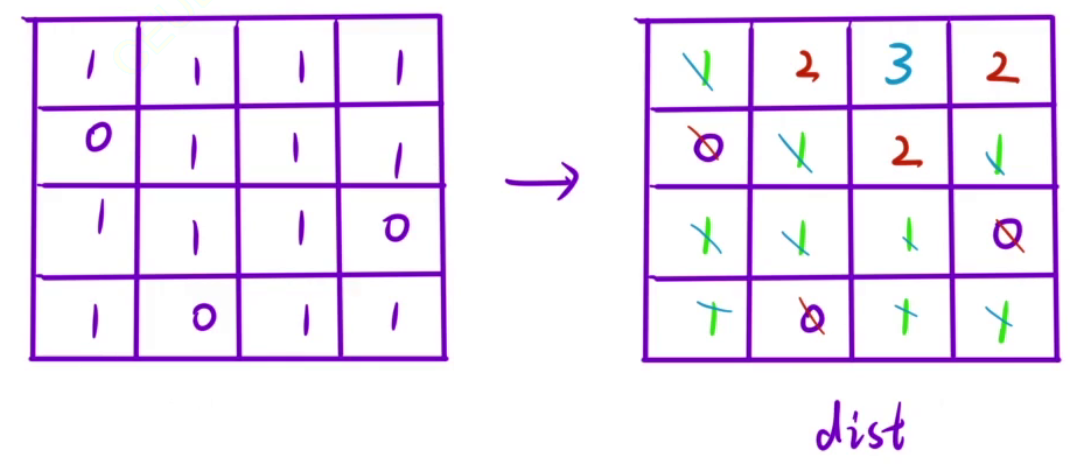
给我们一个矩阵,矩阵由0和1组成
要我们返回的也是一个矩阵,里面放的是每个位置里0最近的距离
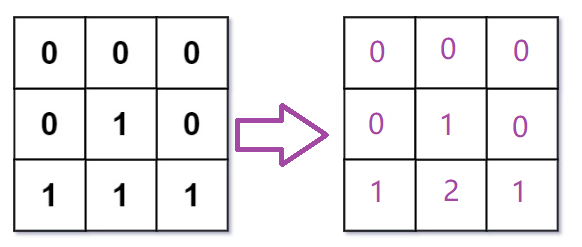
算法原理
- 把所有的0当成起点,1当成终点
- 将所有
0位置加入队列 - 一层一层向外扩展
代码实现
class Solution {
public:
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
vector<vector<int>> updateMatrix(vector<vector<int>>& mat)
{
int m = mat.size();
int n = mat[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(mat[i][j] == 0)
{
q.push({i, j});
dist[i][j] = 0;
}
}
}
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; k++)
{
int x = dx[k] + a;
int y = dy[k] + b;
if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}
};
1020. 飞地的数量
题目链接:1020. 飞地的数量
题目解析
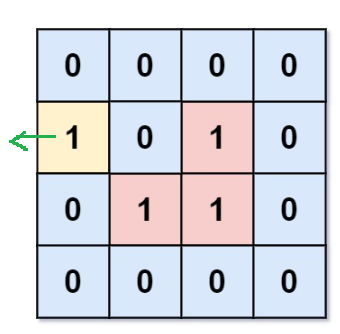
给我们一个矩阵,由0和1组成,1表示陆地,0表示海洋
要我们求出,无法“上岸”数量
算法原理
正难则反:
直接看四个边界,是否有“陆地”
如果有,直接往里面搜索,看有多少连在一起的
class Solution {
public:
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int numEnclaves(vector<vector<int>>& grid)
{
int m = grid.size();
int n = grid[0].size();
vector<vector<bool>> vis(m, vector<bool>(n));
queue<pair<int, int>> q;
//四周 1 加入队列
for(int j = 0; j < n; j++)
{
if(grid[0][j] == 1)
{
q.push({0, j});
vis[0][j] = true;
}
if(grid[m-1][j] == 1)
{
q.push({m-1, j});
vis[m-1][j] = true;
}
}
for(int i = 0; i < m; i++)
{
if(grid[i][0] == 1)
{
q.push({i, 0});
vis[i][0] = true;
}
if(grid[i][n - 1] == 1)
{
q.push({i, n-1});
vis[i][n-1] = true;
}
}
//多源bfs
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; k++)
{
int x = dx[k] + a;
int y = dy[k] + b;
if(x >= 0 && y >= 0 && x < m && y < n && grid[x][y] == 1 && !vis[x][y])
{
vis[x][y] = true;
q.push({x, y});
}
}
}
int ret = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == 1 && !vis[i][j]) ret++;
}
}
return ret;
}
};
1765. 地图中的最高点
题目链接:1765. 地图中的最高点
题目解析
给我们一个矩阵,由陆地和水域组成
isWater[i][j] == 0为陆地isWater[i][j] == 1为水域
规则如下:
- 格子高度非负
- 格子为水域,高度为0
- 相邻格子,高度差不大于1
最终要得出,怎么排列,能得到让最高的高度最大。
算法原理
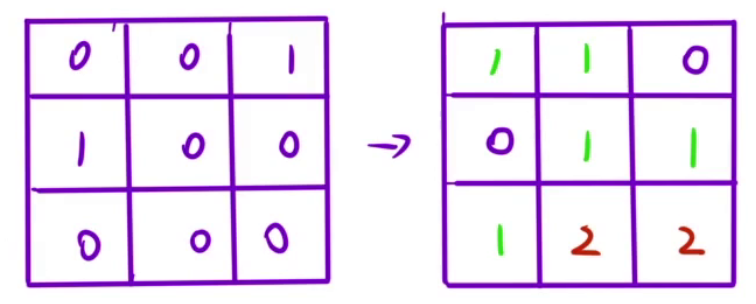
- 这里最先排列的肯定是水域,如果是水域,设置为
0,即先遍历矩阵,将水域格子加入队列 - 然后一层一层向外扩展
代码实现
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
vector<vector<int>> highestPeak(vector<vector<int>>& isWater)
{
int m = isWater.size();
int n = isWater[0].size();
vector<vector<int>> dist(m,vector<int>(n, -1));
queue<pair<int, int>> q;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(isWater[i][j] == 1)
{
dist[i][j] = 0;
q.push({i, j});
}
}
}
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; k++)
{
int x = dx[k] + a;
int y = dy[k] + b;
if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}
};
1162. 地图分析
题目链接:1162. 地图分析
题目解析
给我一个矩阵,0和1组成
0表示海洋1表示陆地
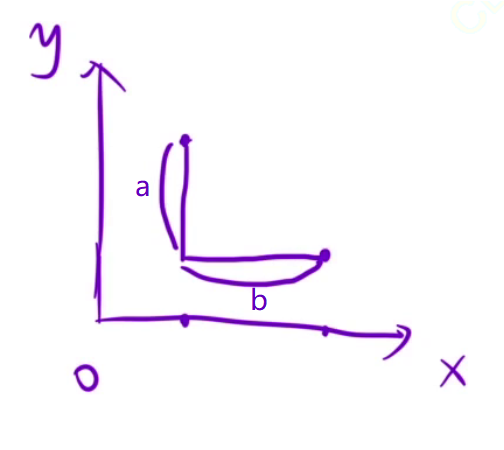
要我们找出海洋离陆地的最大距离(曼哈顿距离, a+b)
算法原理
反过来,陆地到海洋的距离,一层一层往外扩
- 陆地加入队列,此时距离为1
- 往外扩展
代码实现
class Solution {
public:
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0 ,0};
int maxDistance(vector<vector<int>>& grid)
{
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == 1)
{
dist[i][j] = 0;
q.push({i, j});
}
}
}
int ret = -1;
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; k++)
{
int x = dx[k] + a;
int y = dy[k] + b;
if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
ret = dist[x][y];
}
}
}
return ret;
}
};