LeetCode从入门到超凡（二）递归与分治算法

head-bar

引言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档；在算法设计中，递归和分治算法是两种非常重要的思想和方法。它们不仅在解决复杂问题时表现出色，而且在许多经典算法中都有广泛的应用😉。因此理解这两种算法的原理和思路，对算法学习很有意义！💕💕😊

介绍

递归（Recursion）：是一种通过重复将原问题分解为同类的子问题来解决问题的方法。在编程中，递归通常通过在函数内部调用函数自身来实现。递归算法的核心思想是将复杂问题分解为更小的子问题，直到子问题足够简单，可以直接求解。
递归算法在许多场景中都非常有用，例如树的遍历、图的搜索、以及一些数学问题的求解（如阶乘、斐波那契数列等）。

分治算法（Divide and Conquer）：是一种将复杂问题分解为多个相同或相似的子问题，直到子问题可以直接求解，再将子问题的解合并为原问题的解的方法。分治算法的核心思想是将问题分解为更小的子问题，递归地解决这些子问题，然后将子问题的解合并以得到原问题的解。分治算法在许多经典算法中都有应用，例如归并排序、快速排序、二分查找等。

🙂接下来，作者将和各位分别详细探讨递归算法和分治算法的基本原理和实现步骤。

一. 递归算法

1.简介

递归（Recursion） 是一种通过重复将原问题分解为同类的子问题来解决问题的方法。在编程中，递归通常通过在函数内部调用函数自身来实现。递归算法的核心思想是将复杂问题分解为更小的子问题，直到子问题足够简单，可以直接求解。递归算法在许多场景中都非常有用，例如树的遍历、图的搜索、以及一些数学问题的求解（如阶乘、斐波那契数列等）。

举例说明：阶乘计算的递归实现

让我们从一个经典的例子开始——阶乘计算。阶乘的数学定义如下：

$\text{fact}(n) = \begin{cases} 1 & \text{n = 0} \\ n \times \text{fact}(n - 1) & \text{n > 0} \end{cases}$

根据这个定义，我们可以使用递归来实现阶乘函数。代码如下：

def fact(n):
    if n == 0:
        return 1
    return n * fact(n - 1)

以 ( n = 6 ) 为例，上述代码中阶乘函数 $\text{fact}(6)$ 的计算过程如下：

fact(6)
= 6 * fact(5)
= 6 * (5 * fact(4))
= 6 * (5 * (4 * fact(3)))
= 6 * (5 * (4 * (3 * fact(2))))
= 6 * (5 * (4 * (3 * (2 * fact(1)))))
= 6 * (5 * (4 * (3 * (2 * (1 * fact(0))))))
= 6 * (5 * (4 * (3 * (2 * (1 * 1)))))
= 6 * (5 * (4 * (3 * (2 * 1))))
= 6 * (5 * (4 * (3 * 2)))
= 6 * (5 * (4 * 6))
= 6 * (5 * 24)
= 6 * 120
= 720

这个过程就像是一个不断缩小的俄罗斯套娃，最终找到最小的那个。

2 递归的基本思想

① 递推过程：将问题分解为子问题

递归的递推过程是指将原问题分解为更小的子问题。在这个过程中，函数会不断调用自身，直到达到某个终止条件。例如，在阶乘计算中，我们将 $\text{fact}(n)$ 分解为 $\times \text{fact}(n - 1)$ 。

② 回归过程：从子问题的解回归到原问题的解

回归过程是指从最小的子问题的解开始，逐步返回到原问题的解。在阶乘计算中，当 ( n = 0 ) 时，递归终止，开始回归过程，逐层返回结果，直到返回原问题的解。

③ 图示说明递推和回归过程

为了更直观地理解递推和回归过程，我们可以通过图示来说明。假设我们要计算 $\text{fact}(5)$ ，递推和回归过程如下图所示：

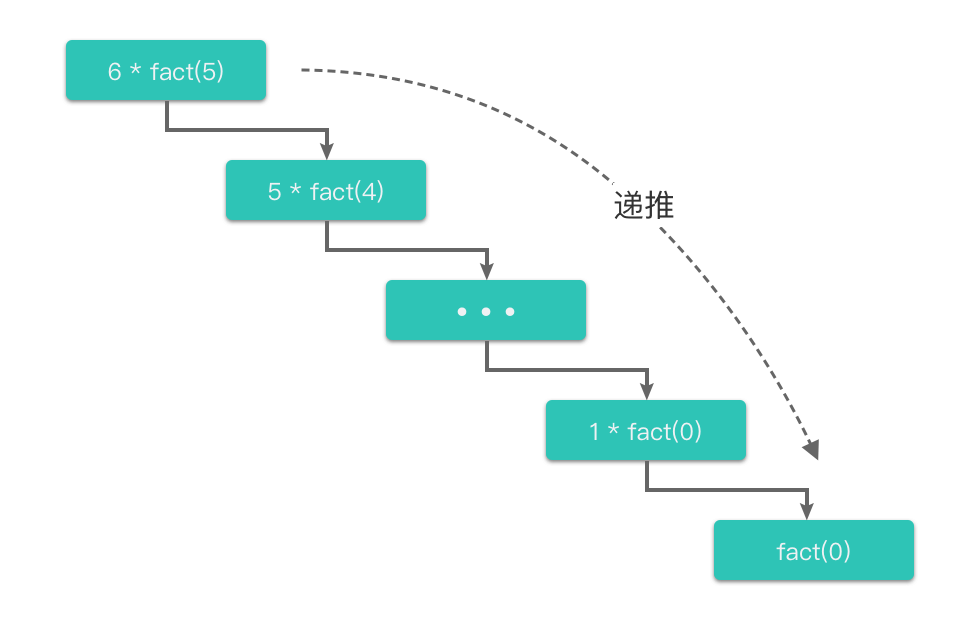
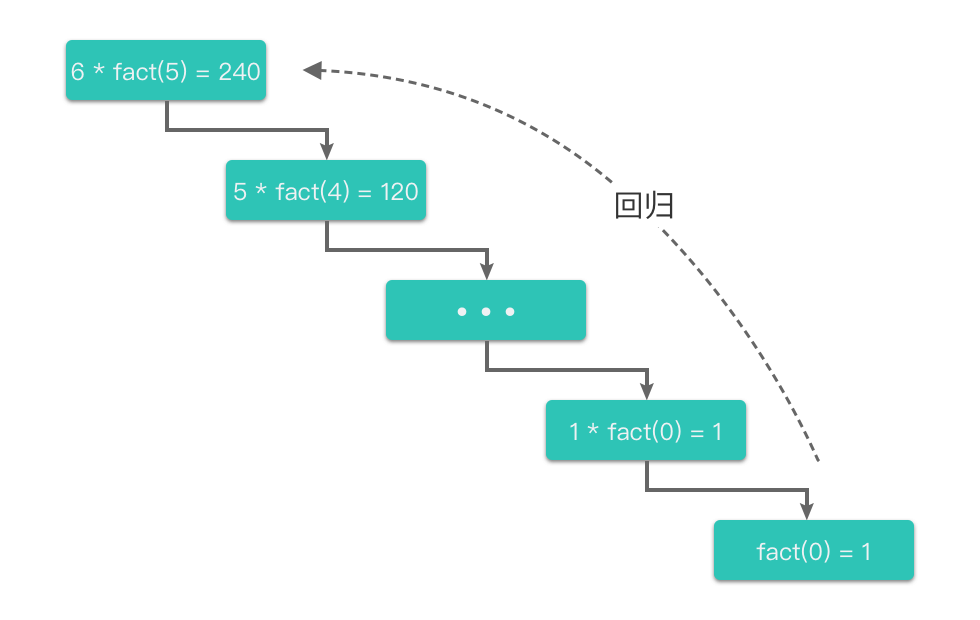
递归就像是一个不断重复的自我召唤过程，就像你在镜子前放了一面镜子，镜子里又有一个镜子，无限循环下去。在编程中，递归就是函数调用自身，直到问题变得足够简单，可以直接解决。

其基本思想就是：把规模大的问题不断分解为子问题来解决。

3. 递归与数学归纳法

递归与数学归纳法的相似性

递归和数学归纳法在思想上非常相似。数学归纳法是一种证明方法，通常用于证明某个命题对所有自然数成立。数学归纳法的证明步骤如下：

基例：证明当 n = b 时，命题成立。
归纳步骤：假设当 n = k 时命题成立，证明当 ( n = k + 1 ) 时命题也成立。

递归的实现过程也可以分为两个部分：

递归终止条件：相当于数学归纳法中的基例。
递推过程：相当于数学归纳法中的归纳步骤。

数学归纳法的证明步骤与递归的对应关系

递归终止条件：数学归纳法第一步中的 ( n = b )，可以直接得出结果。
递推过程：数学归纳法第二步中的假设部分（假设 ( n = k ) 时命题成立），也就是假设我们当前已经知道了 ( n = k ) 时的计算结果。
回归过程：数学归纳法第二步中的推论部分（根据 ( n = k ) 推论出 ( n = k + 1 )），也就是根据下一层的结果，计算出上一层的结果。

4 递归三步走

① 写出递推公式：找到将原问题分解为子问题的规律

写出递推公式的关键在于找到将原问题分解为子问题的规律，并将其抽象成递推公式。例如，在阶乘计算中，递推公式为 $\text{fact}(n) = n \times \text{fact}(n - 1)$ 。

② 明确终止条件：确定递归的结束条件

递归的终止条件也叫做递归出口。如果没有递归的终止条件，函数就会无限地递归下去，程序就会失控崩溃。通常情况下，递归的终止条件是问题的边界值。例如，在阶乘计算中，终止条件是 ( n = 0 )。

③ 将递推公式和终止条件翻译成代码

在写出递推公式和明确终止条件之后，我们就可以将其翻译成代码了。这一步也可以分为三步来做：

定义递归函数：明确函数意义、传入参数、返回结果等。
书写递归主体：提取重复的逻辑，缩小问题规模。
明确递归终止条件：给出递归终止条件，以及递归终止时的处理方法。

def fact(n):
    if n == 0:
        return 1
    return n * fact(n - 1)

5 注意事项

① 避免栈溢出：限制递归深度或转换为非递归算法

在程序执行中，递归是利用堆栈来实现的。每一次递推都需要一个栈空间来保存调用记录，每当进入一次函数调用，栈空间就会加一层栈帧。每一次回归，栈空间就会减一层栈帧。由于系统中的栈空间大小不是无限的，所以，如果递归调用的次数过多，会导致栈空间溢出。

为了避免栈溢出，我们可以在代码中限制递归调用的最大深度来解决问题。当递归调用超过一定深度时（比如 100）之后，不再进行递归，而是直接返回报错。当然，这种做法并不能完全避免栈溢出，也无法完全解决问题，因为系统允许的最大递归深度跟当前剩余的栈空间有关，事先无法计算。

如果使用递归算法实在无法解决问题，我们可以考虑将递归算法变为非递归算法（即递推算法）来解决栈溢出的问题。

② 避免重复运算：使用缓存（哈希表、集合或数组）保存已求解的子问题结果

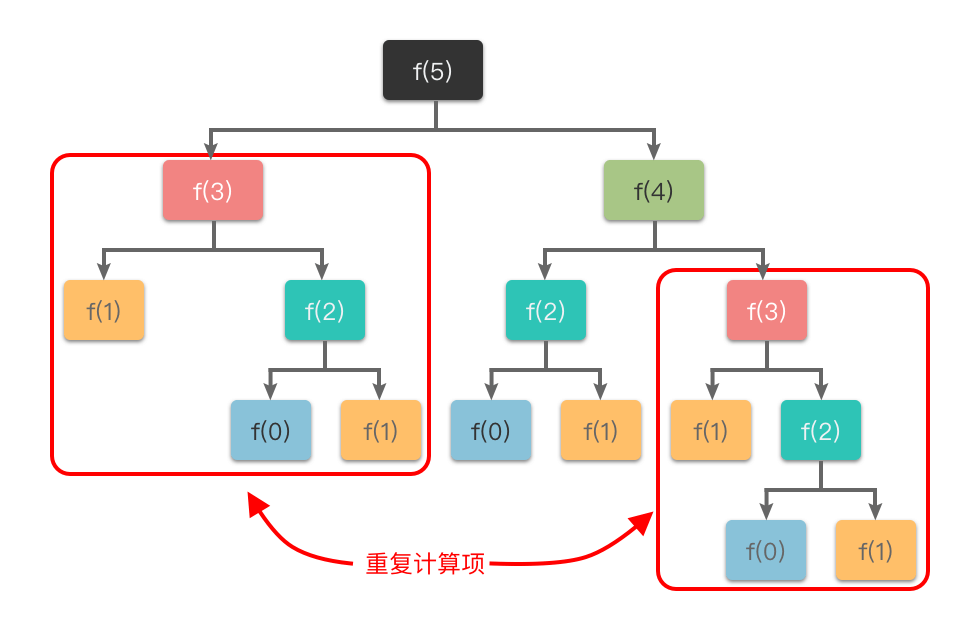
在使用递归算法时，还可能会出现重复运算的问题。例如，在计算斐波那契数列时，递归过程中会多次计算相同的子问题，导致效率低下。为了避免重复计算，我们可以使用一个缓存（哈希表、集合或数组）来保存已经求解过的子问题的结果。当递归调用到某个子问题时，先查看缓存中是否已经计算过结果，如果已经计算，则直接从缓存中取值返回，而无需继续递推，如此以来便避免了重复计算问题。

6.递归的应用

① 斐波那契数列：递归实现及其复杂度分析

斐波那契数列的定义如下：

$\begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ f(n - 1) + f(n - 2) & n > 1 \end{cases}$

我们可以使用递归来实现斐波那契数列的计算：

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n - 1) + fib(n - 2)

然而，这种递归实现的效率非常低，时间复杂度为 $ O(2^n) $，因为递归过程中会多次计算相同的子问题。为了避免重复计算，我们可以使用缓存来优化算法：

cache = {}
def fib(n):
    if n in cache:
        return cache[n]
    if n == 0:
        return 0
    if n == 1:
        return 1
    cache[n] = fib(n - 1) + fib(n - 2)
    return cache[n]

通过使用缓存，我们可以将时间复杂度降低到 ( O(n) )。

② 二叉树的最大深度：递归实现及其复杂度分析

二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。我们可以使用递归来计算二叉树的最大深度：

def maxDepth(root):
    if not root:
        return 0
    return max(maxDepth(root.left), maxDepth(root.right)) + 1

这个递归算法的时间复杂度为 ( O(n) )，其中 ( n ) 是二叉树的节点数。空间复杂度为 ( O(h) )，其中 ( h ) 是二叉树的高度。

二. 分治算法

1.简介

分治算法（Divide and Conquer）是一种经典的算法设计策略，其核心思想是**将一个复杂的问题分解为多个相同或相似的子问题，直到这些子问题变得足够简单，可以直接求解。然后，将这些子问题的解合并起来，形成原问题的解。**

分治算法的步骤通常包括以下三个部分：

分解（Divide）：将原问题分解为若干个规模较小的子问题，这些子问题通常是原问题的简化版本。
解决（Conquer）：递归地解决这些子问题。如果子问题的规模足够小，可以直接求解。
合并（Combine）：将子问题的解合并为原问题的解。

① 与递归的联系

递归是一种编程技巧，通过函数调用自身来解决问题。分治算法通常使用递归来实现，因为递归能够自然地表达问题的分解和合并过程。

具体来说，递归函数在执行过程中会不断地调用自身，直到达到某个基准条件（即子问题可以直接求解的条件），然后逐层返回结果，最终合并成原问题的解。

然而，分治算法并不局限于递归实现。在某些情况下，也可以使用迭代（循环）来实现分治策略。迭代实现通常需要手动管理问题的分解和合并过程，因此在复杂度上可能不如递归实现直观。

② 应用场景

分治算法广泛应用于各种领域，特别是在处理大规模数据或复杂问题时，其优势尤为明显。以下是一些常见的应用场景：

排序算法：如归并排序（Merge Sort）和快速排序（Quick Sort）。
搜索算法：如二分查找（Binary Search）。
矩阵运算：如矩阵乘法（Strassen算法）。
图算法：如最近公共祖先（LCA）问题。
几何问题：如最近点对问题。

③ 优缺点

优点：

高效性：通过将问题分解为多个子问题，分治算法通常能够显著降低问题的复杂度。
模块化：分治算法将问题分解为多个独立的子问题，便于模块化设计和实现。
可扩展性：分治算法适用于处理大规模问题，能够有效地利用多核处理器和分布式计算资源。

缺点：

递归开销：递归实现的分治算法可能会带来较大的函数调用开销，尤其是在问题规模较大时。
空间复杂度：递归实现通常需要额外的栈空间来存储中间结果，可能导致空间复杂度较高。
合并复杂度：在某些情况下，合并子问题的解可能比解决子问题本身更为复杂，导致整体效率下降。

2.适用条件

分治算法是一种强大的问题解决策略，但其适用性受到一些特定条件的限制。理解这些条件有助于我们在面对具体问题时，判断是否适合采用分治策略。这里作者整理了一下分治算法的应用条件：

② 可分解（Divisibility）

条件：问题可以分解为若干个规模较小的相同子问题。

解释：
分治算法的核心思想是将复杂问题分解为多个相同或相似的子问题。这意味着问题的结构必须允许我们将其划分为多个独立的子问题，且这些子问题的结构与原问题相同或相似。例如，在归并排序中，我们将一个数组分解为两个子数组，每个子数组的排序问题与原数组的排序问题结构相同。

思考：

可分解性是分治算法的基础。如果一个问题无法被自然地分解为多个子问题，或者分解后的子问题与原问题结构差异较大，那么分治算法可能不适用。
例如，某些非线性问题或依赖于全局信息的问题，可能不适合使用分治策略。
在实际应用中，我们需要分析问题的结构，判断其是否具有可分解性。

② 子问题可独立求解（Independence）

条件：子问题之间不包含公共的子子问题。

解释：
分治算法要求子问题之间是独立的，即每个子问题的求解不依赖于其他子问题的结果。如果子问题之间存在依赖关系，那么分治算法可能会变得复杂，甚至无法有效应用。例如，在快速排序中，每个子数组的排序是独立的，不依赖于其他子数组的排序结果。

思考：

子问题的独立性保证了我们可以并行地解决这些子问题，从而提高算法的效率。
如果子问题之间存在依赖关系，可能需要引入额外的数据结构或算法来处理这些依赖，这会增加问题的复杂度。
在实际应用中，我们需要分析子问题之间的关系，确保其独立性。

3. 具有分解的终止条件（Termination Condition）

条件：当问题的规模足够小时，能够用较简单的方法解决。

解释：
分治算法通过递归地分解问题，直到问题的规模足够小，可以直接求解。这个“足够小”的规模通常称为终止条件或基准条件。终止条件保证了递归过程能够终止，并且能够返回有效的结果。例如，在归并排序中，当子数组的长度为1时，可以直接返回该数组作为排序结果。

思考：

终止条件是分治算法的重要组成部分。如果问题无法被分解到足够小的规模，或者在终止条件下无法直接求解，那么分治算法可能无法正常工作。
例如，某些问题可能在分解到一定规模后，仍然需要复杂的计算才能求解，这会限制分治算法的应用。
在实际应用中，我们需要确定合适的终止条件，确保问题能够被有效分解和求解。

4. 可合并（Combinability）

条件：子问题的解可以合并为原问题的解，且合并操作的复杂度不能太高。

解释：
分治算法的最后一步是将子问题的解合并为原问题的解。合并操作的复杂度直接影响整体算法的效率。如果合并操作的复杂度过高，可能会抵消分解和求解子问题带来的效率提升。例如，在归并排序中，合并两个已排序的子数组的操作是线性的，复杂度较低。

思考：

合并操作的复杂度是分治算法的关键因素之一。在某些情况下，合并操作可能比求解子问题本身更为复杂，导致整体效率下降。
例如，某些问题的合并操作可能涉及复杂的计算或数据结构操作，这会增加算法的复杂度。
在实际应用中，我们需要仔细考虑合并操作的复杂度，确保其不会成为瓶颈。

3.应用案例:使用分治算法实现归并排序

① 代码

代码如下：

def merge_sort(arr):
    # 基本情况：如果数组长度小于等于1，直接返回数组
    if len(arr) <= 1:
        return arr
    
    # 分解：将数组分为两个子数组
    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]
    
    # 递归调用，分别对左右两个子数组进行排序
    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)
    
    # 合并：将两个有序的子数组合并为一个有序数组
    return merge(left_half, right_half)

def merge(left, right):
    # 定义一个空列表，用于存储合并后的有序数组
    merged_arr = []
    i = j = 0
    
    # 比较左右两个子数组的元素，按顺序合并到merged_arr中
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged_arr.append(left[i])
            i += 1
        else:
            merged_arr.append(right[j])
            j += 1
    
    # 将剩余的元素添加到merged_arr中
    merged_arr.extend(left[i:])
    merged_arr.extend(right[j:])
    
    return merged_arr

# 测试代码
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print("排序后的数组:", sorted_arr)

② 思路

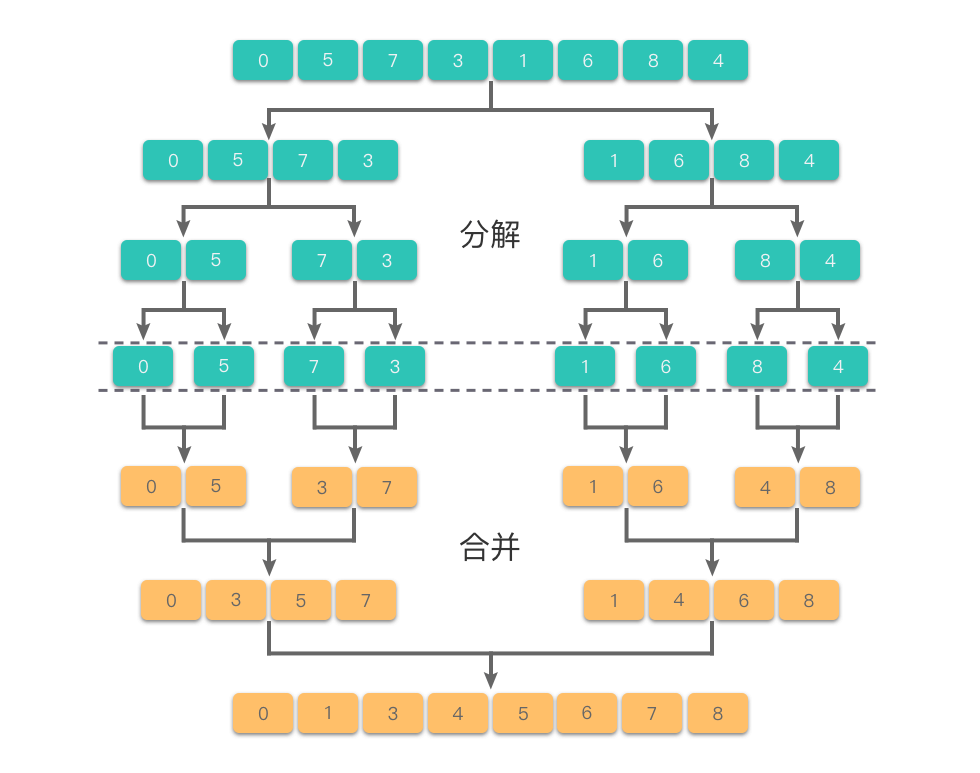
函数定义

def merge_sort(arr):

函数定义：merge_sort(arr) 是一个递归函数，用于对数组 arr 进行归并排序。

基本情况

if len(arr) <= 1:
    return arr

基本情况：当数组长度小于等于1时，直接返回数组。这是递归的终止条件，确保递归过程能够终止。

分解

mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]

分解：将数组 arr 分为两个子数组 left_half 和 right_half。mid 是数组的中间位置，left_half 包含前半部分元素，right_half 包含后半部分元素。

递归调用

left_half = merge_sort(left_half)
right_half = merge_sort(right_half)

递归调用：递归调用 merge_sort 函数，分别对左右两个子数组进行排序。

合并

return merge(left_half, right_half)

合并：调用 merge 函数，将两个有序的子数组合并为一个有序数组，并返回合并后的结果。

合并函数

def merge(left, right):
    merged_arr = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged_arr.append(left[i])
            i += 1
        else:
            merged_arr.append(right[j])
            j += 1
    
    merged_arr.extend(left[i:])
    merged_arr.extend(right[j:])
    
    return merged_arr

合并函数：merge(left, right) 函数用于将两个有序的子数组 left 和 right 合并为一个有序数组。

- **初始化**：定义一个空列表 `merged_arr`，用于存储合并后的有序数组。
- **比较与合并**：使用两个指针 `i` 和 `j`，分别指向 `left` 和 `right` 的当前元素。比较两个指针指向的元素，将较小的元素添加到 `merged_arr` 中，并将对应指针后移。
- **剩余元素**：将 `left` 和 `right` 中剩余的元素添加到 `merged_arr` 中。
- **返回结果**：返回合并后的有序数组 `merged_arr`。

测试代码

arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print("排序后的数组:", sorted_arr)

测试代码：定义一个测试数组 arr，调用 merge_sort 函数对其进行排序，并输出排序后的结果。

③ 思维导图

lct2

三、总结

这里我们发现递归和分治算法思路很相似，我们再次声明一下其区别与联系，帮助读者更好的理解；

递归是一种编程技巧，通过函数调用自身来简化问题的求解过程。
分治算法是一种算法设计策略，通过将复杂问题分解为多个简单的子问题，并递归地解决这些子问题，最终合并得到原问题的解。
递归是实现分治算法的一种常用方法，但递归的应用范围更广，不仅仅局限于分治算法。
分治算法是一种特定的算法设计策略，适用于那些可以被分解为多个相同或相似子问题的问题。