原题链接
一. 题目描述
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
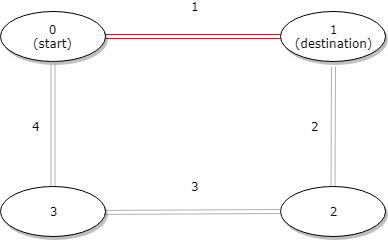
输入:distance = [1,2,3,4], start = 0, destination = 1 输出:1 解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
示例 2:
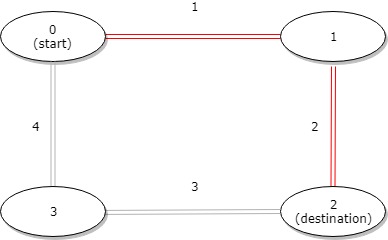
输入:distance = [1,2,3,4], start = 0, destination = 2 输出:3 解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
示例 3:
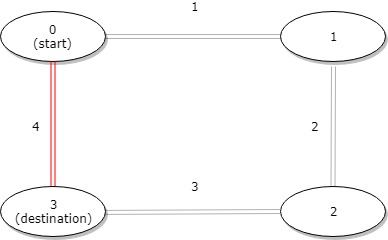
输入:distance = [1,2,3,4], start = 0, destination = 3 输出:4 解释:公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
二. 解题思路
本题也是非常简单的一题,给定你一个环形的公交车行驶路径,其中第i个位置的值等于从i 位置到 i + 1 位置的距离,给定你一个start 开始位置和destination 结束位置,让你判断从开始位置到结束位置的最短距离,即需要顺时针还是逆时针行驶;
我刚开始想到的是使用前缀和的思想实现,但是发现这个题没必要,只需要简单的遍历即可,我们首先得判断起始位置和终止位置的大小关系,如果start > destination ,就需要将他们之间进行一次调换(目的是计算顺时针所走的路径长度),然后开始遍历数组,如果当前的i 大于或等于 start 并且小于 destination ,说明该路径是我们顺时针行走的必行路径,将其加入到一个ans 中即可,然后在外侧使用一个sum 统计走完一圈的路径长度。
在结束循环之后我们只需要统计ans 和 sum - ans 的大小,选择最小的一个返回即可。
话不多说!!!上代码!!
三. 代码
class Solution {
public:
int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
int n = distance.size();
int ans = 0;
int sum = 0;
if(start > destination){
swap(start, destination);
}
for(int i = 0; i < n; i++){
if(i >= start && i < destination){
ans += distance[i];
}
sum += distance[i];
}
int res = min(ans, sum - ans);
return res;
}
};四. 总结
时间复杂度:O(n);
空间复杂度:O(1)。