数据选择器实现逻辑电路

描述

请使用此4选1数据选择器和必要的逻辑门实现下列表达式。

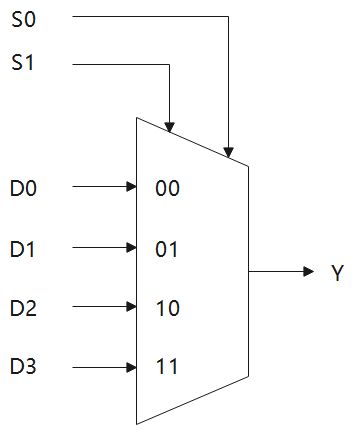
数据选择器的逻辑符号如下图：

数据选择器代码如下，可在本题答案中添加并例化此数据选择器。

module data_sel(
   input             S0     ,
   input             S1     ,
   input             D0     ,
   input             D1     ,
   input             D2     ,
   input             D3     ,
   
   output wire        Y    
);

assign Y = ~S1 & (~S0&D0 | S0&D1) | S1&(~S0&D2 | S0&D3);
     
endmodule

输入描述：

   input             A     ,
   input             B     ,
   input             C         

输出描述：

   output wire       L 

解题思路

4选1MUX相关知识

根据上述4选1MUX的示意图，得知：S0，S1为地址输入端，D0、D1、D2，D3为数据输入端，Y为数据输出端。下面给出4选1MUX的功能表：

S0	S1	Y
0	0	D0
1	0	D1
0	1	D2
1	1	D3

根据功能表，可以得出4选1MUX的逻辑函数式：

---

使用MUX实现逻辑函数

令变量A，B分别对应于S0，S1，则多余变量为C，余函数

则：

代码如下：

module sel_exp(
   input             A     ,
   input             B     ,
   input             C     ,
   
   output wire       L            
);

data_sel DS (.S0(A), .S1(B),
            .D0(1'b0), .D1(~C), .D2(C), .D3(1'b1),
            .Y(L));

endmodule