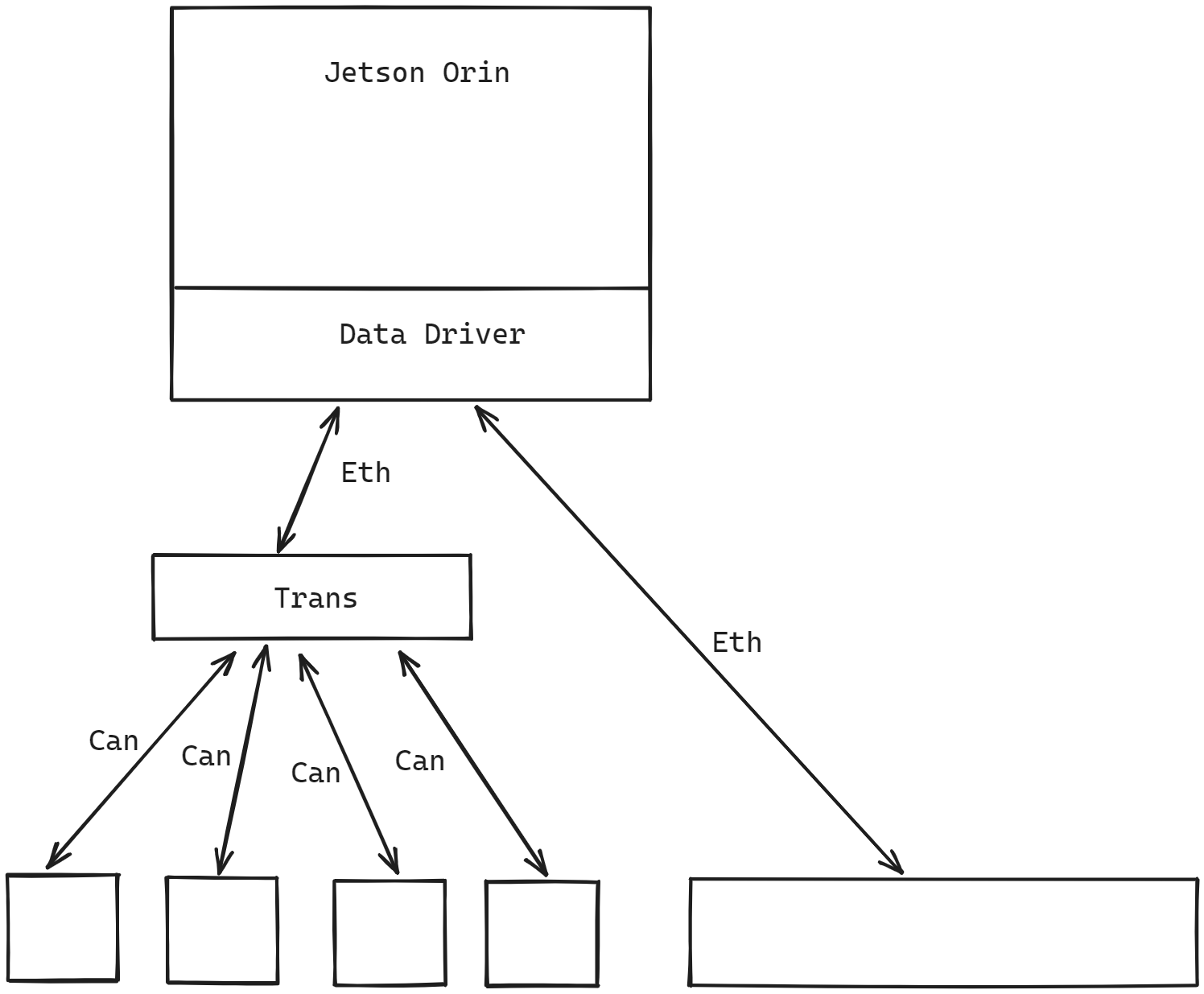
第一套
√
- 考点:基期比重差
- 很温柔的题
普通专科女生 占比 52.5% - 1.7% = 50.8%
成人本专科女生 占比 57.8% - 4.6% = 53.2%
相比降低了2.4%

×
- 知比重和部分量,求整体
- 在花生老师的解法中体会啥叫适当约分
0.1899 / 47.8% / 87.5%
==》0.19 / (49% * 7 / 8)
==》19 * 8 / (49 * 7)
==》19 / 42



√ - 考点:基期倍数
- 两个部分的数量比,转化为比重之比

√
可以用男童 = 整体- 女童,也可以求出整体基期和男童基期比重,得出男童基期
but花生老师强烈推荐第一种,因为能用两个减法解决的问题没必要用乘法。“女童超过2056万人”可以理解为2056.xx

×
①:“比重首次超过一半,达50.6%”,则之前是50%及以下,所以提高了0.6%+(对于50%的情况,花生老师认为一道题一般有一次弯,再多一次就太难了概率很低)
②:学会局部拆分
③:年均增长率 = (结束年份的增长率-开始年份的增长率)/(结束年份 - 开始年份)
④:这个10%是指多女生的10%

第二套
√
大致算出5000+即可,后续有5000+的需要进一步精度判断的再继续算即可

√
- 考点:增量贡献率 = 部分增量/整体增量
(联想:拉动增长 = 部分增量/ 整体前期 - 本题中的整体增量在题6中算过一次,直接用即可

√ - 考点:盐水的定性分析
- 可以把后两者视为一个整体,大概是10%,而剩下的公路工程3%,则肯定后两者都大于整体

√
原则上,先看没出现过的选项,但大前提是先看好算的选项,当没出现过但难算的选项就不再具有优先的必要啦

第三套
√
- 考点:平均类
- 观察选项差距较大,大致估算即可,现在还没有花生老师看出是多少的功力,可大致进行直除

√
类似于之前的“首次超过50%”的题,都是需要从给出的范围中进行推测
推荐用自己想出来的这种大致约算的方法,属于是难在逻辑,简单在数据型的题目

×
- 考点:增量数值比较
- 坑1:单位不同,统一单位才能比较(本题错误原因)
- 技巧:比较同一段时间内的平均增量,则等价于直接比较增量即可
- 起始时间:一方面问“14-18年”给出了13年,另一方面这是江苏题,无论哪个角度都应该往前推一年

√
- 考点:比重
- 题干省略:“四个地区的火力发电量占全国(火力)发电量”

×
①:

③:各有强项的乘积进行比较时
- 方法一(荐):可以把小的作为参考,看多出来的部分的大小比较,例如本题中分子1*1.1-,分母1.1+*1,则分母大
- 方法二:固定一个,比较另一个,例如本题中都是67份,则分子多出来626 * 5,分母多出来(720 - 626)* 67,则分母大

④:1/7 = 14.3%,2/7 = 28.6%

第四套
×
- 考点:求基期,保留三位进行假设分配
- 错误原因:找错主体,私人轿车找成了私人汽车

√ - 考点:比重
拆分

√


√
这题花生老师用比重法的话,还要算出来18年的整体量,也可以直接用男女比例

×
只知道各部分的增速,但不知道各部分的比重,则不能知道整体增速