• 定义：凸包是包围点云的最小凸多面体，所有点都在该多面体的内部或表面上。
• 优点：能够精确地包围点云，并且不存在额外的空白区域。
• 缺点：计算复杂度高，尤其是在高密度点云中，生成凸包的过程较慢。

下面，我将介绍两种常用的凸包算法的 Python 实现：

1. Graham 扫描算法
2. Andrew’s Monotone Chain 算法

生成测试数据

为了方便理解，我们现已二维数据进行测试

import numpy as np
mean = [0, 0]
cov = [[3, 1], [1, 2]]
points = np.random.multivariate_normal(mean, cov, 300)
plt.plot(points[:,0], points[:,1], 'o')

Graham 扫描算法

Graham 扫描算法的基本步骤如下：

1. 找到所有点中 y 坐标最小的点（如果有多个，则选择 x 坐标最小的）。
2. 将剩余的点按与起始点的极角进行排序。
3. 遍历排序后的点，使用栈维护当前的凸包顶点，判断转向方向以决定是否需要弹出栈顶点。

def graham_scan(points):
    # 找到 y 最小的点，若有多个则取 x 最小的
    start = min(points, key=lambda p: (p[1], p[0]))
    
    def polar_angle(p):
        return math.atan2(p[1] - start[1], p[0] - start[0])
    
    # 按极角排序，如果极角相同，离起点近的排前面
    sorted_points = sorted(points, key=lambda p: (polar_angle(p), (p[0] - start[0])**2 + (p[1] - start[1])**2))
    
    # 初始化栈
    stack = []
    for point in sorted_points:
        while len(stack) >= 2:
            o = stack[-2]
            a = stack[-1]
            b = point
            cross = (a[0] - o[0])*(b[1] - o[1]) - (a[1] - o[1])*(b[0] - o[0])
            if cross > 0:
                break
            stack.pop()
        stack.append(point)
    
    return stack
hull = np.array(graham_scan(points))
print("凸包顶点：", hull)
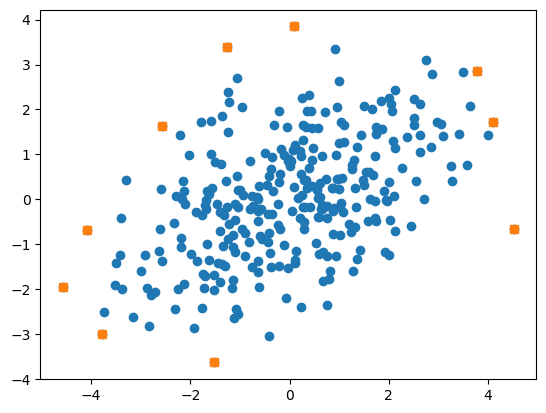
plt.plot(points[:,0], points[:,1], 'o')
plt.plot(hull[:,0], hull[:,1], 's')

代码解释：

1. 寻找起始点：使用 min 函数找到 y 坐标最小的点。如果存在多个点 y 坐标相同，则选择 x 坐标最小的。
2. 极角排序：根据每个点相对于起始点的极角进行排序。如果两个点的极角相同，则按照与起始点的距离从近到远排序。
3. 构建凸包：使用栈来维护当前的凸包顶点。对于每个点，检查它与栈顶两个点的转向方向。如果不是左转（即凸包的定义），则弹出栈顶点，直到满足凸包的条件。
4. 输出结果：最终栈中的点即为凸包的顶点。

输出结果:

凸包顶点： [[-1.51703261 -3.63377384] [ 4.51410791 -0.65295975] [ 4.10717132 1.7159215 ] [ 3.7692037 2.85400883] [ 0.08295138 3.84684229] [-1.25805766 3.39871686] [-2.56864639 1.63912747] [-4.09232528 -0.68889519] [-4.57389002 -1.96169353] [-3.7899005 -3.00607501]]

Andrew’s Monotone Chain 算法

Andrew’s Monotone Chain 算法是一种更高效的凸包算法，其时间复杂度为 O(n log n)。该算法首先将所有点按 x 坐标排序，然后分别构建下凸包和上凸包，最后合并两者。

def monotone_chain(points):
    # 确保输入是 NumPy 数组
    points = np.asarray(points)

    # 如果点集少于3个点，凸包即为所有点
    if len(points) <= 1:
        return points

    # 按 x 坐标排序，若 x 相同则按 y 坐标排序
    sorted_idx = np.lexsort((points[:,1], points[:,0]))
    sorted_points = points[sorted_idx]

    # 构建下凸包
    lower = []
    for p in sorted_points:
        while len(lower) >= 2:
            o, a = lower[-2], lower[-1]
            cross = (a[0] - o[0]) * (p[1] - o[1]) - (a[1] - o[1]) * (p[0] - o[0])
            if cross > 0:
                break
            lower.pop()
        lower.append(tuple(p))

    # 构建上凸包
    upper = []
    for p in reversed(sorted_points):
        while len(upper) >= 2:
            o, a = upper[-2], upper[-1]
            cross = (a[0] - o[0]) * (p[1] - o[1]) - (a[1] - o[1]) * (p[0] - o[0])
            if cross > 0:
                break
            upper.pop()
        upper.append(tuple(p))

    # 去除最后一个点（重复的起点）
    convex_hull = lower[:-1] + upper[:-1]

    # 转换为 NumPy 数组
    return np.array(convex_hull)


hull = monotone_chain(points)
print("凸包顶点：", hull)
plt.plot(points[:,0], points[:,1], 'o')
plt.plot(hull[:,0], hull[:,1], 's')

代码解释：

1. 排序：首先将所有点按 x 坐标排序，若 x 坐标相同则按 y 坐标排序。
2. 构建下凸包：
   • 遍历排序后的点。
   • 使用栈维护当前的下凸包顶点。
   • 对于每个新点，检查是否保持左转，如果不是，则弹出栈顶点。
3. 构建上凸包：
   • 遍历排序后的点的逆序（从右到左）。
   • 类似地，使用栈维护当前的上凸包顶点。
4. 合并结果：将下凸包和上凸包合并，注意去除重复的起点和终点。
5. 输出结果：最终的 convex_hull 列表即为凸包的顶点。
   输出结果

凸包顶点： [[-4.57389002 -1.96169353]
 [-3.7899005  -3.00607501]
 [-1.51703261 -3.63377384]
 [ 4.51410791 -0.65295975]
 [ 4.10717132  1.7159215 ]
 [ 3.7692037   2.85400883]
 [ 0.08295138  3.84684229]
 [-1.25805766  3.39871686]
 [-2.56864639  1.63912747]
 [-4.09232528 -0.68889519]]

Open3d实现代码

在三维点云处理中，我们在使用算法一般会利用别人高效实现的方式，这里使用open3d库实现凸包算法

import open3d as o3d
file_path = './data/5.txt'

point_cloud_data = np.loadtxt(file_path)

points = point_cloud_data[:, :3]
colors = point_cloud_data[:, 3:] / 255.0  # Open3D expects colors in [0, 1] range

pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)
pcd.colors = o3d.utility.Vector3dVector(colors)

hull, _ = pcd.compute_convex_hull()
hull_ls = o3d.geometry.LineSet.create_from_triangle_mesh(hull)
hull_ls.paint_uniform_color([1, 0, 0])  # 红色
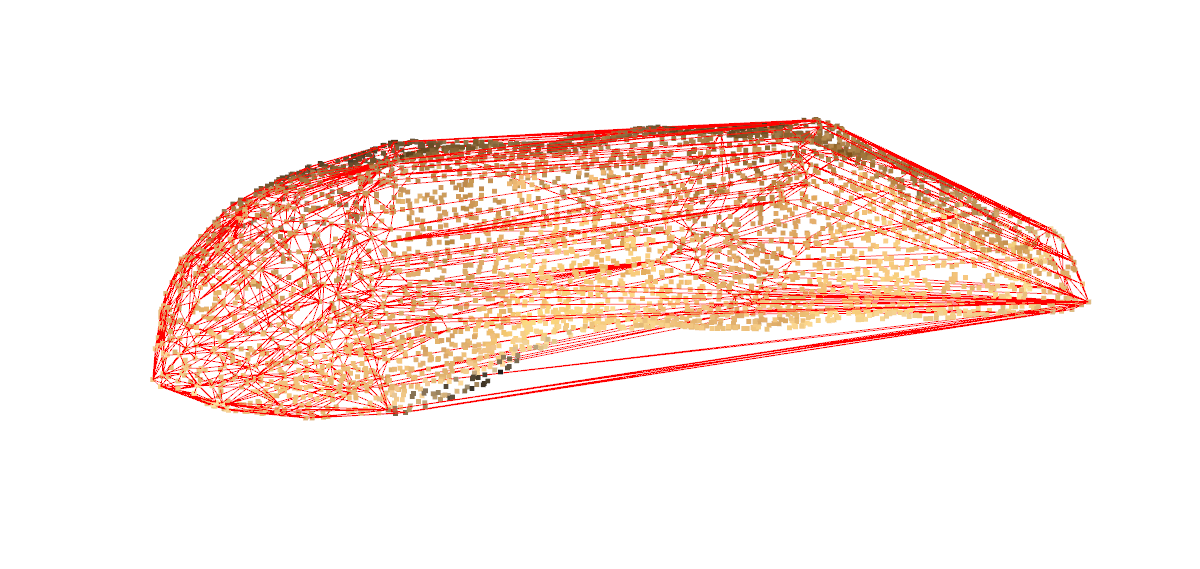
o3d.visualization.draw_geometries([pcd, hull_ls])

可视化结果：