【算法】最长公共子序列（C/C++）

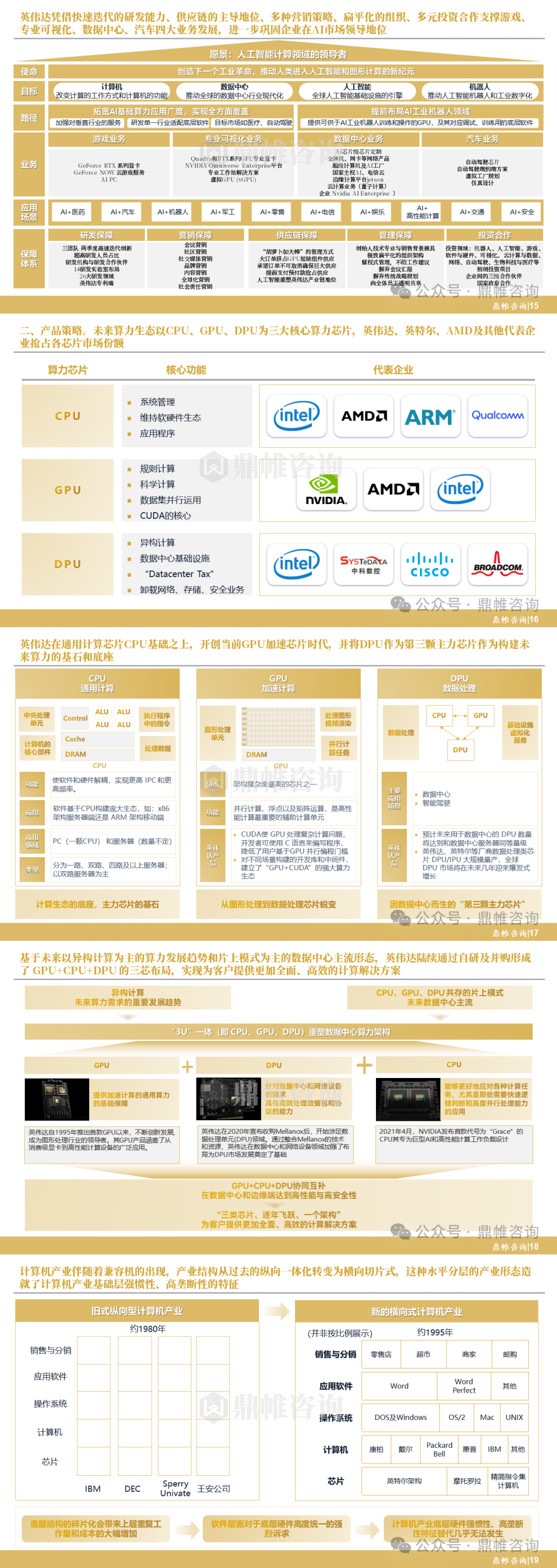
最长公共子序列（LCS，Longest Common Subsequence）问题简称（LCS），是动态规划里面里面的基础算法。它的所解决的问题是，在两个序列中找到一个序列，使得它既是第一个序列的子序列，也是第二个序列的子序列，并且该序列长度最长。由下图中两个序列，我们可以看出来最长公共子序列为[s c r g]。

我们来举个“栗子”，比如序列A为“abcdef”，序列B为“bcef”，那么它的最长公共子序列为序列B，即：“bcef”，注意最长公共子序列不用保证每一个字符必须连续。那么我们一般的暴力做法是什么呢？首先我们先要确定一个参照序列，这里以A为例吧，首先我们需要确定公共子序列的头部，由于选择了A序列为参照序列，那么遍历A序列的每一个字符，把这个遍历的字符与B序列的每一个字符相比较，若相等，A序列遍历到下一个字符，在B序列的基础上再与B序列的下一个字符为起点继续进行比较，直到序列结束，然后再确定A序列的下一个字符为头部，以此类推，从这里面找一个最大的数，即是最长公共子序列的长度。像这样做法，我们的时间复杂度也要O(n^2*m)（n为序列A的长度，m为序列B的长度）。这样的时间复杂度在做题时必然会WA掉，也是面试官不想看到的，我们肯定会有更为优秀的算法，下面我们介绍动态规划的思想。

动态规划：

上面我们说到每次确定公共子序列的头部时，我们的A序列需要重新返回来遍历A序列与B序列寻找相同的字符。这样的操作我们在第一次遍历时就已经遍历过一次，只是没有记录结果，如果我能够把这个结果记录下来，那么下一次再遍历到这个状态我们可以直接拿来用，避免了重复计算，大大减少了计算量，从而减少了时间复杂度。那么我们如何进行记录这个状态呢，我们设一个二维数组dp[i][j]，表示A序列的前i项与B序列的前j项所能构成的最长公共子序列长度。

dp[i][j]的状态转移方程分为两种，当A[i]==B[j]时dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);说明当时这两个字符相等，就等于A序列前一个字符跟B序列前一个字符这个状态+1。当A[i]！=B[j]时dp[i][j]=max(dp[i-1][j],dp[i][j-1]);若此时这两个字符不相等，那么就是A序列前一个字符跟B序列当前字符这个状态与B序列前一个字符跟A序列当前字符这个状态进行比较，哪一个大我当前dp[i][j]状态就从哪里转移。

 for(int i=1;i<=n;i++){
    for(int j=1;j<=m;j++)
     {
     	dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
     	if(A[i]==B[j])
     	dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
     }
 }

此时时间复杂度来到了O(n*m)（n为序列A的长度，m为序列B的长度），这样便可以解决大部分题目，有的题目还是解决不了的，对于更高级一点我们可以利用二分优化一下。时间复杂度便可以达到了O(nlog(n))，具体怎么实现下面我们讲解一下。

二分优化：

二分优化就是利用离散化操作，把两个数组通过映射为一个数组，在一个数组里面类似于求最长上升子序列操作，我们选择一个参照数组a，那么就要遍历数组b，考虑它的映射值大小与dp数组值得关系，其核心就一句口诀“大则添加，小则替换”。

解释一下什么意思。考虑新进来一个元素a[i]:

（1）大则添加：如果a[i]大于b[len]，直接让b[++len]=a[i]。即b数组的长度增加1，而且添加了一个元素。

（2）小则替换：如果a[i]小于或等于b[len]，就用a[i]替换掉b数组中第一个大于或等于a[i]的元素。

假设第一个大于a[i]的元素是b[j],那么用a[i]换掉b[j]后，会使得b[1...j]这个上升子序列的结尾元素更小。对于一个上升子序列，其结尾元素越小，越有利于续接其它元素，也就越可能变得更长，也就是说替换完使序列更有潜力，更容易接纳元素。

int a[105]={1,6,3,2,7,4,3,3,2};
int b[105];
int m=9;
int len=1;
b[1]=a[1];
int find(int x){//二分查找
	int L=1,R=len,mid;
	while(L<=R){
		mid=(l+r)>>1;
		if(x>b[mid])L=mid+1;
		else R=mid-1;
	}
	return L;
}

for(int i=2;i<=n;i++){
	if(a[i]>b[len]){//大则添加
		b[++len]=a[i];
	}else{//小则替换
		j=find(a[i]);
		b[j]=a[i];
	}
}
printf("%d\n",len);

图解算法：

文字去描述二分优化的过程不太好描述跟理解，那么我们进行图解一下算法的实现过程，希望对大家有所帮助。

我们以数组A=[3,1,4,2]，数组B为[2,1,3,4]为例，进行图解。

初始化：离散化操作，对数组A进行离散化处理，得到map映射数组，拿着这个映射数组去把B数组的映射数组求出来。

第一步：预处理部分做完了就要开始我们的真正的实现了。当前我们初始化了dp数组为无穷大，由于我们选取了数组A为参照数组，那么我们就去遍历数组B的映射数组，这里就用到了我们所说的口诀“大则添加，小则替换”，此时数组B的映射数组第一个为4，dp数组里面都是inf，4<inf，小则替换，我们就去dp数组里面寻找第一个大于等于4的位置，给它替换成4，很明显dp数组第一个位置（下标为0）由inf替换成4。

第二步：数组B的映射数组到了第二个数了（下标为1），dp里面此时有一个数了，当前遍历的数为2，2与当前dp位置上的数比较，2<4，小则替换，很明显把dp第一个位置上的数4替换成2。

第三步：此时遍历到第三个数（下标为2），当前数组B的映射数组的值为1，1与当前dp数组上的位置相比较，1<2，小则替换，则把2替换为1。

第四步：此时遍历到最后一个位置了，当前数组B的映射数组的值为3，3与dp数组上当前位置上的数进行比较，3>1，根据口诀大则添加，则把3加到当前dp位置后面，即把dp[1]=3。

最终dp的长度为2，那么最长公共子序列的长度的值为2。由此dp数组我们还可以得到最长公共子序列是哪一个序列，这样我们反推回去，当前dp[0]=1,dp[1]=3，1对应的映射为3，3对应的映射为4，那么我们所得到的最长公共子序列就是[3，4]。

原题链接：【模板】最长公共子序列 - 洛谷

题目描述

给出 1,2,…,n 的两个排列P1 和 P2 ，求它们的最长公共子序列。

输入格式

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…,n 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

输入

5 
3 2 1 4 5
1 2 3 4 5

输出

说明/提示

对于 50%的数据， n≤10^3；

对于 100%的数据，n≤10^5。

解题思路：

最长公共子序列有两种解法，分别是朴素解法和一种二分优化的解法，此题10^5，若用第一种朴素解法肯定会TLE，所以下面我们详细介绍第二种解法。

朴素解法（会TLE）

很明显我们去枚举序列1的每一位和序列2的每一位，如果两个数字相等，那么dp[i][j]=dp[i-1[j-1]+1。最后计算dp[n][n]即可。

代码实现：

#include<iostream>
using namespace std;
const int N=1005;
int dp[N][N],a1[N],a2[N],n;
int main()
{
   //dp[i][j]表示两个串从头开始，直到第一个串的第i位 
   //和第二个串的第j位最多有多少个公共子元素 
   cin>>n;
   for(int i=1;i<=n;i++)cin>>a1[i];
   for(int i=1;i<=n;i++)cin>>a2[i];
   for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
     {
     	dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
     	if(a1[i]==a2[j])
     	dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
     	//因为更新，所以++； 
     }
   cout<<dp[n][n]<<endl;;
   return 0;
}

优化解法

主要跟最长上升子序列的优化方法一样的，记住这句话就可以，“大则添加，小则替换”，这就是实现的思路，当此时要进入的值大于最长子序列的最后值就添加，若小于最长子序列的最后的值，则找到最长子序列中第一个大于此值的下标把它给替换掉。

代码实现：

#include<iostream>
using namespace std;
const int N=1e5+5;
int n,len=1;
int a[N],b[N],dp[N],map[N];//mapA映射B，相当于A数组当标准，操作B数组，压缩为一个数组，
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i],map[a[i]]=i;//map映射
	for(int i=1;i<=n;i++)cin>>b[i],dp[i]=0x3f3f3f;//初始无穷大
	for(int i=1;i<=n;i++){
		if(map[b[i]]>dp[len])dp[++len]=map[b[i]];//大则添加
		else dp[lower_bound(dp,dp+len,map[b[i]])-dp]=map[b[i]];//小的替换，lower_bound实现更简单
	}
	cout<<len<<endl;//最后输出长度即可
	return 0;
}

最长公共子序列（LCS）是算法动态规划之中最基础的部分，是每一位算法初学者的首选，也是数学之中必学的内容，文章尚有不足，若有错误的地方恳请各位大佬指出。

执笔至此，感触彼多，全文将至，落笔为终，感谢大家的支持。