【测向定位】差频MUSIC算法DOA估计【附MATLAB代码】

news2024/11/15 9:19:36

微信公众号：EW Frontier QQ交流群：554073254

摘要

利用多频处理方法，在不产生空间混叠的情况下，估计出高频区域平面波的波达方向。该方法利用了差频（DF），即两个高频之间的差。这使得能够在可行区域中处理数据而没有空间混叠。分析了测向处理中的DOA特性，提出了一种基于MUSIC的多测向多快拍处理方法。本文提出了一种将多个DF和多个快拍联合考虑的方法，以及一种联合DF方法，该方法提供了一个不需要固定DOA的单快拍DF-MUSIC。仿真算例证明了文章提出方法的有效性并讨论了其DOA性能。

引言

由于空间混叠，均匀线阵将平面波DOA估计限制在一个较高的频率范围内。为了考虑数据的特定频率分量，应该在每个波长两个以上的点处对数据进行采样。否则，波达方向变得不明确，组件在错误的波达方向。当处理更高频率的带外信号时，无源系统尤其会出现这个问题。

我们解决了高频DOA估计，并采用多频处理。来自宽带信号中的多个频率的更多数据实现处理增益并获得良好的估计[1]，[2]，[3]，[4]。为了更好地进行宽带DOA估计，已经提出了稀疏信号重构[5]，[6]，[7]，[8]，[9]，[10]。基于循环平稳性的宽带方法是另一种技术，并且利用时间和空间中的循环相关特性[11]，[12]，[13]，[14]，[15]。利用多频点的频谱特性，对著名的非均匀线阵--互素阵的DOA估计进行了改进[16]，[17]，[18]，[19]。

多频处理利用差频（DF），即频率f处的阵列数据与另一个f +Δf处的复共轭的乘积，这使得能够处理在没有空间混叠的情况下，使用较低频率Δf区域中的数据[20]，[21]。远场源的DOA估计具有平面波和的阵列数据模型。

DF技术已应用于源定位和DOA估计，并通过实验数据进行了验证[21]，[22]，[23]，[24]。对于源定位，已应用匹配场处理，其使用波传播模型匹配测量和模拟信号[25]，[26]，[27]，[28]。对于DOA估计，使用常规波束形成器（CBF）或延迟求和波束形成器[21]。使用高频的DF方法显示出与低频CBF相当的DOA性能[22]。通过反卷积[23]以及通过使用MVDR和进一步的分析考虑[24]来改进基于DF的CBF的DOA性能。如图所示，DF处理使用频率f处的阵列数据和f +Δf处的复共轭数据的Hadamard乘积。

本文提出了三种联合收割机组合多个时间和测向样本的方法：时间、频率和时频联合。时间-DF-MUSIC对单个DF使用多个时间样本以获得时间平均样本协方差矩阵（SCM）。利用DF会产生不需要的伪影DOA [21]、[22]、[24]，其取决于真实DOA和DF频率。由于伪影DOA在DF上变化，因此单独获得每个DF的MUSIC频谱并在频率上求平均可减轻伪影。

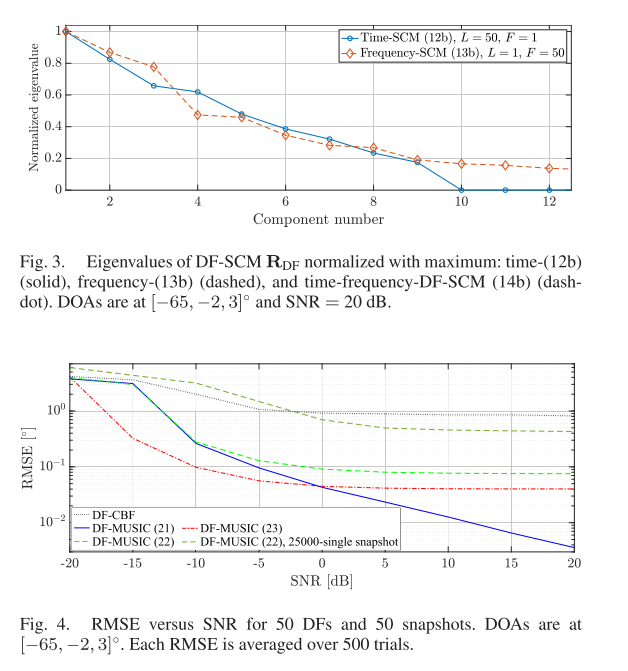
频率-DF-MUSIC使用均匀间隔的多个DF，具有相同的DF以获得频率平均的SCM。对于真实DOA，恒定DF共享相同的导向矢量，并且多DF等效于多快照。频率处理采用多个DF，实现了单次快拍DOA估计。单次时间快拍方法对于时变波达方向是有用的。

时频DF-MUSIC联合收割机将所有时间和DF样本合并到SCM中。该方法利用更多的数据平均来改善DOA估计。

文章插图

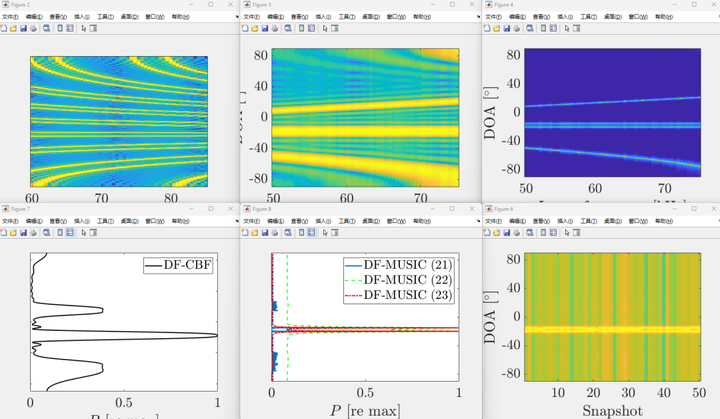
结论

推导了一种对多个频率的高频源及其差频进行DOA估计的算法，以获得低频处理。由于DF低于混叠频率，因此这是无空间混叠的。时间-DF-MUSIC算法将时间样本合并到样本协方差矩阵中，得到每个DF处的MUSIC谱，并对谱进行平均以估计最终DOA。频率-DF-MUSIC适用于单次快照，并且不需要随时间的固定DOA。时频-DF-MUSIC算法综合了所有的时频信息，联合使用更多的数据量获得处理增益。

MATLAB代码展示

%%
clear; clc;
close all;

% addpath([cd,'/_common'])
% addpath(['../_common'])
errCut = 10; % Maximum RMSE cut-off.

% rngNumber = 1; rng(rngNumber);
dbstop if error;

run_bpdn = 0;

%%
% Environment parameters
% c = 1500;       % speed of sound
c = 343;       % speed of sound

dfreq = 10000;                % difference frequency [Hz]

% ULA-horizontal array configuration
d = .5*(c/dfreq);            % intersensor spacing (based on DF)
% d = 3.75;                  % intersensor spacing [m]
% f = 200; % Hz -> 0.5 lambda = 0.5 * 1500 / 200 = 3.75 [m]

Nsensor = 20;               % number of sensors
q = (0:1:(Nsensor-1))';     % sensor numbering
xq = (q-(Nsensor-1)/2)*d;   % sensor locations

% 5-7.5 times to Difference Frequency (DF)
fmul1 = 5;
fmul2 = 7.5;
ftmp = linspace(fmul1*dfreq,fmul2*dfreq,50);
f = [ftmp,ftmp+dfreq];      % frequency [Hz]
Nfreq = numel(f);

lambda = c./f;   % wavelength


% signal generation parameters
SNR = 20;

% total number of snapshots
Nsnapshot = 50;

% range of angle space
thetalim = [-90 90];

theta_separation = .005;

% Angular search grid
theta = (thetalim(1):theta_separation:thetalim(2))';
Ntheta = length(theta);

% Generate received signal
anglesTrue = [-40; 35];
fprintf(['True DOAs        :',...
    repmat([' %.4f '],1,numel(anglesTrue)),'\n'],anglesTrue.')