1734. 解码异或后的排列

news2024/11/15 12:05:01

1. 题目

1734. 解码异或后的排列

2. 解题思路

要搞明白这个题目可以先来看下它的简化版题目：1720. 解码异或后的数组

[!NOTE] 题目：
未知整数数组 arr 由 n 个非负整数组成。
经编码后变为长度为 n - 1 的另一个整数数组 encoded ，其中 encoded[i] = arr[i] XOR arr[i + 1] 。例如，arr = [1,0,2,1] 经编码后得到 encoded = [1,2,3] 。
给你编码后的数组 encoded 和原数组 arr 的第一个元素 first（arr[0]）。
请解码返回原数组 arr 。可以证明答案存在并且是唯一的。

异或操作：两个二进制数字进行异或(^)操作的时候，相同为0不同为1

假设元素z来自于encoded中，是编码之后的内容，x和y源于arr，且二者相邻。根据题目设定，显然有：x XOR y = z的关系。
那我们看看异或运算的真值表：
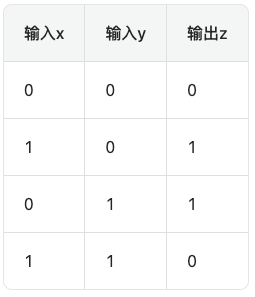
image.png|400
现在只知道后面两列输入y和输出z，将这两个元素当成“输入”，那么原本的输入x就是“输出”：

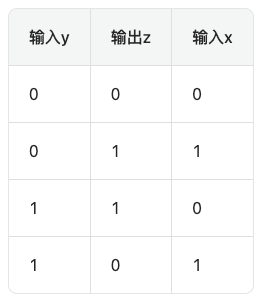
总结上表规律，就是x = y XOR z。
简单小结上面内容，就是：

if x XOR y = z
then x = y XOR z

这个就是解决本题的核心。
另附带1720. 解码异或后的数组的解题代码

class Solution {
    public int[] decode(int[] encoded, int first) {
        int n = encoded.length;
        int[] perm = new int[n + 1];
        perm[0] = first;
        for (int i = 1; i < perm.length; i++) {
            perm[i] = perm[i - 1] ^ encoded[i - 1];
        }
        return perm;
    }
}

[!important] 我们再来看下本题的重点：
整数数组 perm ，它是前 n 个正整数的排列，且 n 是个奇数
这代表了什么呢？
排列就是n个自然数，从1到n随机排序。比如n=5，就是1到5这五个数的随机排列

我们抽象一下1720. 解码异或后的数组的思路，其实就是知道perm中的两个数，就能异或出encode中对应的数。本题与1720. 解码异或后的数组相差的就是不知道perm中的第一个数字，那我们只需要求出perm中的第一个数，剩下的就好办了。
我们可以用int ABCDE 来代表perm所有数字异或的结果。int BCDE 代表除了perm中第一个元素以外所有元素异或的值。
注意：AB=A^B 后面简写了！！！

既然我们知道了perm = [A, B, C, D, E]，那么encoded = [AB, BC, CD, DE]；
根据perm，我们可以得到ABCDE,根据encoded的BC和DE，我们可以得到BCDE；
将ABCDE和BCDE进行异或运算，得到A，即perm的第一个元素。

然后就可以推导剩余的元素了。

3. 代码

3.1. 注意点

[!NOTE] 1、为什么ABCD = ABCD ^ i ？且for循环能到encoded.length+1
首先题目说的perm它是前 n 个正整数的排列,且是奇数，那么我们求它的所有值的异或，就遍历1到N进行异或就行。
这里的N就是encoded.length+1，比如perm=[1,2,3] 那encode=[1^2,2^3] 长度总比perm少1

[!NOTE] 2、BCD的值怎么求的
首先看循环截止，它是遍历了encode的所有值，而且i是从1开始的。我们来看个例子

我们要相当于要求bcde的异或结果，那其实等价于encode[1]、encode[3]异或的结果。这也是为什么循环中每次i=i+2而不是i++ ，每次跳过一个数字就能达到目的。

[!NOTE] 3、为什么perm[0] = ABCD ^ BCD
如果 A、B、C、D 都是单独的数字，并且 ABCD 和 BCD 是这四个数字的异或操作，那么我们可以这样表示：

ABCD = A ^ B ^ C ^ D
BCD = B ^ C ^ D

异或运算的特性是：若 x^x=0 和 x^0=x，所以
A = (A ^ B ^ C ^ D) ^ (B ^ C ^ D)
这样，A 的值将被保留下来，而 B、C 和 D 将抵消。
注意，异或操作是在二进制数字的前提下！

3.2. 完整代码

class Solution {
    public int[] decode(int[] encoded) {
        int n = encoded.length;
        //整个perm数组进行异或运算后的值，比如：[1,2,3,4] 那ABCD就代表1^2^3^4
        int ABCD = 0;

        //由于perm它是前 n 个正整数的排列[排列就是n个自然数，从1到n随机排序。比如n=5，就是1到5这五个数的随机排列。]，且 n 是奇数。所以perm的长度为n+1
        //例如perm=[1,0,2,1]那么encode=[1(1^0),2(0^2),3(2^1)]
        for (int i = 1; i <= n + 1; i++) {
            ABCD = ABCD ^ i;
        }

        //除了perm中第一个元素以外所有元素异或的值
        int BCD = 0;
        //遍历encode
        for (int i = 1; i < n; i = i + 2) {
            BCD = BCD ^ encoded[i];
        }
        int[] perm = new int[n + 1];
        perm[0] = ABCD ^ BCD;
        for (int i = 1; i < perm.length; i++) {
            perm[i] = perm[i - 1] ^ encoded[i - 1];
        }
        return perm;
    }
}