本案例发生在新人的PCB设计文件中，当然就算硬件老人们，其实只要不注意也很容易出现这种全局网络乱用的问题。

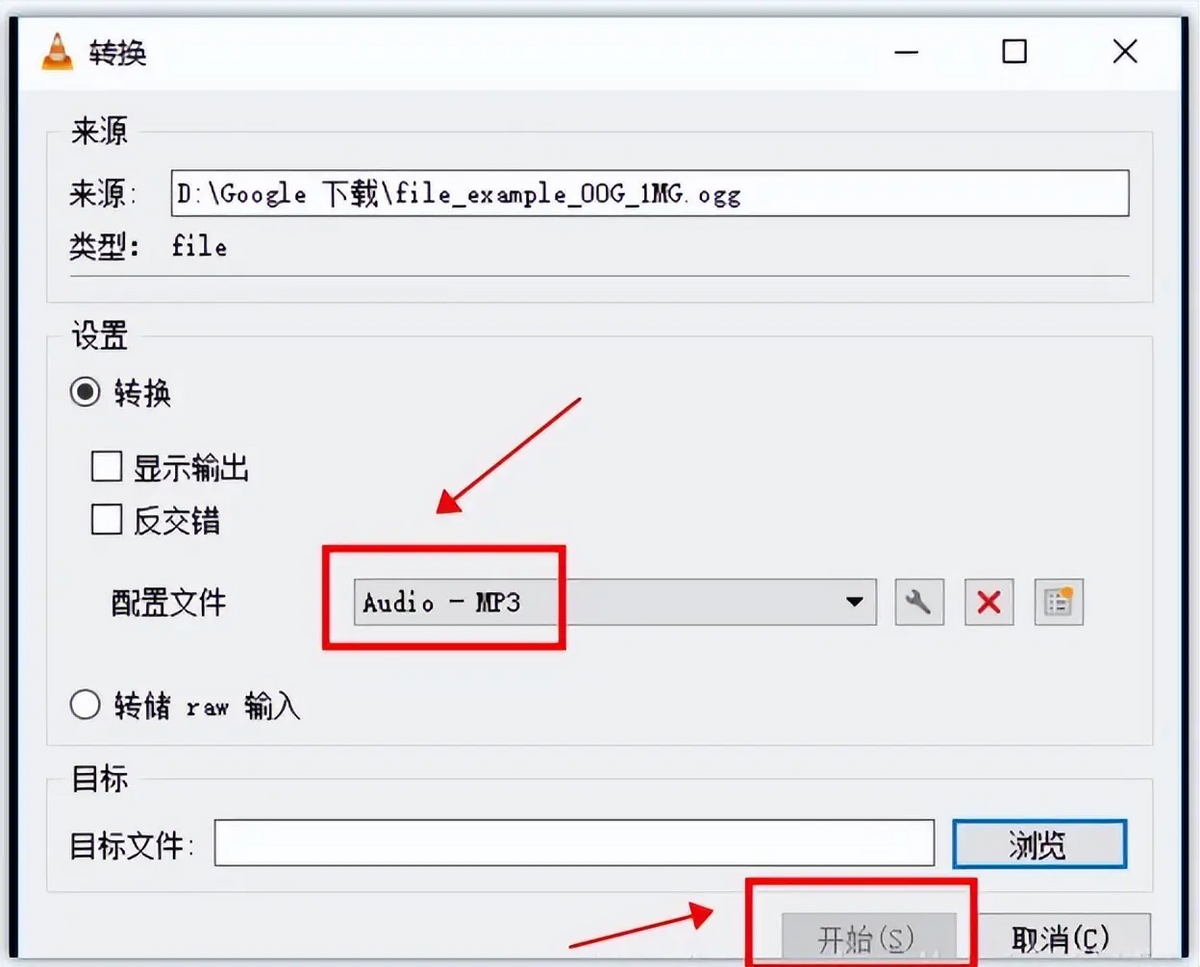
        如下所示是给新人的接口参考图纸，要求使用嘉立创绘制16个相同的接口做一个工装板。同时还要增加单片机实现切换控制功能。可以看到座子的24个管脚中使用到了3.3V、GND、LED、VCC、RST、IO、C8、C4、CLK等信号。

        结果新人上交的作业中，同样是一个座子，但看到3.3V电源被更换成了3V电源。 询问他抄图纸抄着抄到哪里去，电源网络也能抄错？设计DRC有没有检查等信息。得到的回复是DRC有检查，没有报错，但现在被指出来有问题，才发现确实电源网络不同，是自己画错了。

       查看在工程设计的网络，不同的电源和数量关系，其中主要电源有V3.0、V3.3、V5.0。