原文链接：使用梯度下降法实现多项式回归 - 柒墨轩 - 博客园

使用梯度下降法实现多项式回归

实验目的

本实验旨在通过梯度下降法实现多项式回归，探究不同阶数的多项式模型对同一组数据的拟合效果，并分析样本数量对模型拟合结果的影响。

实验材料与方法

数据准备

1. 生成训练样本：我们首先生成了20个训练样本，其中自变量X服从均值为0，方差为1的标准正态分布。因变量Y由下述多项式关系加上均值为0，方差为1的误差项er​构成： Y=5+4X+3X2+2X3+er​​
2. 数据可视化：使用Matplotlib库绘制了生成的数据点。

代码

import numpy as np
import matplotlib.pyplot as plt

# 设置随机种子以保证实验可重复性
np.random.seed(0)

# 生成20个训练样本
n_samples = 20
X = np.random.normal(0, 1, n_samples)
e_r = np.random.normal(0, 1, n_samples)  # 误差项

# 计算Y值
Y = 5 + 4 * X + 3 * X**2 + 2 * X**3 + e_r

# 使用matplotlib显示生成的数据
plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color='blue', label='Actual data')
plt.title('Generated Data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()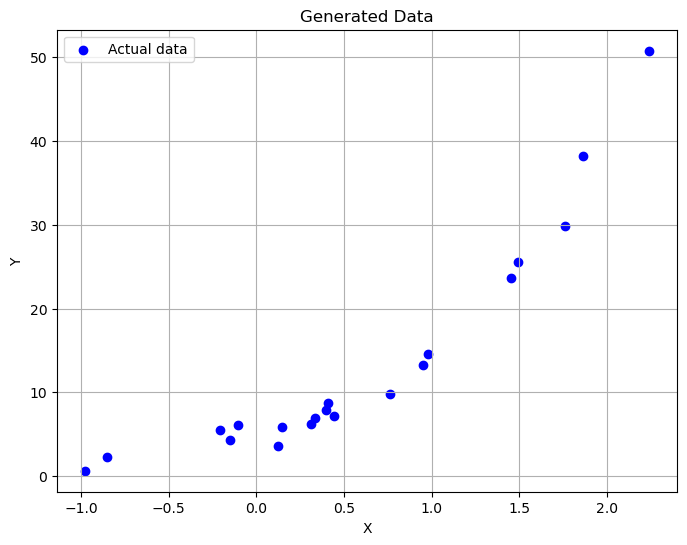

模型定义

1. 定义多项式回归模型：我们定义了一个MultinomialModel类，该类接受训练数据作为输入，并能够返回多项式模型的参数。类内部包括构造设计矩阵的方法、拟合数据的方法（使用梯度下降法）以及预测方法。

代码

class MultinomialModel:
    def __init__(self, degree):
        self.degree = degree
        self.coefficients = None
    
    def _design_matrix(self, X):
        """构造设计矩阵"""
        n_samples = len(X)
        design_matrix = np.ones((n_samples, self.degree + 1))
        for i in range(1, self.degree + 1):
            design_matrix[:, i] = X ** i
        return design_matrix
    
    def fit(self, X, Y, learning_rate=0.01, iterations=1000):
        """使用梯度下降法来拟合模型"""
        n_samples = len(X)
        self.coefficients = np.zeros(self.degree + 1)  # 初始化系数
        
        # 构造设计矩阵
        X_design = self._design_matrix(X)
        
        for _ in range(iterations):
            # 预测
            predictions = np.dot(X_design, self.coefficients)
            
            # 损失函数的导数
            gradient = 2 / n_samples * np.dot(X_design.T, predictions - Y)
            
            # 更新系数
            self.coefficients -= lea