基础算法（3）—

1. 二分查找

题目描述：

解法一：暴力解法（时间复杂度 $O(N)$ )

循环遍历数组，找到相等的值返回下标即可

解法二：二分查找

“有序数组可使用二分查找”，这句话是不严谨的，应该是具有 “二段性” 的数组都可以使用二分查找

细节：

1) 循环结束的条件：left > right，因为 [left, right] 中的元素都是未知的，并没有判断是否满足条件，因此当 left == right 时，也许判断

2) 二分查找的正确性：因为在本题中，数组是有序的，如：nums = [-1,0,3,5,9,12], target = 9，当取到值 5 时，小于 9，因为数组有序，所有 5 前面的值相当于已经判断过了，肯定小于 9，一步做完了暴力枚举的很多工作，因为暴力枚举可以完成本题，所以二分查找是可以正确解决问题的

3) 时间复杂度：

当暴力枚举时间复杂度为 2 的 32 次方时，二分查找只需要查找 32 次，时间复杂度比暴力枚举小非常多

代码实现：

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        //初始化 left 和 right 指针
        int left = 0;
        int right = n - 1;
        //由于两个指针相交时，当前元素还未判断，因此判断条件需要取等号
        while (left <= right) {
            //先找到中间元素
            //int mid = (left + right)/2; //该种写法有溢出风险（如：若数组长度为2的32次方，相加的话有可能会超出 int 类型能存储的极限
            int mid = left + (right - left) / 2; //让 left + 整个数组的一半长度来取中间值，肯定不会溢出
            //分三种情况讨论
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

tip：计算中间值时，使用 (left + right) / 2，这种写法有溢出风险，如：若数组长度为 2 的 32 次方，相加的话有可能会超出 int 类型能存储的极限

总结朴素二分查找模板：

while (left <= right) {
    int mid = left + (right - left) / 2; //数组长度为偶数时，该种写法会取到数组中间靠左的元素
    //int mid = left + (right - left + 1) / 2; //这两种写法都能完成任务，只是当数组长度为偶数时会有所差别，该种写法会取到数组中间靠右的元素

    if (...)
        left = mid + 1;
    else if (...)
        right = mid - 1;
    else
        return ...;
}

2. 在排序数组中查找元素的第一个和最后一个位置

题目描述：

解法一：暴力查找（时间复杂度 $O(N)$ ）

遍历数组找到目标值在数组中的开始和结束位置即可

解法二：二分

朴素二分代码实现：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int n = nums.length;
        int left = 0;
        int right = n - 1;
        int[] arr = {-1, -1};

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] >  target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                left = mid - 1;
                right = mid + 1;
                while (left >= 0 && nums[left] == target) {
                    left--;
                }
                while (right < n && nums[right] == target) {
                    right++;
                }
                arr[0] = left + 1;
                arr[1] = right - 1;
                return arr;
            }
        }
        return arr;
    }
}

朴素二分在极端情况下，如：数组全是 3，要查找 3 时，时间复杂度和暴力查找是一样的，都是 $O(N)$

优化：根据数组的“二段性”，分别二分查找其左右端点

算法思路：

第一步：查找区间的左端点

可分为两种情况：
1. x < t：left = mid + 1（当 x 小于 t 时，左侧的值肯定都小于 t，所以 left 可以直接跳到 mid 的下一个位置）

2. x >= t：right = mid
（因为这一步是查找区间的左端点，所以把大于和等于放一起，当 x = t 时，像本例中，不一定是哪一个 3，若正好是左端点的 3，此时 right = mid - 1 的话，就把左端点错过了）

细节处理：

1) 循环条件必须设置为 left < right，因为 left = right 时就是最终结果，无需判断

2) 求中点的操作

mid 必须为：left + (right - left) / 2，否则死循环

第二步：查找区间右端点

可分为两种情况：
1. x <= t：left = mid

因为此步骤是为求右端点，因此右端点以前的 target 不重要，所以将小于和等于这两个判断条件放到一起，只是为了避免出现当前下标处就是右端点时，操作 left = mid + 1 错过右端点

2. x > t：right = mid - 1

当 x 大于 t 时，右侧的值肯定都大于 t，因此 right 可以直接跳到 mid 的前一个位置

细节处理：

1) 循环条件必须设为 left < right，原因同上

2) 求中点的方式

mid 必须为：left + (right - left + 1) / 2，否则死循环

代码实现：

//根据数组的 “二段性”，分别二分查找其左右端点
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] arr = {-1, -1};
        if (nums.length == 0) { //处理边界
            return arr;
        }
        //二分左端点
        int left = 0;
        int right = nums.length - 1;
        while (left < right) { //细节1：此处判断条件不能是小于等于，否则死循环
            //细节2：此处不能用 left + (right - left + 1) / 2，否则死循环
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) { //细节3：区分二分左端点和右端点此处的条件
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        //循环结束后，left == right
        //判断一下当前下标处是否为 target，若不是则该数组中不存在目标值
        if (nums[left] != target) {
            return arr;
        }
        //若当前下标处等于 target，则此下标即为目标值在数组中的开始位置
        arr[0] = left;

        //二分右端点，已经找到左端点了，left 没必要从 0 开始了，只需将 right 重置即可
        right = nums.length - 1;
        while (left < right) {
            //细节4：此处不能用 left + (right - left) / 2，否则死循环
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] <= target) { //细节5：同细节3
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        //循环结束后，left == right，此时下标即为目标值在数组中的结束位置
        arr[1] = right;
        return arr;
    }
}

总结二分模板

3. 搜索插入位置

题目描述：

解法：二分查找算法

算法思路：

代码实现：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0;
        int right = n - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            //将数组分为两个区间
            //第一个区间都是小于 target 的，当 left 下标处值小于 target 时，left = mid + 1
            if (nums[mid] < target) {
                left = mid + 1;
            } else { //第二个区间是大于等于 target 的，当 righ 下标处值大于等于 target 时，right = mid
                right = mid;
            }
        }
        if (nums[right] < target) { //当循环结束，没有找到目标值，说明需要在数组末尾插入
            return right + 1;
        }
        return right;
    }
}

4. x 的平方根

题目描述：

解法一：暴力枚举

算法思路：

代码实现：

//暴力枚举
class Solution {
    public int mySqrt(int x) {
        //为避免两个较大的数超出 int 的范围，此处定义为 long 类型
        for (long i = 0; i <= x; i++) {
            if (i * i > x) { //如果两个数相乘大于 x，返回 i - 1
                return (int)i - 1;
            } else if (i * i == x) { //如果两个数相乘等于 x，返回 i
                return (int)i;
            }
        }
        return -1;
    }
}

解法二：二分查找

算法思路：

代码实现：

//二分查找
class Solution {
    public int mySqrt(int x) {
        //当 x 小于 1 时，直接返回 0
        if (x < 1) {
            return 0;
        }
        long left = 1; //left 从 1 开始，且需用 long 类型
        long right = x;
        while (left < right) {
            long mid = left + (right - left + 1) / 2; //下面会涉及到 *，所以使用 long 类型防溢出
            if (mid * mid <= x) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return (int)left;
    }
}

5. 山峰数组的峰顶索引

题目描述：

解法一：暴力枚举

代码实现：

//暴力枚举
class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int max = -1;
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > arr[i-1]) {
                max = i;
            }
        }
        return max;
    }
}

解法二：二分查找

算法思路：

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int n = arr.length;
        int left = 1; //题目规定第一个位置和最后一个位置绝无可能满足要求，因此可跳过
        int right = n - 2;
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (arr[mid] > arr[mid - 1]) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }
}

6. 寻找峰值

题目描述：

解法一：暴力枚举

算法思路：

//暴力枚举
class Solution {
    public int findPeakElement(int[] nums) {
        int max = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] > nums[max]) {
                max = i;
            }
        }
        return max;
    }
}

解法二：二分查找

算法思路：

代码实现：

//二分查找
class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        int left = 0;
        int right = n - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[mid + 1]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

7. 寻找旋转排序数组中的最小值

题目描述：

解法一：暴力枚举（时间复杂度 $O(N)$ ）

代码实现：

//暴力枚举
class Solution {
    public int findMin(int[] nums) {
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] < min) {
                min = nums[i];
            }
        }
        return min;
    }
}

解法二：二分查找

题目中的数组规则如下图所示：

上图中 C 点就是我们要求的点

二分的本质：找到一个判断标准，使得查找区间能够一分为二

通过图像我们可以发现，[A, B] 区间内的点都是严格大于 D 点值的，C 点的值是严格小于 D 点值的，但是当 [C, D] 区间只有一个元素的时候，C 点的值是可能等于 D 点值的

因此，初始化左右两个指针 left、right，

然后根据 mid 的落点，可以如下划分下一次查询的区间：

当 mid 在 [A, B] 区间的时候，也就是 mid 位置的值严格大于 D 点的值，下一次查询区间在 [mid + 1, right] 上

当 mid 在 [C, D] 区间的时候，也就是 mid 位置的值严格小于等于 D 点的值，下次查询区间在 [left, mid] 上

当区间长度变为 1 的时候，就是要查询的结果

代码实现：

class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int left = 0;
        int right = n - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[n - 1]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return nums[left];
    }
}

以 A 点为参照物的解法

上面解法是以 D 点当作参照物，若是以 A 点当作参照物的话，需要考虑一种特殊情况：

nums = [0,1,2,4,5,6,7] 若是旋转 7 次
依旧得到 nums = [0,1,2,4,5,6,7]
此时 A 点的值严格小于 D 点

如果是上面的特殊情况，若是以 A 点作为参照物的话，会出现错误答案

将特殊情况特殊处理即可

代码实现：

class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int left = 0;
        int right = n - 1;
        //特判
        if (nums[0] < nums[n - 1]) {
            return nums[0];
        }
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < nums[0]) {
                right = mid;
            } else { //元素值 互不相同 的数组,没有相等的情况
                left = mid + 1;
            }
        }
        return nums[left];
    }
}

8. 点名

题目描述：

解法一：暴力枚举

//暴力枚举
class Solution {
    public int takeAttendance(int[] records) {
        int n = records.length;
        int i = 0;
        for (; i < n; i++) { //遍历数组
            if (records[i] != i) { //若当前下标处值与下标不同，此时下标值即为缺席同学学号
                return i;
            }
        }
        //题目说明，肯定有一个同学缺席
        //若循环结束仍未返回，则缺席同学学号为最后一位，也就是当前 i 的值
        return i;
    }
}

解法二：哈希表

//哈希表
class Solution {
    public int takeAttendance(int[] records) {
        int n = records.length;
        int[] hash = new int[n + 1]; //创建一个 n + 1 大小的数组模拟哈希表
        for (int i = 0; i < n; i++) { //遍历 records，使其中元素作为下标，让 hash 中对应下标处值 ++
            hash[records[i]]++;
        }
        int j = 0;
        for (; j < hash.length; j++) { //循环遍历 hash，其中值为 0 的下标即为缺席同学学号
            if (hash[j] == 0) {
                return j;
            }
        }
        //若判断条件为 j < hash.length，代码不会走到这
        //若判断条件为 j < n，代码可能会走到这
        return j;
    }
}

解法三：位运算

//异或运算
class Solution {
    public int takeAttendance(int[] records) {
        int n = records.length;
        int sum = -1;
        int i = 0;
        for (; i < n; i++) {
            //若两数相同，则异或等于 0
            //若两数不同，则异或不等于 0，说明此时 i 即为缺席的同学学号
            sum = i ^ records[i];
            if (sum != 0) {
                return i;
            }
        }
        //代码走到这，说明缺少的是最后一位学号
        return i;
    }
}

解法四：数学（高斯求和公式）

//数学（高斯求和公式，也就是等差数列求和公式
class Solution {
    public int takeAttendance(int[] records) {
        int n = records.length;
        //等差数列求和公式：首项 + 尾项 乘以 项数 除以 2
        int sum = (0 + n) * (n + 1) / 2;
        //让所有学号之和 减去 当前数组中存在的学号，剩下的就是缺席的
        for (int i = 0; i < n; i++) {
            sum -= records[i];
        }
        return sum;
    }
}

前四种解法的时间复杂度都是 $O(N)$

解法五：二分查找（时间复杂度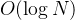： $O(\log N)$ ）

算法原理：

代码实现：

class Solution {
    public int takeAttendance(int[] records) {
        int n = records.length;
        int left = 0;
        int right = n - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (records[mid] == mid) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        //处理数组中缺少最后一个元素的情况
        if (records[left] == left) {
            return left + 1;
        }
        return left;
    }
}