代码随想录训练营 Day62打卡 图论part11
Floyd 算法
例题:卡码97. 小明逛公园
题目描述
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
输入描述
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
输出描述
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
输入示例
7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4
输出示例
4
-1
提示信息
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
本题要求使用 Floyd-Warshall 算法 解决 多源最短路径 问题,具体来说,要计算每两个景点之间的最短路径。与之前学过的 Dijkstra 或 Bellman-Ford 算法不同,Floyd-Warshall 可以处理多个起点和多个终点之间的最短路径,且适用于权值为正或负的边,但不允许存在负权回路。
核心思想
Floyd-Warshall 算法的核心思想
Floyd-Warshall 算法的核心思想是通过动态规划,逐步引入中间节点来优化路径。对于每个可能的中间节点 k,检查通过该中间节点的路径是否比原有的直接路径更短。如果更短,则更新路径长度。
具体地,假设我们有 N 个节点,Floyd-Warshall 算法可以通过三重循环来计算所有节点对之间的最短路径:
- 外层循环枚举所有可能的中间节点 k。
- 中间两层循环枚举起点 i 和终点 j,并检查是否通过中间节点 k 能找到更短的路径。
递推公式为:
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j])
其中:
grid[i][j] 表示节点 i 到节点 j 的最短路径。
grid[i][k] + grid[k][j] 表示通过中间节点 k 走到 j 的路径长度。
我们取两者的最小值,来不断更新最短路径。
遍历顺序
外层 k 遍历中间节点。内层 i, j 遍历所有起点和终点。
代码实现
if __name__ == '__main__':
max_int = 10005 # 设置一个非常大的数表示节点之间不可达
# 读取节点数 n 和边数 m
n, m = map(int, input().split())
# 初始化二维数组 grid,存储最短路径,初始值为无穷大
grid = [[max_int] * (n + 1) for _ in range(n + 1)]
# 自己到自己的最短路径为 0
for i in range(1, n + 1):
grid[i][i] = 0
# 读取边的信息,双向边,初始化各边的距离
for _ in range(m):
p1, p2, w = map(int, input().split())
grid[p1][p2] = min(grid[p1][p2], w) # 避免多条边,取最短边
grid[p2][p1] = min(grid[p2][p1], w)
# 使用 Floyd-Warshall 算法更新所有节点对之间的最短路径
for k in range(1, n + 1):
for i in range(1, n + 1):
for j in range(1, n + 1):
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j])
# 读取 Q 个查询,输出最短路径
q = int(input()) # 观景计划数量
for _ in range(q):
start, end = map(int, input().split())
if grid[start][end] == max_int:
print(-1) # 不可达
else:
print(grid[start][end]) # 输出最短路径
卡码题目链接
题目文章讲解
A * 算法
例题:97. 小明逛公园
题目描述
在象棋中,马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
输入描述
第一行包含一个整数 n,表示测试用例的数量,1 <= n <= 100。
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
输出描述
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
输入示例
6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6
输出示例
2
4
6
5
1
0
提示信息
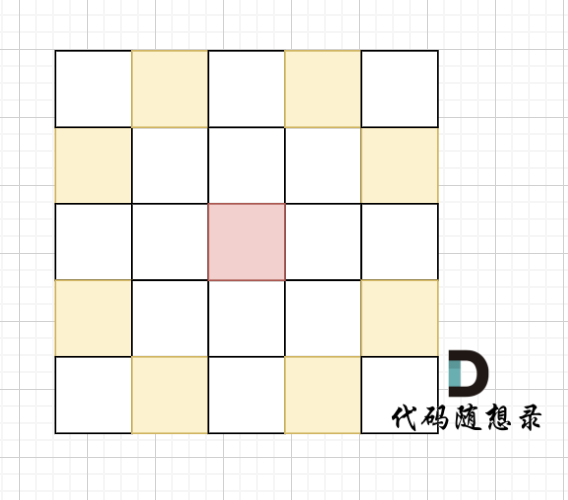
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
实现思路
本题是典型的求最短路径问题。棋盘为1000x1000,我们需要计算骑士(象棋中的“马”)从起始位置移动到目标位置所需的最短步数。
骑士的移动规则:骑士每次可以向8个不同方向移动,具体为“日”字形移动方式:即每次水平或垂直移动两格,同时在垂直或水平方向再移动一格。
A*算法:A算法是一种启发式搜索算法,使用估计代价函数来加速路径搜索。在A中,优先队列会根据状态的代价(F = G + H)来排序。
- G是从起点到当前节点的实际代价(即步数)。
- H是当前节点到目标节点的估计代价(启发式函数),可以使用欧几里得距离的平方来估算,避免开根号的浮点运算。
具体步骤:
- 定义骑士的8个可能移动方向。
- 使用优先队列(最小堆)存储每个状态,根据F值(G+H)进行排序,F值越小优先级越高。
- 初始化状态:将起点加入优先队列,开始A*搜索。
- 扩展节点:从优先队列中取出F值最小的节点,检查是否到达目标点。如果没有到达,则继续将其8个可能的移动加入优先队列。
- 剪枝:对于越界的点或已经访问过的点,跳过处理。
- 最终输出结果:当找到目标点时,输出最短步数。
代码实现
import heapq
# 定义骑士的8个移动方向
dir = [(-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2)]
# 启发式函数,计算当前节点到目标节点的估计代价(使用欧几里得距离的平方)
def heuristic(x1, y1, x2, y2):
return (x1 - x2) ** 2 + (y1 - y2) ** 2
# A*算法函数,返回从起点到终点的最短路径
def astar(a1, a2, b1, b2):
# 初始化棋盘,用于记录每个点的最短路径步数
moves = [[0] * 1001 for _ in range(1001)]
# 定义优先队列,初始加入起点
pq = []
heapq.heappush(pq, (0, a1, a2)) # (F值, x, y)
# 处理队列,开始A*搜索
while pq:
f, x, y = heapq.heappop(pq)
# 如果当前点已经到达目标点,返回步数
if x == b1 and y == b2:
return moves[x][y]
# 扩展当前点的8个移动方向
for dx, dy in dir:
nx, ny = x + dx, y + dy
# 判断是否越界
if 1 <= nx <= 1000 and 1 <= ny <= 1000:
if moves[nx][ny] == 0: # 如果该点还没有访问过
moves[nx][ny] = moves[x][y] + 1 # 更新步数
g = moves[nx][ny] * 5 # G值,每次移动的代价是5
h = heuristic(nx, ny, b1, b2) # 计算启发式估计值H
f = g + h # 计算F值
heapq.heappush(pq, (f, nx, ny)) # 将新状态加入优先队列
return -1 # 如果无法到达目标点
# 处理输入输出
if __name__ == "__main__":
n = int(input()) # 读取测试用例数量
for _ in range(n):
a1, a2, b1, b2 = map(int, input().split()) # 读取起点和终点坐标
if a1 == b1 and a2 == b2:
print(0) # 如果起点和终点相同,步数为0
else:
print(astar(a1, a2, b1, b2)) # 输出从起点到终点的最短步数
代码详解:
-
dir:定义骑士的8个移动方向。
-
heuristic:启发式函数,计算当前节点到目标节点的欧几里得距离的平方,作为H值。
-
astar:A*搜索算法的核心函数:
使用heapq实现优先队列,按F值排序。
对于每个扩展节点,检查是否越界或已经访问过。
使用G值(步数*5)和H值计算F值,并加入优先队列。 -
输入输出处理:循环处理多个测试用例,每个测试用例根据起点和终点坐标,调用A*算法求解。
时间复杂度:
最坏情况下,骑士可能需要遍历整个1000x1000的棋盘,时间复杂度约为O(NlogN),其中N是棋盘的大小,logN来自优先队列操作。
卡码题目链接
题目文章讲解