---

• 原题链接：295. 数据流的中位数

---

1- 思路

题目识别

• 识别1 ：实现一个数据结构，求中位数

堆实现

思路

• 利用优先队列，小根堆放较小的元素。
• 大根堆放较大的元素。
• 例如 1 2 3 4 5 6 ，其中大根堆放的元素是 1 2 3，小根堆放的元素是 4 5 6。中位数就是 (3+4)/2

实现

• ① 当是偶数
  • 先入小根堆，之后大根堆添加小根堆堆顶元素。
• ② 当是奇数
  • 先入大根堆，之后小根堆添加大根堆堆顶元素。

---

2- 实现

⭐4. 寻找两个正序数组的中位数——题解思路

class MedianFinder {

    Queue<Integer> min;
    Queue<Integer> max;
    public MedianFinder() {
        min = new PriorityQueue<>((x,y) -> (y-x));
        max = new PriorityQueue<>();
    }
    
    public void addNum(int num) {
        if(min.size() == max.size()){
            min.add(num);
            max.add(min.poll());
        }else{
            max.add(num);
            min.add(max.poll());
        }
    }
    
    public double findMedian() {
        if(min.size() == max.size()){
            return (min.peek()+max.peek())/2.0;
        }else{
            return max.peek()*1.0;
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

---

3- ACM 实现

package Daily_LC.Month9_Week3.Day157;

import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;

/**
 * findMid
 *
 * @author alcohol
 * @Description
 * @since 2024-09-17 12:38
 */
public class findMid {

    static Queue<Integer> min;
    static Queue<Integer> max;

    public findMid(){
        min = new PriorityQueue<>((x,y) -> (y-x));
        max = new PriorityQueue<>();
    }

    public static void add(int num){
        if(min.size() == max.size()){
            min.add(num);
            max.add(min.poll());
        }else{
            max.add(num);
            min.add(max.poll());
        }
    }

    public static double getMid(){
        if(min.size() == max.size()){
            return (min.peek()+max.peek())*0.5;
        }else{
            return max.peek()*1.0;
        }
    }

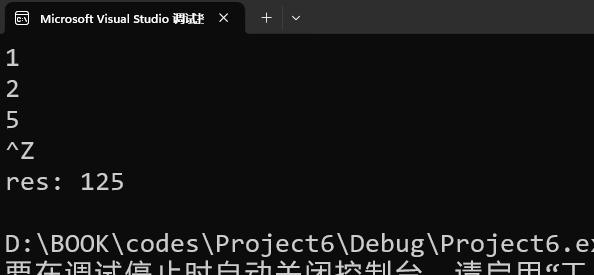
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        sc.nextLine(); // 消耗换行符
        findMid fm = new findMid();

        for(int i = 0 ; i < n ; i ++){
            String ope = sc.nextLine();
            if(ope.equals("addNum")){
                System.out.println("输入添加的数");
                int num = sc.nextInt();
                sc.nextLine(); // 消耗换行符
                fm.add(num);
            }else if(ope.equals("findMedian")){
                System.out.println(fm.getMid());
            }
        }
    }
}