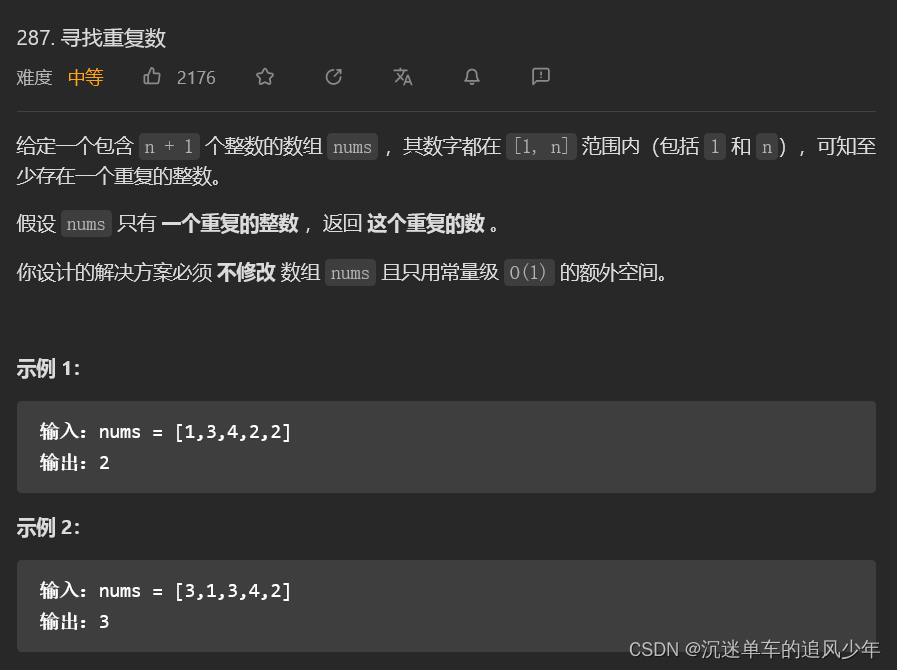
题意:
给定
n
n
n个区间
[
L
i
,
R
i
]
[L_i,R_i]
[Li,Ri]设集合
A
=
{
{
p
i
}
∣
p
i
为排列,
L
i
<
=
p
i
<
=
R
i
}
A=\{ \{ p_i\} | p_i为排列,Li<=p_i<=R_i\}
A={{pi}∣pi为排列,Li<=pi<=Ri},让你求
∣
A
∣
m
o
d
2
|A| \mod 2
∣A∣mod2。
思路:
这道题在比赛的时候被卡了很久,我尝试猜各种结论,但是发现都行不通。导致了整个比赛的节奏很糟糕。
后面突然发现可以转换成行列式来做,就是第 i i i行的 L i L_i Li到 R i R_i Ri列全部填1,其它都是0,求这个行列式的奇偶性。
然后我就想着左端点相同的可以用最短的来消元,然后用线段树合并来维护。
赛后得知这是一个很常见的套路,但自己感觉能想到行列式已经非常的不容易。而且求解行列式可以建立n+1个点,给点 L i L_i Li和 R i + 1 R_i+1 Ri+1连边,判断是不是树即可。原理就是线性相关的几个行向量系数都是1和-1,就相当于往左跳或者往右跳。
最令人难过的是,我在一本竞赛书里面查积分表的时候发现旁边已经写了这个结论。。。