MATLAB 可视化基础：绘图命令与应用

news2024/9/20 16:50:59

1. 绘制子图

1.1基本绘图命令

首先，我们使用 linspace 函数生成一个在 0 到 3 之间均匀分布的 20 个点。接着，我们定义了线性、二次和三次方函数，并将它们绘制在同一图中。

x = linspace(0, 3, 20); % 在 0 到 3 之间等距取 20 个点
y1 = x;                  % y1 = x
y2 = x.^2;               % y2 = x^2
y3 = x.^3;               % y3 = x^3

% 绘制图形
plot(x, y1, 'red-', x, y2, 'blue*--', x, y3, 'black-o');
set(gca, 'xlim', [0 3], 'xtick', [0:0.1:3]); % 设置 x 轴范围和刻度
set(gca, 'color', 'none'); % 背景色设置为无色
title('示意图');          % 图形标题
xlabel('x的变化');        % x 轴标签
ylabel('y的变化');        % y 轴标签
text(0.5, 25, '说明示例', 'fontname', '宋体'); % 添加注释
legend('线性y=x', '二次方y=x^2', '三次方y=x^3', 'location', 'northeast'); % 图例
box off;                  % 半框
axis square;             % 产生正方形坐标系

其中：
plot 函数用于绘制数据曲线，支持不同的颜色和样式。
set(gca,…) 用于设置坐标轴属性。
legend 提供图例，帮助识别不同的数据系列。

1.2. 使用 subplot 函数

在同一窗口中，我们可以使用 subplot 函数将绘图区域分为多个子图。以下是绘制三角函数的示例：


x = 0:0.1:2*pi; % x 从 0 到 2π
y1 = sin(x);    % 正弦
y2 = cos(x);    % 余弦
y3 = tan(x);    % 正切
y4 = sin(x) .* cos(x); % 正弦乘余弦

subplot(2, 2, 1);
plot(x, y1, 'blacko'); % 第一子图：正弦函数
subplot(2, 2, 2);
plot(x, y2, 'ro');     % 第二子图：余弦函数
subplot(2, 2, 3);
plot(x, y3, 'bo');     % 第三子图：正切函数
subplot(2, 2, 4);
plot(x, y4, 'go');     % 第四子图：正弦乘余弦

其中
subplot(m, n, p) 将图形窗口分为 m 行 n 列的子图，并激活第 p 个子图。
每个子图可以独立绘制不同的数据，便于比较。

1.3. 绘图类型

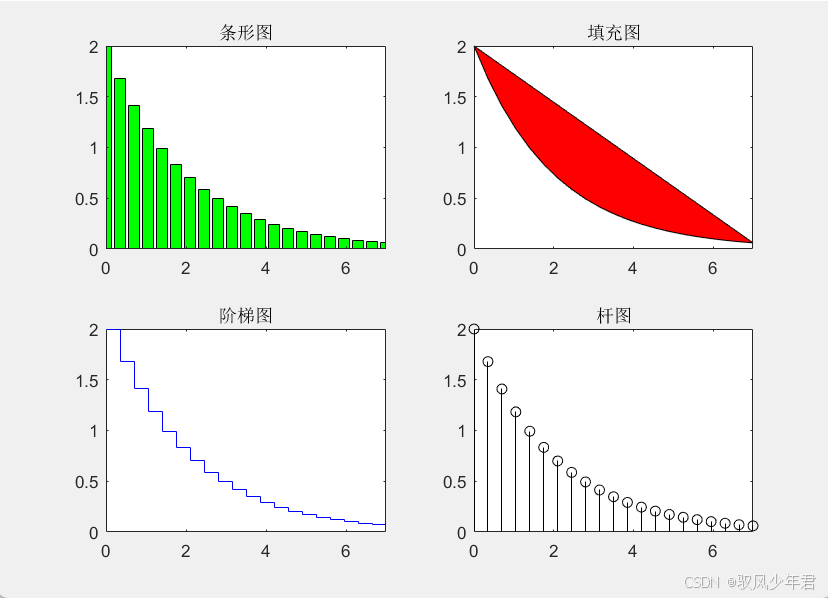
MATLAB 还支持多种绘图类型，例如条形图、填充图、阶梯图和杆图。以下是这些图形的示例：


x = 0:0.35:7;
y = 2 * exp(-0.5 * x); % 指数衰减函数

subplot(2, 2, 1);
bar(x, y, 'g');         % 条形图
title('条形图');
axis([0, 7, 0, 2]);

subplot(2, 2, 2);
fill(x, y, 'r');       % 填充图
title('填充图');
axis([0, 7, 0, 2]);

subplot(2, 2, 3);
stairs(x, y, 'b');     % 阶梯图
title('阶梯图');
axis([0, 7, 0, 2]);

subplot(2, 2, 4);
stem(x, y, 'k');       % 杆图
title('杆图');
axis([0, 7, 0, 2]);

bar 绘制条形图，适合展示离散数据的分布。
fill 创建填充图，适合展示区域数据。
stairs 和 stem 分别绘制阶梯图和杆图，常用于显示离散数据的变化。

在这里插入图片描述

2.MATLAB 可视化进阶(以下代码均居于以上代码的数据定义上实现)

在 MATLAB 中的一些高级绘图技巧，包括极坐标图、对数坐标图和隐函数的绘制。这些技术将帮助您更好地展示和分析数据。

2.1. 极坐标图

极坐标图是以极坐标系而非直角坐标系绘制数据的一种方式，适合展示与角度和半径相关的数据。


theat = 0:0.1:2*pi; % 角度范围
y1 = sin(1/2 * theat); % 第一个极径
y2 = sin(theat) .* cos(theat); % 第二个极径

subplot(2, 2, 1)
plot(theat, y1, 'r'); % 第一子图：直角坐标系下的极径
subplot(2, 2, 2)
plot(theat, y2, 'b'); % 第二子图：直角坐标系下的极径
subplot(2, 2, 3)
polar(theat, y1, 'r'); % 第三子图：极坐标图
grid on; % 开启网格
subplot(2, 2, 4)
polar(theat, y2, 'b'); % 第四子图：极坐标图
grid on; % 开启网格

解释
polar 函数用于绘制极坐标图，输入参数为角度和极径。
通过 subplot 函数，我们可以在一个窗口中展示多个图形，使得比较不同数据集变得更加直观。
在这里插入图片描述

对数坐标图
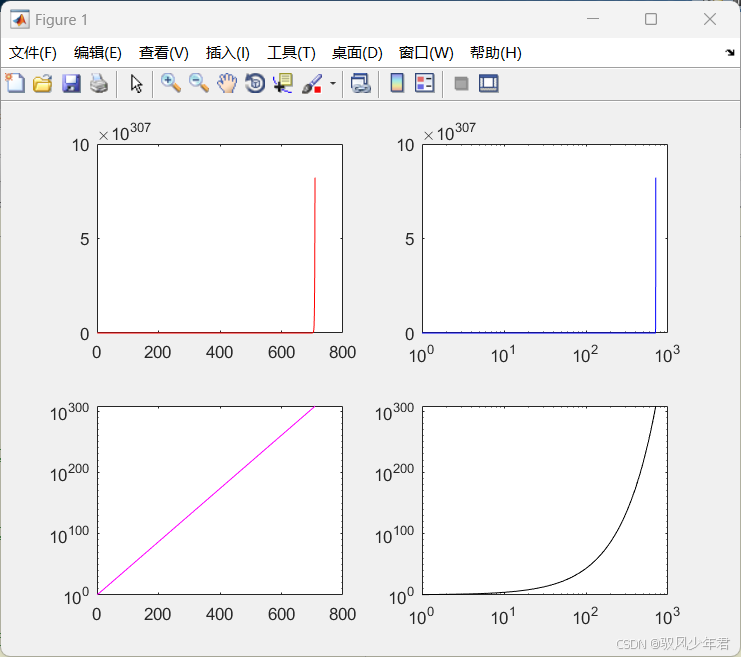
对数坐标图有助于展示数据的指数增长，适用于展示范围较大的数据值。

x = 1:1000; 
y = x.^2 + exp(x); % 计算 y 值

subplot(2, 2, 1)
plot(x, y, 'r-'); % x 轴线性，y 轴线性
subplot(2, 2, 2)
semilogx(x, y, 'b-'); % x 轴对数，y 轴线性
subplot(2, 2, 3)
semilogy(x, y, 'm-'); % x 轴线性，y 轴对数
subplot(2, 2, 4)
loglog(x, y, 'k-'); % x 轴对数，y 轴对数

解释
semilogx 和 semilogy 分别用于绘制 x 轴对数和 y 轴对数的图形。
loglog 函数绘制 x 轴和 y 轴均为对数坐标的图形，适合展示指数级增长的数据。

在这里插入图片描述

2.3. 隐函数的绘制

MATLAB 的 ezplot 函数可以方便地绘制隐函数和参数方程。

subplot(3, 1, 1)
ezplot('sin(x)', [0, 2*pi]); % 显函数 y=f(x)
subplot(3, 1, 2)
ezplot('cos(x) + sin(y)', [-2, 2, -2, 2]); % 隐函数 f(x,y)=0
subplot(3, 1, 3)
ezplot('3*t', 'sin(t)', [0, 2*pi]); % 参数方程 x=f(t), y=f(t)