MATLAB系列02：MATLAB基础

2. MATLAB基础
- 2.1 变量和数组
- 2.2 MATLAB变量的初始化
- - 2.2.1 用赋值语句初始化变量
  - 2.2.2 用捷径表达式赋值
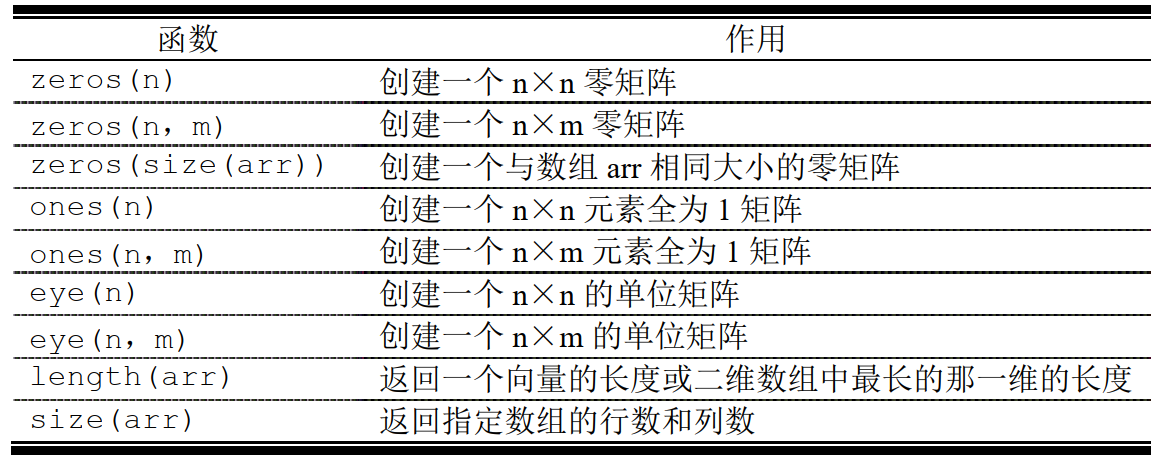
  - 2.2.3 使用内置函数来初始化
  - 2.2.4 使用关键字input来初始化
- 2.3 多维数组
- - 2.3.1 创建多维数组
  - 2.3.2 多维数组在内存中的存储
  - 2.3.3 用单个下标访问多标数组
- 2.4 子数组
- - 2.4.1 end函数
  - 2.4.2 子数组在左边的赋值语句的使用
  - 2.4.3 用一标量给子数组赋值
- 2.5 特殊变量
- 2.6 显示输出数据
- - 2.6.1 改变默认格式
  - 2.6.2 disp函数
  - 2.3.3 使用fprintf函数格式化输出数据
- 2.7 数据文件
- 2.8 标量运算和数组运算
- - 2.8.1 标量运算符
  - 2.8.2 数组运算和矩阵运算
- 2.9 运算的优先级
- 2.10 MATLAB的内建函数
- - 2.10.1 选择性结果
  - 2.10.2 带数组输入的MATLAB函数的应用
  - 2.10.3 常见的MATLAB函数
- 2.11 画图入门
- - 2.11.1 简单的xy画图
  - 2.11.2 打印图像
  - 2.11.3 联合作图
  - 2.11.4 线的颜色，线的形式，符号样式和图例
  - 2.11.5 对数尺度
- 2.12 调试MATLAB程序

2. MATLAB基础

2.1 变量和数组

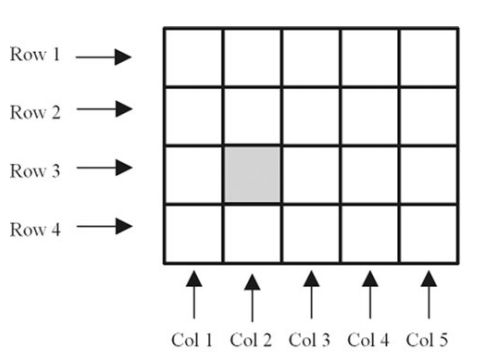
MATLAB程序的基本数据单元是数组。一个数组是以行和列组织起来的数据集合，并且拥有一个数组名。数组中的单个数据是可以被访问的，访问的方法是数组名后带一个括号，括号内是这个数据所对应行标和列标。标量在 MATLAB 中也被当作数组来处理——它被看作只有一行一列的数组。

数组可以定义为向量或矩阵。向量一般用来描述一维数组，而矩阵往往用来描述二维或多维数组。

数组的大小（size）由数组的行数和列数共同决定，注意行数在前。一个数组所包含的数据多少可由行数乘列数得到。

数组的访问：

>> A=[1 2 ;3 4 ;5 6]

A =

     1     2
     3     4
     5     6

>> A(2,1)

ans =

     3

MATLAB的变量名必须以字母开头，后面可以跟字母，数组或下划线，不能超过31个字符。

编程隐患：

必须确保所声明的变量名前31个字符是独一无二的，否则MATLAB无法辨认出它们的不同

当编写程序时，给变量起一个有意义的名字十分重要。可以在所写程序开头列出一数据字典，列举在本程序中用到所有变量的定义。在MATLAB中，是区分字母大小的，要小心使用。一个好的编程习惯是在变量名中只使用小写字母。

在MATLAB中，最常见的两种变量类型是char型和double型。double型变量包括64位双精度浮点数构成的标量或数组，这种变量可以代表实数，虚数和复数。每个值的实部和虚部的变化范围为 $±10−308 \pm10^{-308}\sim10^{308}$ ，拥有15到16位的有效数字。char型变量包括由16位数值构成的标量或数组，每16位数代表一个字符。

MATLAB是弱类型语言，通过简单的赋值形式就可以创建变量，变量类型取决于创建时的类型。

2.2 MATLAB变量的初始化

MATLAB初始化变量的三种方式

用赋值语句初始化变量
用input函数从键盘输入初始化变量
从文件中读取一个数据

2.2.1 用赋值语句初始化变量

赋值语句的一般形式

var=expression

在一行内单个数值用空格或逗号隔开，行与行之间用分号隔开或另起一行书写。

示例：

语句	含义
[3,4]	创建一个 $1\times 1$ 数组，这时括号可以省略
[1.0 2.0 3.0 ]	创建一个 $1\times 3$ 数组，一维向量 $[1\,2\,3]$
[1.0 ;2.0;3.0]	创建一个 $3\times 1$ 向量，一维向量 $\begin{bmatrix}1\\2\\3\end{bmatrix}$

编程隐患：

每一行元素的个数必须完全相同，每一列元素的个数也必须完全相同

当创建一个数组时，并不是每个元素都必须定义，没有被定义的元素会自动创建并初始化为0，例如

>> c(2,3)=5

c =

     0     0     0
     0     0     5

赋值语句有分号和没有分号的区别：如果赋值语句后面没有分号，变量值会自动显示在命令窗口，如果有分号，将会中止变量值在命令窗口的重复。一般赋值我们都会加上分号，在调试时可以把分号去掉。

2.2.2 用捷径表达式赋值

MATLAB提供一种专门的捷径标记法，一般顺序如下：

first:incr:last

first代表数组第一个值，incr代表步长，last代表数组最后一个值，如果步长为1，可以省略。示例：

>> x=1:2:10

x =

     1     3     5     7     9

>> g=[1:4]'
h=[g g]

g =

     1
     2
     3
     4


h =

     1     1
     2     2
     3     3
     4     4

2.2.3 使用内置函数来初始化

2.2.4 使用关键字input来初始化

如果输入一个数，那么只需要之间输入；如果要输入一个数组，必须带上中括号。如果input中有字符’s’作为它的第二个参数，则输入的数据被当作字符串处理。示例：

>> my_val=input('Enter a value：')
Enter a value：1.23

my_val =

    1.2300

>> my_val=input('Enter a value：','s')
Enter a value：1.23

my_val =

    '1.23'

2.3 多维数组

2.3.1 创建多维数组

MATLAB允许我们创建多维数组，这些数组每一维对应一个下标，示例：

>> c(:,:,1)=[1,2,3;4,5,6];
c(:,:,2)=[7,8,9;10,11,12];
whos c
  Name      Size             Bytes  Class     Attributes

  c         2x3x2               96  double              

>> c

c(:,:,1) =

     1     2     3
     4     5     6


c(:,:,2) =

     7     8     9
    10    11    12

2.3.2 多维数组在内存中的存储

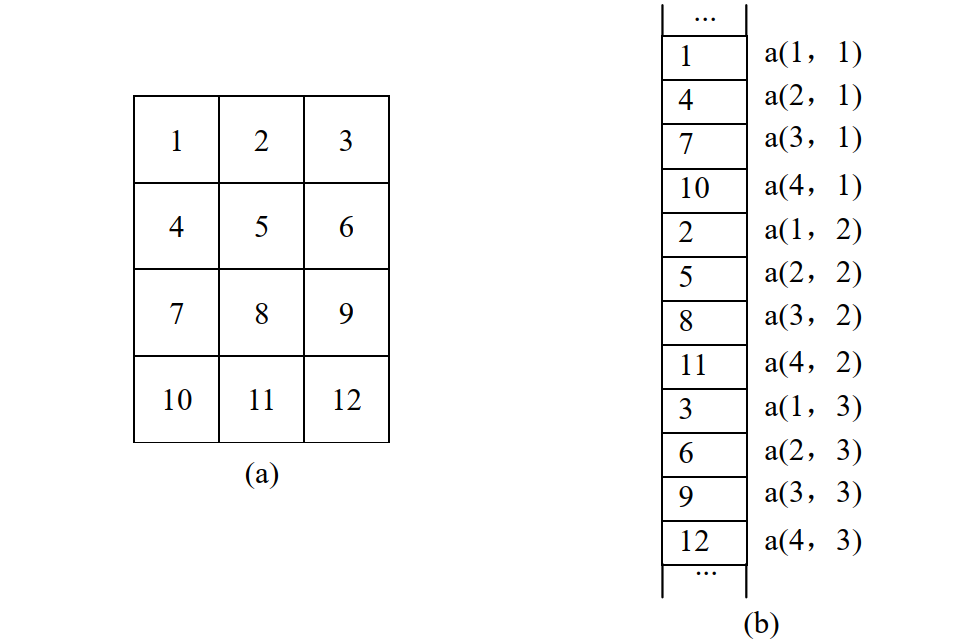
在内存中，MATLAB以列主导顺序分配数组中的元素，先分配第一列，然后第二列，第三列，…以此类推

2.3.3 用单个下标访问多标数组

MATLAB 的特性之一就是它允许使用者或程序员把一个多维数看作一个一维数组，这个一维数组的长度等于多维数组的元素数。如果用一个下标访问一个多维数组，那么元素的排列顺序就是内存的分配顺序。例如我们声明一个 $4\times 3$ 数组如下：

>> a=[1 2 3; 4 5 6;7 8 9;10 11 12]

a =

     1     2     3
     4     5     6
     7     8     9
    10    11    12

>> a(1,2)

ans =

     2

>> a(5)

ans =

     2

我们可以看到a(1,2)的值和a(5)的值是一样的。因为a(1,2)在内存中排第5。

在一般情况下，我们不应该使用MATLAB这一特性。用单个下标访问多维数组会带来很多麻烦。

2.4 子数组

在数组名后面加括号，括号里面是所有要选择的元素的下标，这样就能选择这个函数的子集了，例如：

>> arr=[1 2 3;-2 -3 -4;3 4 5]

arr =

     1     2     3
    -2    -3    -4
     3     4     5

>> arr(:,1:2:3)

ans =

     1     3
    -2    -4
     3     5

2.4.1 end函数

MATLAB 中有一个特殊的函数叫做 end 函数，对于创建子数组的下标非常的有用.当用到一个函数的下标时， end 函数将会返回下标的最大值，例如：

>> arr=[1 2 3 4 5 6 7 8];
>> arr(5:end)

ans =

     5     6     7     8

>> arr(end)

ans =

     8

2.4.2 子数组在左边的赋值语句的使用

只要数组的形（行数和列数）和子数组的形相匹配，把子数组放于赋值语句的左边用来更新数组中的值。如果形不匹配，那么将会有错误产生。例如：

>> arr=[1 2 3 4;5 6 7 8;9 10 11 12]

arr =

     1     2     3     4
     5     6     7     8
     9    10    11    12

>> arr(1:2,[1 4])=[20 21;22 23]

arr =

    20     2     3    21
    22     6     7    23
     9    10    11    12

编程隐患：

对于涉及子数组的赋值语句，等号两边的形必须相匹配，否则会产生错误

2.4.3 用一标量给子数组赋值

位于赋值语句的右边的标量值总是能匹配左边数组的形。这个标量值将会被复制到左边语句中所对应的元素。示例：

>> arr(1:2,1:2)=100

arr =

   100   100     3     4
   100   100     7     8
     9    10    11    12

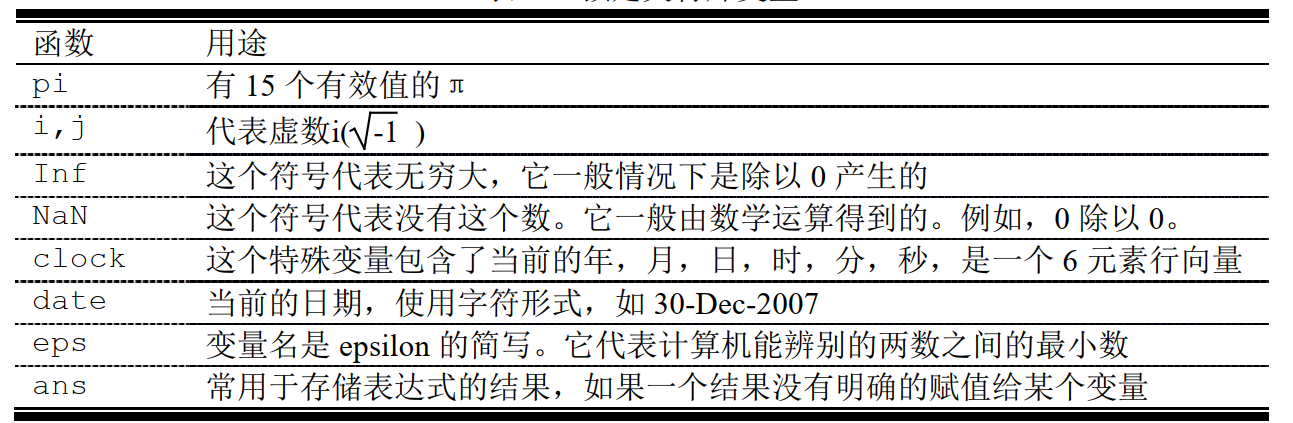
2.5 特殊变量

在 MATLAB 中有许多预先定义好的特殊变量。在 MATLAB 中这些特殊变量可以随时使用，不用初始化。

编程隐患：

不要重定义有意义的预定义变量，否则后患无穷，制造出小而难以发现的错误。

2.6 显示输出数据

最简单的方法是去掉语句末的分号。还有一些其他方法。

2.6.1 改变默认格式

当数据重复在命令窗口时，整数以整形形式显示，其他值将以默认格式显示。 MATLAB 的默认格式是精确到小数点后四位。如果一个数太大或太小，那么将会以科学记数法的形式显示。例如：

>> x=100.11

x =

  100.1100

>> z=0.00010011

z =

   1.0011e-04

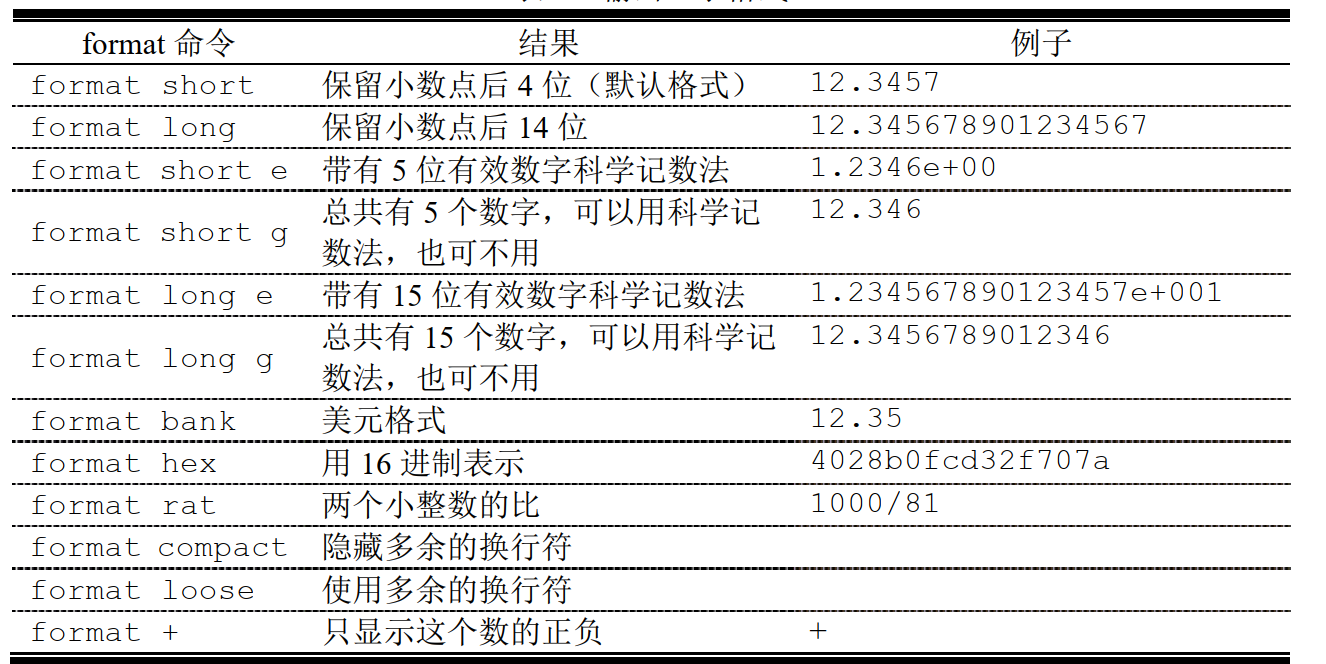
改变默认输出格式要用format命令，可参考下表。

2.6.2 disp函数

disp需要一个数组参数，此函数可联合num2str和int2str来产生新的信息，示例：

>> str=['the value of pi=',num2str(pi)];
>> disp(str)
the value of pi=3.1416

2.3.3 使用fprintf函数格式化输出数据

一般格式如下：

fprintf(format,data)

示例：

>> fprintf('the value of pi is %6.2f \n',pi)
the value of pi is   3.14

转义序列%6.2 代表在本函数中的第一个数据项将占有 6 个字符宽度，小数点后有 2 位小数。

fprintf 函数有一个重大的局限性，只能显示复数的实部。当我们的计算结果是复数时，这个局限性将会产生错误。在这种情况下，最好用 disp 显示数据。

fprintf函数format字符中的特殊字符如下：

编程隐患：

fprintf函数只能显示复数的实部，所以在有复数参加或产生的计算中，可能产生错误的结果

2.7 数据文件

最简单的加载和保存命令是save和load。

save 命令用于保存当前 MATLAB 工作区内的数据到一个硬盘文件。这个命令的基本形式如下

save filename var1 var2 var3

filename 代表你要保存变量的那个文件， var1， var2 等是要保存的变量。在默认情况下，这个文件的扩展名为“mat”，我们称之为 MAT 文件。如果在 filename 后面无变量，则工作区的所有内容将会被保存。

MATLAB 用一种特殊的复杂形式来存储数据，包括了许许多多的细节，例如变量名和变量类型，数组的大小，以及所有变量值。一个在任何一个平台上创建的 MAT 文件(pc， mac， unix)在另一个平台上都可以应用。它的缺点是 MAT 文件的存储格式不能被其他程序读取。如果一个数据必须由其他程序所读取，那么必须转化为 ASCII 码，并将这些数值写到一个以 ASCII 码为编码的文件中。但是，当以 ASCII 的形式存储，像变量名和变量类型这样的信息就会丢失，产生的数据结果将会更大。

例如，假设数组 x 的定义如下

x=[1.23 3.14 6.28; -5.1 7.00 0];

命令save x.dat x -ascii将会创建一个文件 x.dat，包括数据如下

1.2300000e+000 3.1400000e+000 6.2800000e+000
-5.1000000e+000 7.0000000e+000 0.0000000e+000

load 命令与 save 命令相反。它从硬盘文件加载数据到 MATLAB 当前工作区。这个命令的基本格式为

load filename

MATLAB 能够加载由其他程序创建的 ASCII 格式的数据文件。它首先检查所要加载的文件是 mat 文件还是 ASCII 文件。如果在 load 语句中加入 ASCII 中，则强制 MATLAB 把这个文件看作 ASCII 文件。这个文件的内容将会被转化为一个 MATLAB 的数组，这个数组名就所要加载的文件名。

2.8 标量运算和数组运算

在MATLAB中赋值语句中的计算的一般形式：

variable_name=expression

赋值语句计算出等号右边表达式的值，然后赋值于等号左边的变量名。

2.8.1 标量运算符

2.8.2 数组运算和矩阵运算

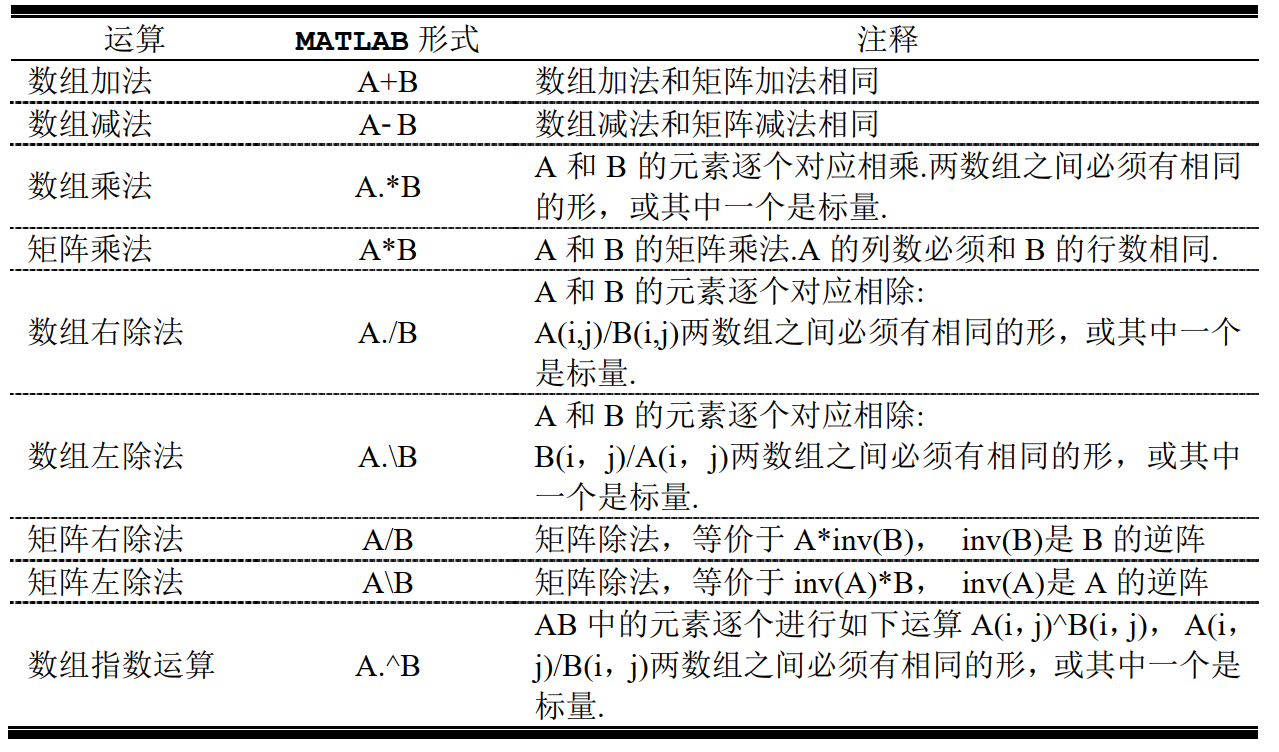
MATLAB在数组运算中提供了两种不同类型的运算，一种是数组运算(array operations)，一种是矩阵运算(matrix)。数组运算是一种用于元素对元素的运算，相对地，矩阵运算则遵守线性代数的一般规则。

MATLAB 用一个特殊的符号来区分矩阵运算和数组运算。在需要区分两者不同的时侯，把点置于符号前来指示这是一个数组运算。

编程隐患：

在MATLAB代码中，仔细区分数组运算和矩阵运算，数组乘法和矩阵乘法极易混淆。

2.9 运算的优先级

2.10 MATLAB的内建函数

2.10.1 选择性结果

MATLAB 函数返回一个或多个值给调用函数。 max 函数就是这样的一个例子。这个函数一般情况下返回输入向量中的最大值，但是它返回的第二个参数是输入向量中的最大值在向量中的位置。例如

>> maxval=max([0,1,2])

maxval =

     2

>> [maxval,index]=max([0,1,2])

maxval =

     2


index =

     3

2.10.2 带数组输入的MATLAB函数的应用

许多 MATLAB 函数定义了一个或多个标量输入，产生一个输出。示例：

>> x=[0 pi/2 3*pi/2 2*pi];
y=sin(x)

y =

         0    1.0000   -1.0000   -0.0000

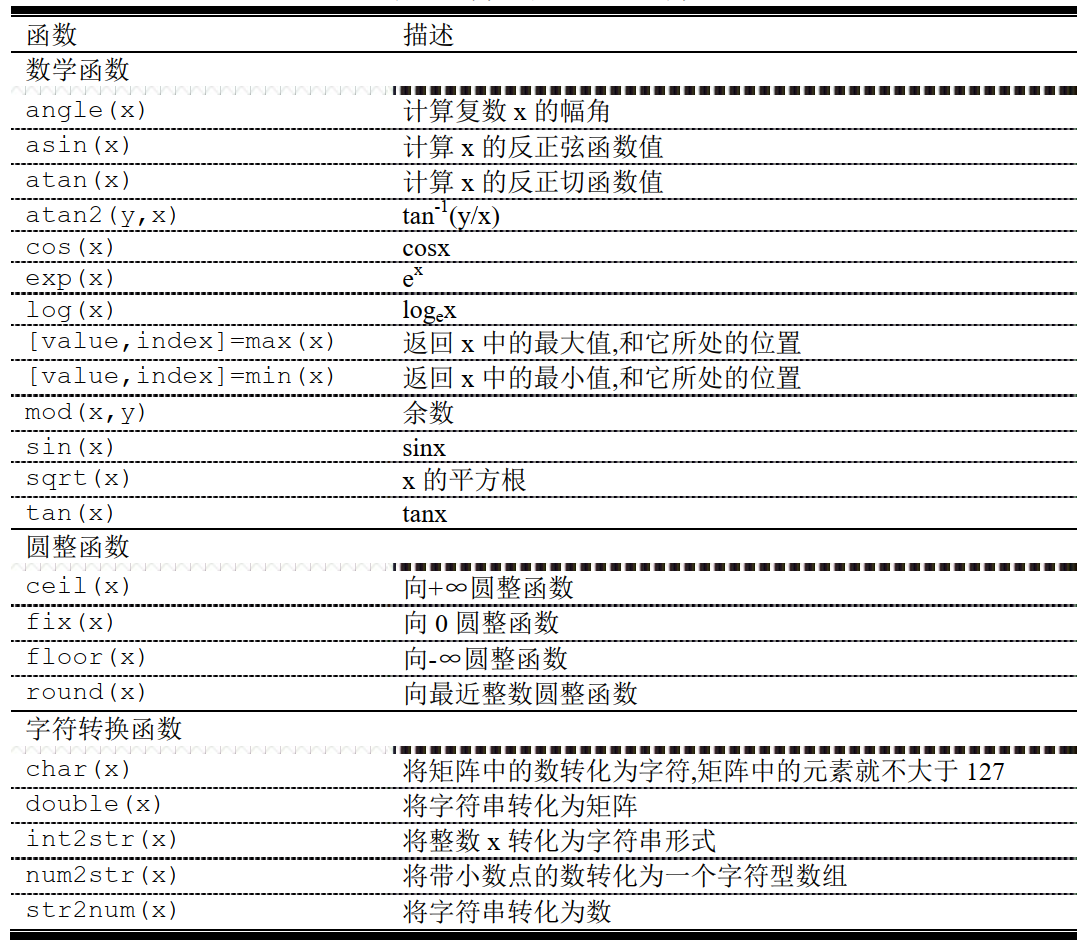
2.10.3 常见的MATLAB函数

注意：与大多数语言不同，许多MATLAB函数能够正确计算出复数结果，示例：

>> sqrt(-2)

ans =

   0.0000 + 1.4142i

2.11 画图入门

2.11.1 简单的xy画图

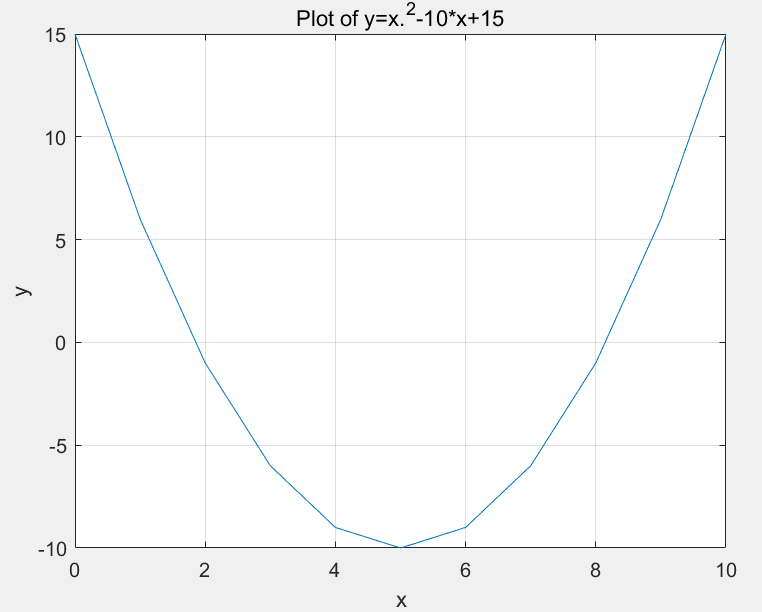
x=0:1:10;
y=x.^2-10*x+15;
plot(x,y);
title ('Plot of y=x.^2-10*x+15');
xlabel ('x');
ylabel ('y');
grid on;

2.11.2 打印图像

一个图像一旦建立，我们就可以用 print 命令在打印机上打印出这幅图，也可以单击图像窗口的打印图标或者在文件菜单中选择打印项打印。print 命令的一般形式如下：

print <选项> <文件名>

如果没有文件名，这个命令就会命令打印机打印当前图片。如果带有文件名，那么这个命令就会打印这个图片到指定的文件。有许多的选项指定输出到文件或打印机的格式。一个最重要的选项是-dtiff.这个选项指定输出图片的格式是标签影像档案格式（ TIFF）。因为PC， Mac 和 UNIX 平台上的文字处理软件都支持这种格式。这就使得在文档中插入 MATLAB 图像变得十分的简单。下面这个命令将会创建一个 TIFF 格式的当前图像的图片，并保存在一个叫my_image.tif 的文件中

print –dtiff my_image.tif

你也可以选择图象窗口中的“file/export”选项来创建 tiff 图片。

2.11.3 联合作图

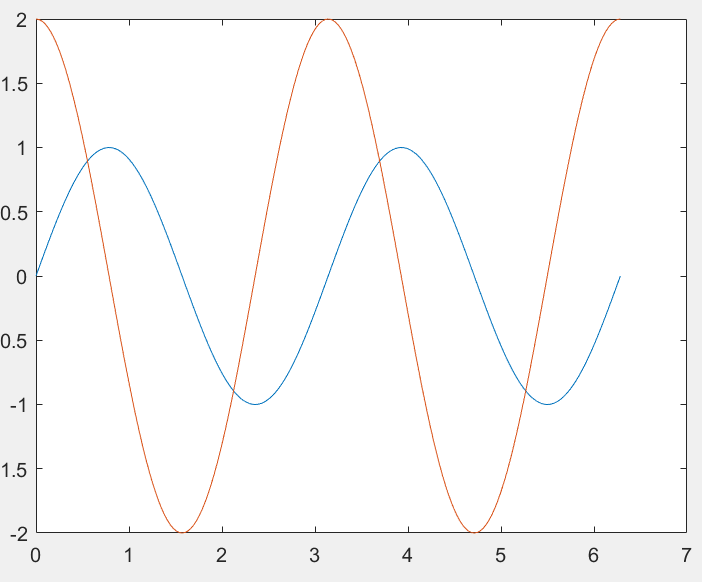
x = 0:pi/100:2*pi;
y1 = sin(2*x);
y2 = 2*cos(2*x);
plot (x,y1,x,y2);

2.11.4 线的颜色，线的形式，符号样式和图例

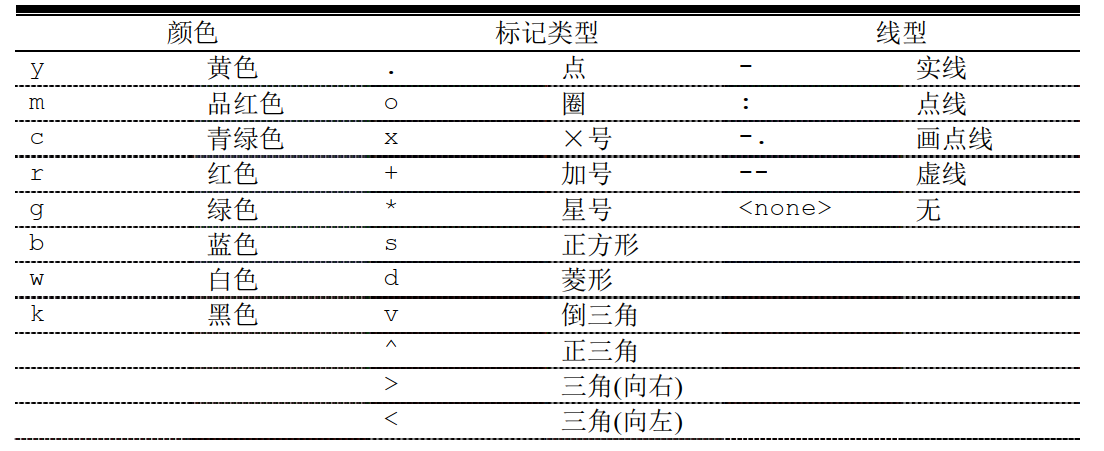
使用示例：

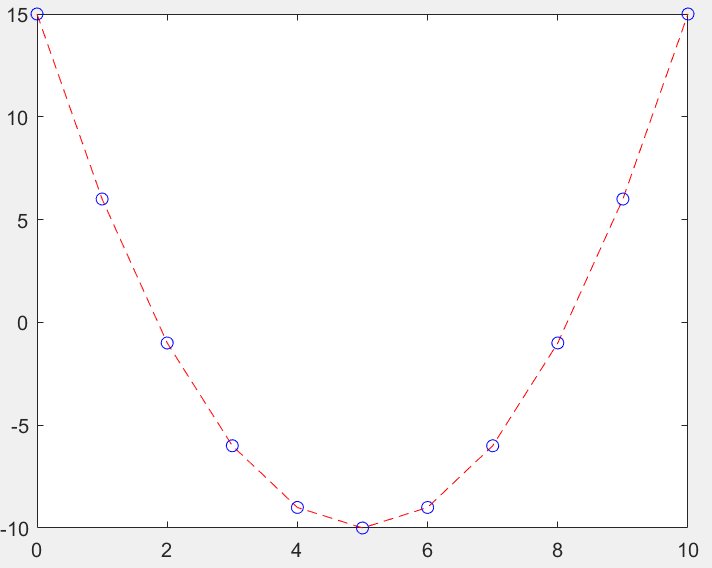
x = 0:1:10;
y = x.^2 -10.*x +15;
plot(x,y,'r--',x,y,'bo')

可以使用legend来制作图例

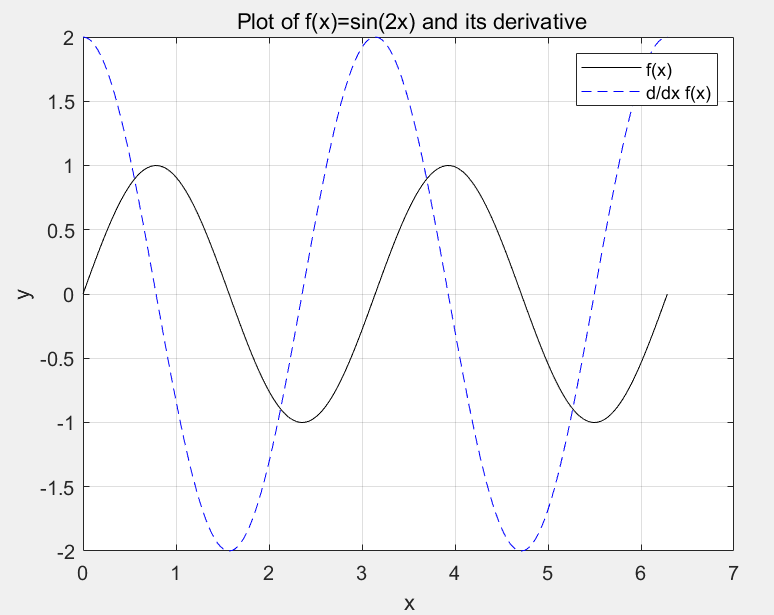
x=0:pi/100:2*pi;
y1=sin(2*x);
y2=2*cos(2*x);
plot(x,y1,'k-',x,y2,'b--');
title(' Plot of f(x)=sin(2x) and its derivative');
xlabel('x');
ylabel('y');
legend('f(x)','d/dx f(x)')
grid on;