代码随想录训练营 Day60打卡图论part10 SPFA算法 Bellman-Ford 之判断负权回路 Bellman-Ford 之单源有限最短路

代码随想录训练营 Day60打卡图论part10

一、Bellman_ford 队列优化算法（又名SPFA）

例题：卡码94. 城市间货物运输 I

题目描述
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。
输入描述
第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v （单向图）。
输出描述
如果能够从城市 1 到连通到城市 n，请输出一个整数，表示运输成本。如果该整数是负数，则表示实现了盈利。如果从城市 1 没有路径可达城市 n，请输出 “unconnected”。
输入示例
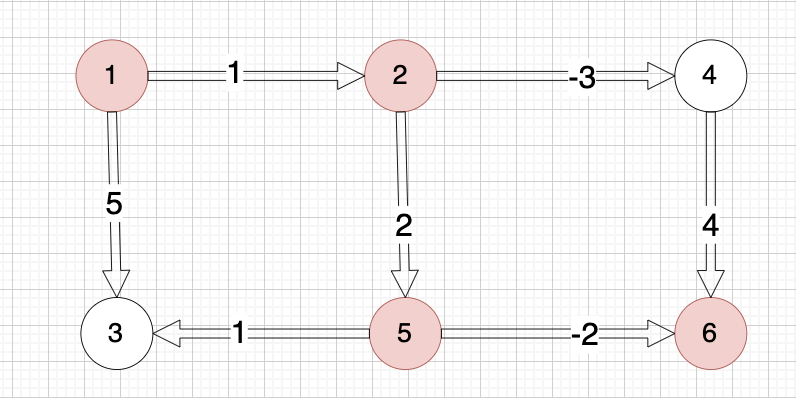
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
输出示例
1
提示信息

示例中最佳路径是从 1 -> 2 -> 5 -> 6，路上的权值分别为 1 2 -2，最终的最低运输成本为 1 + 2 + (-2) = 1。
示例 2：
4 2
1 2 -1
3 4 -1
在此示例中，无法找到一条路径从 1 通往 4，所以此时应该输出 “unconnected”。

SPFA（Shortest Path Faster Algorithm）是一种 Bellman-Ford 算法的队列优化版本。它的主要思想是：使用一个队列来保存已经更新过的节点，并且仅对这些节点进行松弛操作，而不是对所有边进行松弛，从而加速最短路径的计算。这样可以减少不必要的松弛操作。

算法流程

初始化距离数组，将起点的距离设为 0，其他节点的距离设为正无穷大。将起点加入队列。
每次从队列中取出一个节点，遍历与该节点相连的所有边，如果可以进行松弛，则更新相邻节点的最短路径，并将该相邻节点加入队列（如果它不在队列中的话）。
重复步骤 3，直到队列为空。

代码实现

from collections import deque, defaultdict
import sys

# 定义一个边结构，用于存储每条边的信息
class Edge:
    def __init__(self, to, weight):
        self.to = to  # 边的目标节点
        self.weight = weight  # 边的权重

def spfa(n, edges, start, end):
    # 初始化邻接表
    graph = defaultdict(list)
    for p1, p2, val in edges:
        graph[p1].append(Edge(p2, val))

    # 初始化最短距离数组，所有节点的最短距离都为无穷大
    minDist = [sys.maxsize] * (n + 1)
    minDist[start] = 0  # 起点的距离设为0

    # 初始化队列，并将起点加入队列
    queue = deque([start])
    isInQueue = [False] * (n + 1)  # 用于记录节点是否在队列中，避免重复加入
    isInQueue[start] = True

    while queue:
        # 从队列中取出一个节点
        node = queue.popleft()
        isInQueue[node] = False  # 节点取出后取消标记

        # 遍历该节点的所有相邻边，进行松弛操作
        for edge in graph[node]:
            to = edge.to
            weight = edge.weight
            # 如果可以通过 node 到达 to 的更短路径，则更新最短距离
            if minDist[to] > minDist[node] + weight:
                minDist[to] = minDist[node] + weight
                # 如果相邻节点不在队列中，则将其加入队列
                if not isInQueue[to]:
                    queue.append(to)
                    isInQueue[to] = True

    # 如果终点的最短距离仍为无穷大，说明无法到达终点
    if minDist[end] == sys.maxsize:
        print("unconnected")
    else:
        print(minDist[end])  # 输出到终点的最短路径长度

# 输入处理
n, m = map(int, input().split())  # n 是节点数，m 是边数
edges = []
for _ in range(m):
    p1, p2, val = map(int, input().split())  # 输入边信息
    edges.append((p1, p2, val))

start = 1  # 起点设为节点1
end = n    # 终点设为节点n

# 调用SPFA算法
spfa(n, edges, start, end)

详细解释：

Edge类：定义了一个边结构，用于存储边的目标节点和边的权重。
spfa 函数：这是 SPFA 算法的主体函数，接收节点数 n、边列表 edges、起点 start 和终点 end作为参数，返回从起点到终点的最短路径距离。
graph：邻接表，用来存储每个节点的相邻边。
minDist：最短距离数组，初始时所有节点的最短距离都设置为无穷大，起点的最短距离为 0。
queue：队列，用于存储更新过的节点，起点首先加入队列。
isInQueue：标记数组，表示当前节点是否在队列中，避免重复入队。
while 循环：不断从队列中取出节点并进行松弛操作，直到队列为空。
松弛操作：如果通过某条边可以找到更短路径，则更新目标节点的最短路径，并将其加入队列。
最终结果：如果终点的最短路径值仍为无穷大，则表示无法到达终点；否则输出终点的最短路径长度。

复杂度分析：

时间复杂度：最坏情况下时间复杂度为 O(V * E)，其中 V 为节点数，E 为边数。但由于队列优化，通常性能会比原始的
Bellman-Ford 更优。
空间复杂度：O(V + E)，用来存储图和队列。

SPFA 的优化机制
SPFA 的核心优化思想是只松弛那些可能带来改进的边。它使用队列来跟踪已经发生更新的节点（称为活跃节点），从这些节点出发继续尝试松弛邻接边。这样就避免了对所有边的重复松弛。

关键优化点：

只松弛有效边：

Bellman-Ford 每一轮都会检查所有边，而 SPFA 只松弛从“活跃节点”出发的边。这意味着在很多情况下，SPFA 需要松弛的边数量会远小于 Bellman-Ford 的所有边。

跳过不活跃节点：

只有当某个节点的最短路径被更新时，SPFA 才会将它的相邻节点加入队列。因此，如果某些节点的路径没有更新，它们不会被加入队列进行松弛操作。

动态松弛顺序：

Bellman-Ford 是静态的，每一轮都对所有边进行遍历；而 SPFA 是动态的，按需对队列中的节点及其相邻边进行松弛。这种按需松弛会根据路径变化自适应调整执行顺序，减少无效计算。

时间复杂度分析

最坏情况：

在最坏情况下，SPFA 可能需要对每条边执行 𝑉次松弛操作，这样最坏情况下的时间复杂度仍然是：𝑂(𝑉×𝐸)
这与 Bellman-Ford 算法在最坏情况下一样。
平均情况：

在许多实际应用中，SPFA 通常可以在远少于 𝑉−1 轮迭代的情况下收敛。这是因为一旦最短路径收敛，队列中的节点数量会迅速减少，因此减少了不必要的松弛操作。对于稀疏图（边较少）和具有良好结构的图，SPFA 的平均时间复杂度更接近于线性：𝑂(𝐸) 。
也就是只需对每条边松弛一次或几次即可收敛。

卡码题目链接
题目文章讲解

二、Bellman-Ford 之判断负权回路

例题：卡码94. 城市间货物运输 I

题目描述
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
然而，在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时，存在一种情况：图中可能出现负权回路。负权回路是指一系列道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴，算法还需检测这种特殊情况。
请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
城市 1 到城市 n 之间可能会出现没有路径的情况
输入描述
第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。
输出描述
如果没有发现负权回路，则输出一个整数，表示从城市 1 到城市 n 的最低运输成本（包括政府补贴）。如果该整数是负数，则表示实现了盈利。如果发现了负权回路的存在，则输出 “circle”。如果从城市 1 无法到达城市 n，则输出 “unconnected”。
输入示例
4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
输出示例
circle
提示信息
路径中存在负权回路，从 1 -> 2 -> 3 -> 1，总权值为 -1，理论上货物运输商可以在该回路无限循环赚取政府补贴，所以输出 “circle” 表示已经检测出了该种情况。

Bellman-Ford 算法是一种用于寻找图中单源最短路径的算法，允许图中存在负权边，但不能处理图中存在负权回路的情况。在 Bellman-Ford 算法中，松弛每条边 n-1 次（n 是节点数）可以确保找到从起点到所有其他节点的最短路径。如果在第 n 次松弛后仍然发生了变化，说明图中存在负权回路。

负权回路的影响

在本题中，由于存在负权回路，我们可以在回路中绕圈，继续减小路径的代价，导致最短路径可以无限减小。这意味着存在负权回路的图是没有最小路径解的，因为可以通过绕圈使路径代价无限减少。因此，解决本题的关键在于：在执行完 n-1 次松弛之后，再执行第 n 次松弛，如果最短路径数组 minDist 仍然发生变化，则说明存在负权回路。

思路总结

初始化：从起点到其他所有节点的距离初始化为无穷大（inf），到起点自身的距离为 0。
松弛过程：对所有边进行 n-1 次松弛操作，确保找到从起点到其他节点的最短路径。
判断负权回路：在第 n 次松弛时，如果距离数组发生变化，则说明图中存在负权回路。

代码实现

import sys

def main():
    input = sys.stdin.read
    data = input().split()
    index = 0
    
    # 读取节点数 n 和边数 m
    n = int(data[index])
    index += 1
    m = int(data[index])
    index += 1
    
    # 记录所有的边，grid 是一个包含 [p1, p2, val] 的列表，表示从 p1 到 p2，权值为 val
    grid = []
    for i in range(m):
        p1 = int(data[index])
        index += 1
        p2 = int(data[index])
        index += 1
        val = int(data[index])
        index += 1
        grid.append([p1, p2, val])

    start = 1  # 起点是节点 1
    end = n    # 终点是节点 n

    # minDist 数组存储起点到每个节点的最短距离，初始为无穷大
    minDist = [float('inf')] * (n + 1)
    minDist[start] = 0  # 起点到自身的距离为 0
    flag = False  # 用于标记是否有负权回路

    # 松弛 n 次，前 n-1 次是正常的 Bellman-Ford 松弛，第 n 次用于检查负权回路
    for i in range(1, n + 1):  # 从 1 到 n，松弛 n 次
        for side in grid:
            from_node = side[0]  # 边的起点
            to = side[1]         # 边的终点
            price = side[2]      # 边的权值
            
            # 如果松弛次数小于 n 次，正常松弛
            if i < n:
                # 如果起点到 from_node 的距离不是无穷大，且通过 from_node 能到达 to，并且能更新到更小的距离，则进行松弛
                if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:
                    minDist[to] = minDist[from_node] + price
            else:
                # 第 n 次松弛，用于检查是否存在负权回路
                if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:
                    flag = True  # 如果还能松弛，说明存在负权回路

    # 如果存在负权回路
    if flag:
        print("circle")
    # 如果起点和终点不连通，即终点的最短路径还是无穷大
    elif minDist[end] == float('inf'):
        print("unconnected")
    else:
        # 否则输出起点到终点的最短路径
        print(minDist[end])

if __name__ == "__main__":
    main()

卡码题目链接
题目文章讲解

三、Bellman-Ford 之单源有限最短路

例题：卡码96. 城市间货物运输 III

题目描述
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。
输入描述
第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。
最后一行包含三个正整数，src、dst、和 k，src 和 dst 为城市编号，从 src 到 dst 经过的城市数量限制。
输出描述
输出一个整数，表示从城市 src 到城市 dst 的最低运输成本，如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径，则输出 “unreachable”，表示不存在符合条件的运输方案。
输入示例
6 7
1 2 1
2 4 -3
2 5 2
1 3 5
3 5 1
4 6 4
5 6 -2
2 6 1
输出示例
0
提示信息
从 2 -> 5 -> 6 中转一站，运输成本为 0。

本题是 Bellman-Ford 算法的一个变种，需要计算从起点到终点，**最多经过 k 个城市（即 k + 1 条边）**的最短路径。核心思想和 Bellman-Ford 算法类似，不同之处在于我们需要限制松弛操作的次数，即最多只松弛 k + 1 次。

问题背景

每次松弛操作，相当于对所有边进行一次松弛，尝试更新当前已知的最短路径。
在标准的 Bellman-Ford 中，我们对所有边松弛 n-1 次即可得到从起点到所有其他节点的最短路径，其中 n
是节点数量，因为最长路径最多经过 n-1 条边。
而在本题中，我们只需要考虑最多经过 k + 1 条边的路径，因此只需松弛 k + 1 次。

问题关键
在松弛过程中，更新节点的距离时，我们要基于上一次松弛后的最短路径来进行更新。因此，每次松弛时要基于前一次的结果（即 minDist_copy 数组）进行更新，而不是当前的结果。

思路总结

初始化 minDist 数组，表示从起点到各个节点的最短路径，起点到自身距离为 0，其他节点初始化为无穷大（表示不可达）。
松弛 k + 1 次，每次松弛时基于上一次松弛的结果更新最短路径。
在松弛结束后，如果终点的最短路径依然为无穷大，说明不可达，输出 “unreachable”。否则输出最短路径。

代码实现

import sys

def main():
    input = sys.stdin.read
    data = input().split()
    
    # 读取节点数 n 和边数 m
    index = 0
    n = int(data[index])
    index += 1
    m = int(data[index])
    index += 1
    
    # 读取边信息 (p1, p2, val)
    grid = []
    for i in range(m):
        p1 = int(data[index])
        index += 1
        p2 = int(data[index])
        index += 1
        val = int(data[index])
        index += 1
        grid.append([p1, p2, val])
    
    # 读取起点 src，终点 dst，最多经过的节点数 k
    src = int(data[index])
    index += 1
    dst = int(data[index])
    index += 1
    k = int(data[index])
    index += 1
    
    # 初始化最短路径数组，minDist[src] = 0 表示起点到自身的距离为 0
    minDist = [float('inf')] * (n + 1)
    minDist[src] = 0
    
    # 用来记录上一次遍历的最短路径结果
    minDist_copy = minDist[:]
    
    # 松弛 k + 1 次
    for i in range(k + 1):
        minDist_copy = minDist[:]  # 记录上一次松弛的最短路径结果
        for side in grid:
            from_node = side[0]
            to_node = side[1]
            price = side[2]
            # 如果 from_node 可达，并且可以更新到更短的路径，更新 minDist
            if minDist_copy[from_node] != float('inf') and minDist[to_node] > minDist_copy[from_node] + price:
                minDist[to_node] = minDist_copy[from_node] + price
    
    # 输出结果
    if minDist[dst] == float('inf'):
        print("unreachable")  # 如果终点不可达，输出 unreachable
    else:
        print(minDist[dst])   # 否则输出起点到终点的最短路径

if __name__ == "__main__":
    main()

时间复杂度：本算法的时间复杂度为 O(k * m)，其中 k 是松弛次数，m 是图中边的数量。相较于标准的 Bellman-Ford 算法时间复杂度 O(n * m)，这是合理的限制条件，因为我们只松弛 k + 1 次。
空间复杂度：主要存储 minDist 和 minDist_copy 两个数组，空间复杂度为 O(n)。

卡码题目链接
题目文章讲解