参考:https://baijiahao.baidu.com/s?id=1803373544569190578&wfr=spider&for=pc
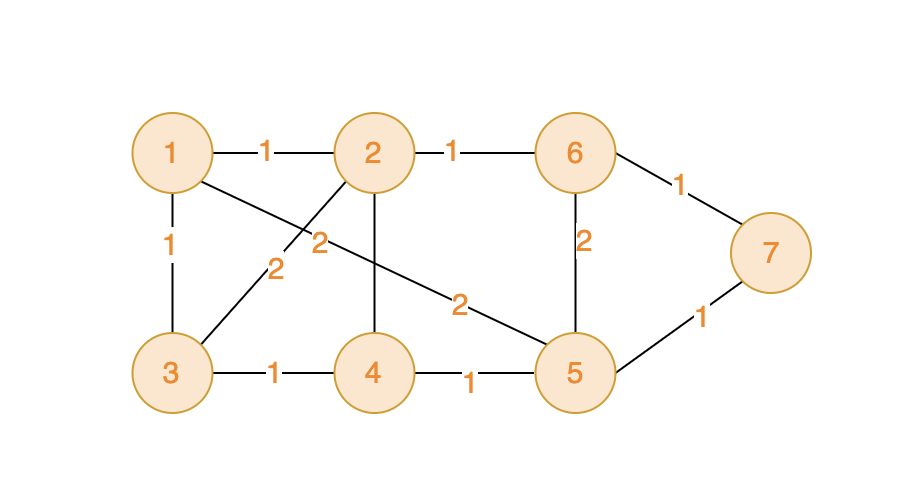
IP-Adapter 是 SD中比较重要的controlnet,由腾讯公司出品。主要原理:提取图像特征,并嵌入预训练文本,最终加入到扩散图像中。简单理解,提取图像的特征:构图特征、面部特征,根据权重参数与原prompt进行融合,共同作用到扩散图像上。
以下面这张图举例:
从条件图中提取特征,包括前景、背景结构,任务特征等。

简单案例:https://blog.csdn.net/qq_41314882/article/details/140517620
其中也有讲述InstanID的内容,结论:在面部处理上InstantID 优于 IP-Adapter
相关文档:https://baijiahao.baidu.com/s?id=1806079149555811709&wfr=spider&for=pc










![AV1 Bitstream Decoding Process Specification--[3]:约定](https://i-blog.csdnimg.cn/direct/92e21056c5c84460b4797ce0e85e94fd.png)