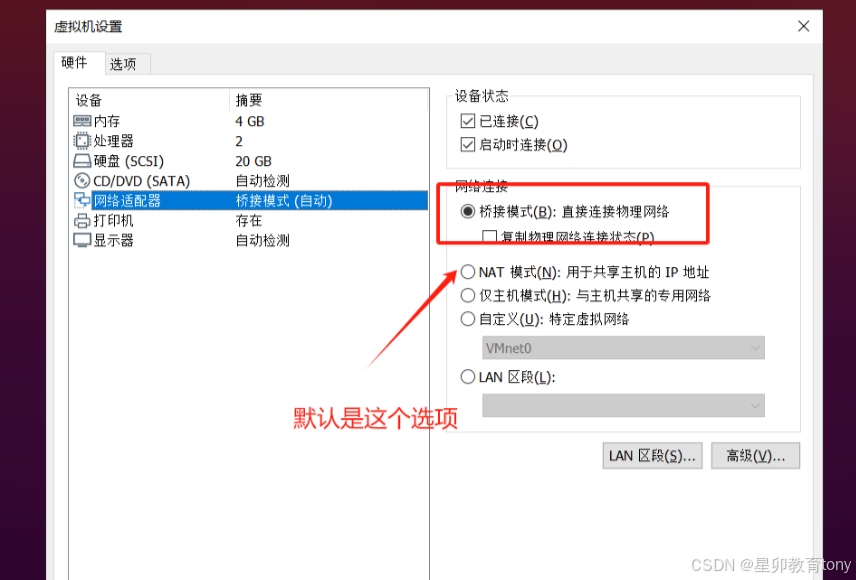
由于 subsingleton 使用函数（eliminator） 的存在，导致算法式相等（Algorithm defintional equality）的非传递性。

在《定义上相等的非确定性（Undecidability of Definitional Equality）》 中有，

其中，定义上相等可替换规则起来作用：

同时，根据 归纳类型（Inductive Type）的简化规则（Reduction Rule），有：

简单来看是，intro 0 inv 0 a 的类型为 acc 0，而 inv 0 a 1 (p 0) 的类型为 acc 1，即两者的类型不同。由此，

实际上是，可达类型（Accessibility Type）中，

其使用规则定义的使用函数，是 subsingleton 使用函数（eliminator）：

        这里，由于可达类型（Accessibility Type）的 subsingleton 使用函数（eliminator）在使用前值、前果时，由于前值与现值不属于同一类型，即 acc n 和 acc (n+1)，因此，有，

        但是，f 0 a 没有使用规则（Elimination Rule）用于产生 f 1 (inv 0 a 1 ( p 0 ) )，也没有已经定义的简化规则可以使用，因此，

        在LEAN的设计上，算法式定义上相等是可确定的（Decidable），而定义上相等是不确定的（undecidable），由此，有些定义上相等的推演规则是没有对应的算法式定义上相等的规则，如 传递性（transitivity）只存在于定义上相等，也导致了其不确定性，即在判断定义上相等时，会陷入不能停止（non-terminated）。

        这里需要明确的是，LEAN系统内的所有能使用的转化规则，赋型规则等，都必须是LEAN显示（Explicit）定义的。