1. 力扣2807:在链表中插入最大公约数
1.1 题目:
你一个链表的头 head ,每个结点包含一个整数值。
在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。
请你返回插入之后的链表。
两个数的 最大公约数 是可以被两个数字整除的最大正整数。
示例 1:

输入:head = [18,6,10,3] 输出:[18,6,6,2,10,1,3] 解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。 - 18 和 6 的最大公约数为 6 ,插入第一和第二个结点之间。 - 6 和 10 的最大公约数为 2 ,插入第二和第三个结点之间。 - 10 和 3 的最大公约数为 1 ,插入第三和第四个结点之间。 所有相邻结点之间都插入完毕,返回链表。
示例 2:

输入:head = [7] 输出:[7] 解释:第一幅图是一开始的链表,第二幅图是插入新结点后的图(蓝色结点为新插入结点)。 没有相邻结点,所以返回初始链表。
提示:
- 链表中结点数目在
[1, 5000]之间。 1 <= Node.val <= 1000
1.2 思路
这题的难点在于如果求两个相邻节点的最大公约数。如果两个值中的最大值可以与最小值整除,那么最小值就是最大公约数,否则我们用更相减损术(夸克搜的)。
1.3 题解:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode insertGreatestCommonDivisors(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode dummy = new ListNode(10086, head);
ListNode cur = dummy;
// 用来求最大公约数
while(cur.next != null && cur.next.next != null){
int a = cur.next.val;
int b = cur.next.next.val;
int max = Integer.max(a, b);
int min = Integer.min(a, b);
// 如果可以整除,最小值就是最大公约数
if(max % min == 0){
} else {
// 更相减损术
int sub = max - min;
while(sub != min){
max = Integer.max(sub, min);
min = Integer.min(sub, min);
sub = max - min;
}
}
ListNode p = new ListNode(min, cur.next.next);
cur.next.next = p;
// 这里是p的原因在于:我们要处理的是cur的下一个节点和下下一个节点
// 而p此时位于的节点刚好在要处理的两个节点前面
cur = p;
}
return dummy.next;
}
}2. 力扣LCR:029:循环有序列表的插入
2.1 题目:
给定循环单调非递减列表中的一个点,写一个函数向这个列表中插入一个新元素 insertVal ,使这个列表仍然是循环升序的。
给定的可以是这个列表中任意一个顶点的指针,并不一定是这个列表中最小元素的指针。
如果有多个满足条件的插入位置,可以选择任意一个位置插入新的值,插入后整个列表仍然保持有序。
如果列表为空(给定的节点是 null),需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点。
示例 1:

输入:head = [3,4,1], insertVal = 2
输出:[3,4,1,2]
解释:在上图中,有一个包含三个元素的循环有序列表,你获得值为 3 的节点的指针,我们需要向表中插入元素 2 。新插入的节点应该在 1 和 3 之间,插入之后,整个列表如上图所示,最后返回节点 3 。
示例 2:
输入:head = [], insertVal = 1
输出:[1]
解释:列表为空(给定的节点是 null),创建一个循环有序列表并返回这个节点。
示例 3:
输入:head = [1], insertVal = 0
输出:[1,0]
提示
0 <= Number of Nodes <= 5 * 10^4-10^6 <= Node.val <= 10^6-10^6 <= insertVal <= 10^6
2.2 思路:
先遍历链表找到链表中最新的最大值节点,该节点的next节点即该链表的最小值节点(可能会有很多个最小值节点,但该最小值节点是边界)。
从最小值节点开始遍历,碰到合适的位置就可以插入,然后返回head即可。如果直到遍历完链表,仍然找不到位置插入,该需要插入节点的值比整个链表的值都要大或都要小,则需要插入到最小值节点的后面,这个时候我们就可以想到找到该最小值节点的上一个节点,parent节点跟踪最小值节点min_point。然后处理parent节点和要插入节点的关系即可。
2.3 题解:
/*
// Definition for a Node.
class Node {
public int val;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _next) {
val = _val;
next = _next;
}
};
*/
class Solution {
public Node insert(Node head, int insertVal) {
Node insert = new Node(insertVal);
// 如果链表为空,需要特殊判断
if(head == null){
insert.next = insert;
return insert;
}
// 遍历链表找到最小值节点
// 发现最新的最大值的后面就是最小值
// 因为最大值可能有很多个,我们要最新的,所以p.val >= max有等于号
int max = head.val;
Node max_point = head;
Node p = head.next;
// n表示链表的长度
int n = 1;
while(p != head){
if(p.val >= max){
max = p.val;
max_point = p;
}
n++;
p = p.next;
}
// max_point指向了最大值的节点
Node min_point = max_point.next;
Node parent = null;
while(n-- > 0){
// 找到合适的地方就插入
if(min_point.val <= insertVal && insertVal <= min_point.next.val){
insert.next = min_point.next;
min_point.next = insert;
return head;
}
parent = min_point;
min_point = min_point.next;
}
// 还没插入成功,插到最小值后面
insert.next = parent.next;
parent.next = insert;
return head;
}
}3. 力扣147:对链表进行插入排序
3.1 题目:
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。

示例 1:
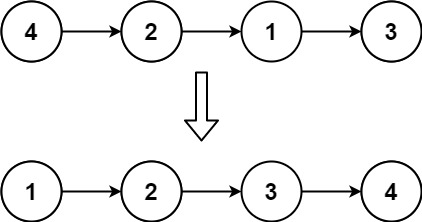
输入: head = [4,2,1,3] 输出: [1,2,3,4]
示例 2:
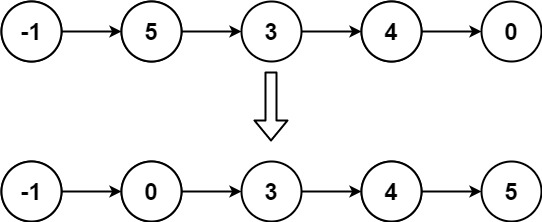
输入: head = [-1,5,3,4,0] 输出: [-1,0,3,4,5]
提示:
- 列表中的节点数在
[1, 5000]范围内 -5000 <= Node.val <= 5000
3.2 思路:
由于个人实力太菜,写着一跑就超时了,无奈转换成求解数组的插入排序。
3.3 题解
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode insertionSortList(ListNode head) {
// 特殊情况直接返回
if(head == null || head.next == null) {
return head;
}
ListNode node = head;
int n = 0;
while(node != null){
n++;
node = node.next;
}
int[] arr = new int[n];
node = head;
n = 0;
while(node != null){
arr[n++] = node.val;
node = node.next;
}
for(int i = 1; i < arr.length; i++){
int t = arr[i];
int j = i - 1;
while(j >= 0 && t < arr[j]){
arr[j+1] = arr[j];
j--;
}
if(j != i - 1){
arr[j+1] = t;
}
}
node = head;
int k = 0;
while(node != null){
node.val = arr[k++];
node = node.next;
}
return head;
}
}