散列函数

散列函数（Hash Function，又称散列算法、哈希函数），是一种从任何一种数据中创建小的数字指纹的方法。

散列值

散列函数，把任意长的消息明文，压缩成摘要，使得数据量变小，将数据的长度固定下来，这种输出的值，称为散列值或者哈希值（Hash Value）。

散列值，通常用一个短的随机字母和数字组成的字符串。

基本特性

不可逆性

这是散列函数的关键特点，从散列值无法从理论上还原出原始值，确保了数据安全。

抗碰撞性

一个好的散列算法，应该抵抗散列碰撞。

理论上，如果两个原始值是不相同的，那么他们的散列值也不相同。

但是也有概率会出现原始值不同散列值相同的情况，尤其是当输出长度有限时。

应用

数据加密

正因为散列函数拥有抗碰撞性和不可逆性，所以大多数的数据加密，可以使用散列算法。

数据完整性

通常把原数据和散列值一起发送，接收方接收到数据后，把原数据散列计算后得到的散列值和接收到的散列值比较，如果一致则证明该数据未被篡改。

散列表

散列表（Hash Table）是散列函数的一个主要应用，是一种非常高效的数据结构，主要用于存储和检索数据。

散列表通过将键（Key）映射到值（Value）来存储数据，每个键都通过特定的散列算法转为一个唯一的索引（Hash Code），然后每次查找指定的索引从而找到想要的值。

常用算法

MD5

MD5消息摘要算法（MD5 Message-Digest Algorithm），是一种广泛使用的密码散列函数，可以生成一个128位的散列值。

由MD2、MD3、MD4改进而来，主要增强算法复杂度和不可逆性。

但在1996年被证实存在弱点，可以被破解。

2004年被证实无法防止碰撞攻击，因此不适用于安全性，主要被用于SSL公开密钥认证或者数字签名等用途。

算法

MD5 是输入不定长数据，输出固定128位的算法。

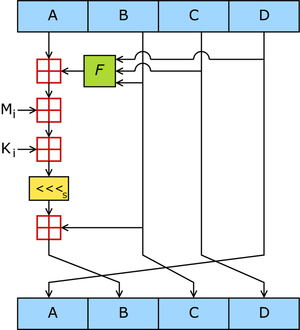
一个MD5运算，由类似的64次循环构成，分成4组16次。

• F：一个非线性函数；一个函数运算一次；
• M_i：表示一个 32-bits 的输入数据；
• K_i：表示一个 32-bits 常数，用来完成每次不同的计算。

应用场景

• 文件校验，常用于文件下载时，生成文件的MD5值，与源文件的MD5值做比较，验证文件是否完整。
• 消息摘要，由于计算速度较快，可以快速生成信息摘要的场景下使用。

示例

一般128位的MD5散列被表示为32位十六进制数字

import hashlib

text = "你好，阿一"
md5 = hashlib.md5()
md5.update(text.encode('utf-8'))
md5.hexdigest()

# 362ccc2f2b1c6635d743a08990e5f908

SHA-1

SHA-1（Secure Hash Algorithm 1，安全散列算法 1），是一种密码散列函数。

SHA-1可以生成一个被称为消息摘要的160位散列值，散列值通常的呈现形式为40个十六进制数。

2005年，密码分析人员发现了对SHA-1的有效攻击方法，表明该算法可能不够安全。2017年2月23日，CWI Amsterdam与Google宣布了一个成功的SHA-1碰撞攻击，发布了两份内容不同但SHA-1散列值相同的PDF文件作为概念证明。

应用场景

• 文件校验，校验文件是否完整，也可以校验文件的SHA-1值。
• 数字证书，曾经被作为SSL/TLS协议的签名算法。

示例

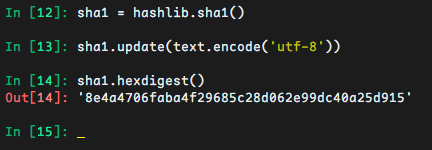
sha1 = hashlib.sha1()
sha1.update(text.encode('utf-8'))
sha1.hexdigest()

# 8e4a4706faba4f29685c28d062e99dc40a25d915

SHA-2

SHA-2（Secure Hash Algorithm 2，安全散列算法 2），2001年发布，是SHA-1的后继者，分为几个不同的算法标准，SHA-224，SHA-256，SHA-384，SHA-512，SHA-512/224，SHA-512/256。

最常用的是 SHA256，生成256位的散列值，64个十六进制表示。

算法

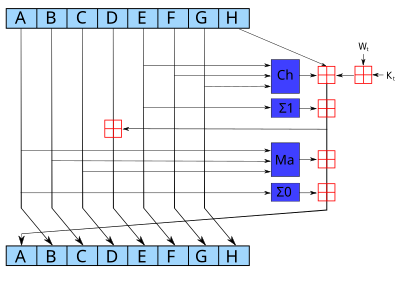
SHA-2的第t个加密循环。图中的深蓝色方块是事先定义好的非线性函数。

• ABCDEFGH一开始分别是八个初始值，K_t是第t个密钥，W_t是本区块产生第t个word。
• 原消息被切成固定长度的区块，对每一个区块，产生n个word（n视算法而定），透过重复运作循环n次对ABCDEFGH这八个工作区段循环加密。
• 最后一次循环所产生的八段字符串合起来即是此区块对应到的散列字符串。
• 若原消息包含数个区块，则最后还要将这些区块产生的散列字符串加以混合才能产生最后的散列字符串。

应用场景

• 文件校验，校验文件是否完整，也可以校验文件的SHA-256值。
• 数字证书，在数字证书和数字签名的生成过程中，SHA-256被广泛使用，提供较高的安全性和抵抗碰撞攻击的能力。
• 密码保护，需要应用程序都是用SHA-256对密码进行散列计算存储，以提高密码安全。

示例

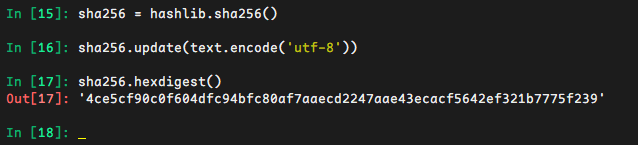
sha256 = hashlib.sha256()
sha256.update(text.encode('utf-8'))
sha256.hexdigest()

# 4ce5cf90c0f604dfc94bfc80af7aaecd2247aae43ecacf5642ef321b7775f239

SM3

SM3是我国国家密码管理局发布的一种密码散列函数算法，属于国家商用密码，算法公开。

主要用于数据签名及验证、消息认证码生成及验证、随机数生成等，安全性及效率与SHA-256相当。

生成长度位为256位的散列值。

特点

• 性能高效，计算速度非常高效，适合大规模数据处理。
• 安全性，当前没有有效的攻击手段可以破坏SM3的安全性，其抗抵赖性和抗伪造能力都符合现代加密需求。

应用场景

• 政府，信创环境
• 国内的金融系统中的数据保护和数据完整性
• 电子签名
• 与SM2配套使用，用于SM2中数字签名的随机数生成

示例

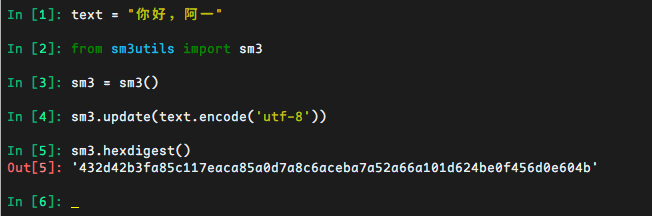
from sm3utils import sm3
sm3 = sm3()
sm3.update(text.encode('utf-8'))
sm3.hexdigest()

# 432d42b3fa85c117eaca85a0d7a8c6aceba7a52a66a101d624be0f456d0e604b

总结

本文主要简单介绍了密码散列函数算法 MD5、SHA-1、SHA-2、和 SM3 的基本原理，以及它们的实现过程。对比另外两类算法，散列函数算法最大优势就是验证完整性、散列表和数字签名。

三篇文章，对各种加密算法和应用场景进行了全面的介绍。密码学是一门深奥的学科，而作为密码学的使用者，只需要正确地理解各类算法的特性和功能，就可以满足日常的应用需求了。

总的来说，在使用的时候，要记住下面这些内容：

• 对称加密具备较高的安全性和性能，要优先考虑；
• 在一对多的场景中（如多人登录服务器），存在密钥分发难题的时候，我们要使用非对称加密；
• 不需要可逆计算的时候（如存储密码），我们就使用散列函数算法。