[实践应用] 深度学习之激活函数

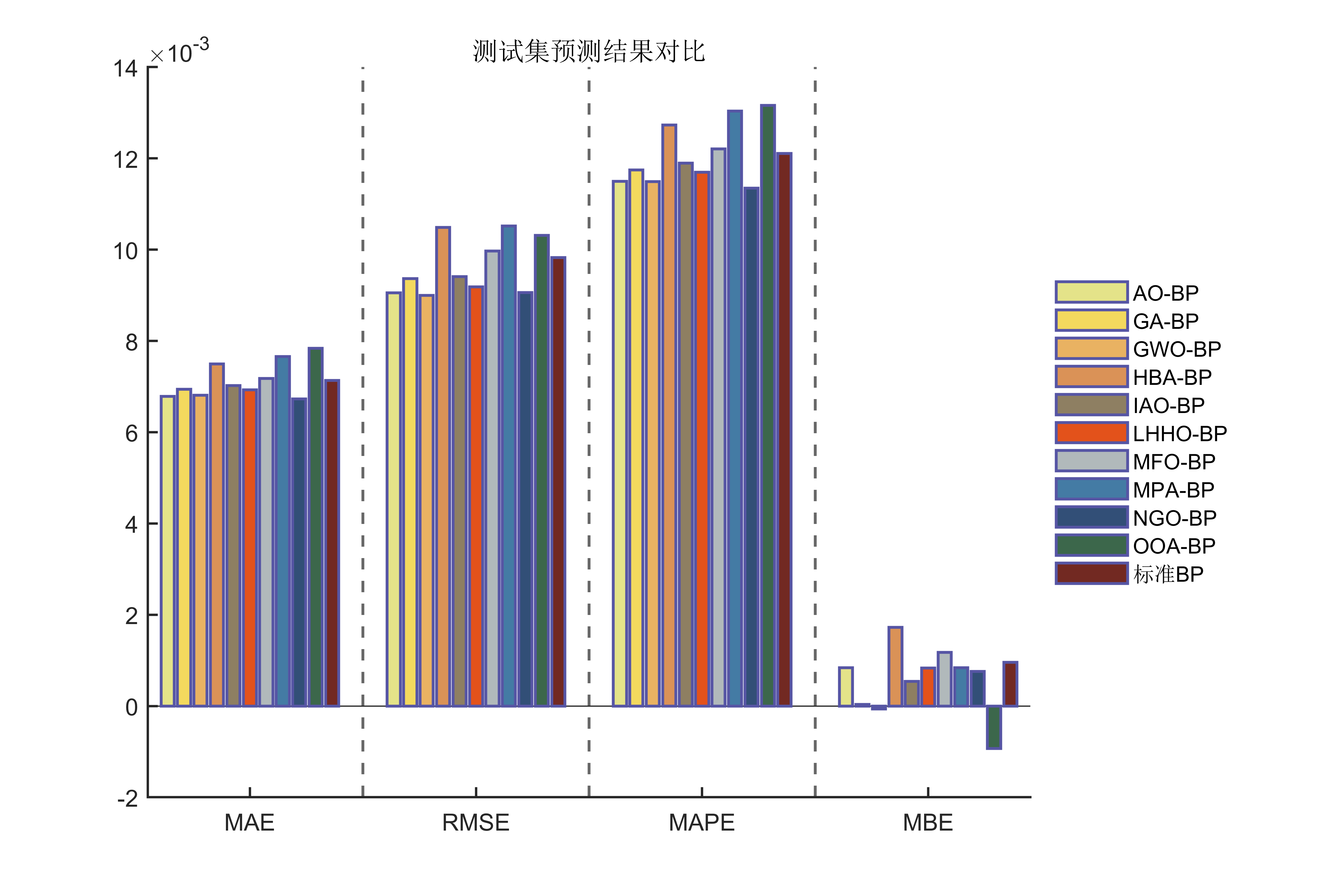
文章总览：YuanDaiMa2048博客文章总览

深度学习之激活函数

激活函数
- 基本概念
- 分类
- 常见的激活函数
- - 2. Tanh/双曲正切激活函数
  - 3. ReLU激活函数
  - 4. Softmax激活函数
- PyTorch中如何使用
- - 1. 线性激活函数
  - 2. 非线性激活函数
  - - Sigmoid
    - Tanh
    - ReLU
    - Leaky ReLU
    - Parametric ReLU (PReLU)
  - 使用激活函数

激活函数

基本概念

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。在神经元中，输入的input经过一系列加权求和后作用于另一个函数，这个函数就是这里的激活函数。类似于人类大脑中基于神经元的模型，激活函数最终决定了是否传递信号以及要发射给下一个神经元的内容。

常见的激活函数

Sigmoid函数
Sigmoid函数也被称为Logistic函数，通常用于神经网络的隐层神经元输出。其输出值的范围在 (0,1) 之间，因此可以将实数映射到 (0,1) 的区间，常用于二分类问题。在特征相差较复杂或差异不是特别大时，Sigmoid函数的效果较好。其数学表达式如下所示：
$\sigma(x) = \frac{1}{1 + e^{-x}}$

在这里插入图片描述

应用场景

用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适。
- 适用于二分类问题，输出范围为 (0,1)，可用于输出概率。
- 适用于多层网络中的中间层的非线性转换。

优点

输出范围在 (0,1) 内，适合作为概率输出。
函数是可微的，有助于梯度下降优化。
在输出接近 0 或 1 时，梯度较大，有助于参数更新。

缺点

Sigmoid 函数存在梯度消失问题，导致深层网络训练困难。
在输出远离中心位置时，梯度接近于 0，容易导致梯度消失。
Sigmoid 函数的计算相对复杂，会消耗更多的计算资源。

2. Tanh/双曲正切激活函数

Tanh函数，又称双曲正切激活函数（hyperbolic tangent activation function），与Sigmoid函数类似，但将其值范围压缩至 -1 到 1 的区间内。与Sigmoid函数不同的是，Tanh函数的输出以零为中心，因为其取值范围在 -1 到 1 之间。其数学表达式如下：
$\text{Tanh}(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

Tanh函数和Sigmoid函数之间存在一种简单的关系，可以通过Sigmoid函数的输出来表示Tanh函数。给定Sigmoid函数的输出 $σ (x)$ ，Tanh函数的输出可以表示为：
$\text{Tanh}(x) = 2σ(2x) - 1$
这个关系式表示了Tanh函数如何由Sigmoid函数的输出得出。

在这里插入图片描述

应用场景

适用于隐藏层的激活函数，可以将输入值映射到 (-1,1) 区间内。
适用于需要零中心化的场景，相较于 Sigmoid 函数，Tanh 函数的输出以 0 为中心。

优点

输出值在 (-1,1) 内，相比于 Sigmoid 函数，Tanh 函数的输出以 0 为中心，有助于神经网络的训练。
函数的形状对称，能够保持输入的符号信息。

缺点

仍然存在梯度消失问题，特别是在靠近饱和区域时。
计算复杂度较高，相比于 Sigmoid 函数，计算量大一些。

3. ReLU激活函数

ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题，在目前的深度神经网络中被广泛使用。ReLU函数本质上是一个斜坡（ramp）函数，其数学表达式如下：

这个函数的图像在 $x > 0$ 时是一条斜坡，斜率为1；在 $x < 0$ 时函数值为0。ReLU 函数可以表示为：

$\text{ReLU}(x) = \begin{cases} 0, & \text{if } x \leq 0 \\ x, & \text{if } x > 0 \end{cases} = \max(0, x)$

ReLU函数作为神经元的激活函数，在接收来自上一层神经网络的输入向量 $\mathbf{x}$ ，进行线性变换 $\mathbf{w}^T\mathbf{x} + b$ 之后，产生非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量 $\mathbf{x}$ ，使用ReLU函数的神经元会输出：

$\text{ReLU}(\mathbf{w}^T\mathbf{x} + b) = \max(0, \mathbf{w}^T\mathbf{x} + b)$

这个输出值将被传递至下一层神经元，或作为整个神经网络的输出（取决于神经元在网络结构中的位置）。

在这里插入图片描述

应用场景

在深度神经网络中广泛应用，能够有效避免梯度消失问题，加速网络的收敛速度。
许多成功的深度学习模型使用 ReLU 作为激活函数，如 AlexNet、VGG 等。

优点

相比于 Sigmoid 和 Tanh 函数，ReLU 函数的计算速度更快，因为它是简单的线性函数。
解决了梯度消失问题，能够在训练深层神经网络时更快地收敛。

缺点

Dead ReLU 问题：当输入为负时，ReLU 函数输出为 0，导致部分神经元失活，无法更新参数，影响模型性能。
对于负数部分，ReLU 函数的导数为 0，可能导致梯度消失问题。
不是零中心化，可能导致在训练过程中出现偏移。

Dead ReLU问题是指在训练神经网络时，ReLU激活函数所对应的神经元可能会因参数更新不当而“死亡”。具体来说，如果某个ReLU神经元在一次不恰当的参数更新后，对于所有的训练数据，其输出始终为负数，那么该神经元的参数梯度将永远为零，即无法被激活。这意味着，即使在后续的训练过程中，神经元接收到的输入值可能已经可以激活它，但由于参数梯度一直为零，该神经元也无法被激活。这种情况被称为“死亡ReLU问题”，可能出现在网络的任何隐藏层中。Dead ReLU问题可能会影响网络的性能和训练效果，因此在实践中需要采取措施来缓解这个问题，例如使用其他类型的激活函数或调整网络结构。

4. Softmax激活函数

Softmax函数是一种常用的激活函数，通常用于多分类问题中，将模型的原始输出转换为概率分布。Softmax函数接受一个包含任意实数的向量作为输入，并将每个元素的值转换为介于 0 和 1 之间的概率值，使得所有元素的概率之和等于 1。Softmax函数的数学表达式如下：
$\text{Softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}}$
其中， $\mathbf{z}$ 是输入向量， $N$ 是向量的维度， $\text{Softmax}(\mathbf{z})_i$ 表示 Softmax 函数的输出向量中的第 $i$ 个元素。

应用场景

用于多分类问题中，将模型的原始输出转换为类别概率分布。
在神经网络的输出层使用 Softmax 函数，可以得到每个类别的预测概率，然后根据概率进行分类决策。

优点

输出结果是一个概率分布，所有类别的概率之和为 1，便于理解和解释。
Softmax 函数是可微的，有助于梯度下降优化。
在训练过程中，Softmax 函数的梯度可以直接用于更新参数。

缺点

对于输入较大或较小的情况，Softmax 函数的输出会非常接近于 0 或 1，可能导致梯度消失问题。
Softmax 函数的计算量较大，因为要对所有元素进行指数运算和求和操作，特别是在处理大规模数据时，计算复杂度较高。

PyTorch中如何使用

在 PyTorch 中，可以使用 torch.nn 模块来定义各种激活函数。以下是几个经典激活函数的定义及其代码示例：

1. 线性激活函数

线性激活函数实际上是恒等函数，它可以通过直接返回输入实现：

import torch.nn as nn

class LinearActivation(nn.Module):
    def forward(self, x):
        return x

linear_activation = LinearActivation()

2. 非线性激活函数

Sigmoid

import torch.nn as nn

sigmoid = nn.Sigmoid()

Tanh

import torch.nn as nn

tanh = nn.Tanh()

ReLU

import torch.nn as nn

relu = nn.ReLU()

Leaky ReLU

import torch.nn as nn

leaky_relu = nn.LeakyReLU(negative_slope=0.01)  # negative_slope 参数用于控制负半轴的斜率

Parametric ReLU (PReLU)

import torch.nn as nn

prelu = nn.PReLU()  # PReLU 的参数可以通过设置 init 参数进行初始化

使用激活函数

可以在构建模型时将这些激活函数作为层添加到网络中。例如：

import torch
import torch.nn as nn

class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(10, 20)
        self.relu = nn.ReLU()  # 可以换成其他激活函数，如 nn.Sigmoid()
        self.fc2 = nn.Linear(20, 1)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

# 实例化模型
model = SimpleNet()