- 前言
- 一、相关参数设置
- 二、LSS算法前向过程
- 1.整体步骤
- 2.创建视锥
- 3.坐标变换
- 4.视锥点云特征
- 5.VoxelPooling
- 5.1 cumsum_trick(池化累积求和技巧):
- 5.2 VoxelPooling
- 总结
前言
目前在自动驾驶领域,比较火的一类研究方向是基于采集到的环视图像信息去构建BEV视角下的特征完成自动驾驶感知的相关任务。所以如何准确的完成从相机视角向BEV视角下的转变就变得由为重要。
目前感觉比较主流的方法可以大体分为2种:
1、显式估计图像的深度信息,完成BEV视角的构建,有文章也称其为自下而上的构建方式,代表作品有LSS、 BEVDet、BEVDepth等;
2、利用Transformer中的query查询机制(利用BEV Query构建BEV特征),这一过程也被称为自上而下的构建方式,代表作品有BEVFormer、PETR等;
LSS这篇论文的核心则是通过显式估计图像的深度信息,对采集到的环视图像进行特征提取,并根据估计出来的离散深度信息,实现图像特征向BEV特征的转换,进而完成自动驾驶中的语义分割任务。


一、相关参数设置
对于感知算法而言,比较重要的是要了解在BEV视角下,x轴和y轴方向的感知距离,以及BEV网格的单位大小。
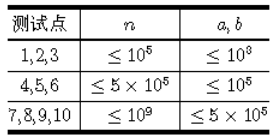
在自车周围俯视平面x-y方向划分n个网格,每个网格表示特定物理距离d m。如200×200的BEV网格,每格代表0.5m,这个网格就表示100m的平面范围。如果恰好自车中心在网格中心位置,那么网格就表示自车前、后和左、右各50m的范围。注意这里强调用网格划分平面空间,并不涉及网格内的特征。
在LSS源码中,其感知范围,BEV单元格大小,BEV下的网格尺寸如下:
1、感知范围
x轴方向的感知范围-50m~50m;y轴方向的感知范围-50m~50m;z轴方向的感知范围 -10m ~10m;
2、BEV单元格大小
x轴方向的单位长度 0.5m;y轴方向的单位长度 0.5m;z轴方向的单位长度20m;
3、BEV的网格尺寸
200 × 200 × 1;
4、深度估计范围
由于LSS需要显式估计像素的离散深度,论文给出的范围是 4m ~ 45m,间隔为1m,也就是算法会估计41个离散深度;

二、LSS算法前向过程
1.整体步骤
在进行详细描述LSS算法前向过程之前,先整体概括下LSS算法包括的5个步骤:
1、生成视锥,并根据相机内外参将视锥中的点投影到ego坐标系
需要注意的是,生成的锥点位置是基于图像坐标系,同时锥点是图像特征上每个单元格映射回原始图像的位置;一般分为两步来做,即视锥生成和锥点由图像坐标系向ego坐标系的坐标转换;
2、对环视图像完成特征提取,并构建图像特征点云
2.1、先利用Efficientnet-B0对环视图像进行特征提取(输入的环视图像 (bs,N,3,H,W),在进行特征提取之前,会将前两个维度进行合并提取特征,对应维度变换为 (bs,N,3,H,W) -> (bs*N,3,H,W));
2.2、对其中的后两层特征进行融合,丰富特征的语义信息,融合后的特征尺寸大小为 (bs*N,512,H /16,W/16);
2.3、估计深度方向的概率分布并输出特征图每个位置的语义特征 (用64维的特征表示),整个过程用1x1卷积层实现;
2.4、对2.3步骤估计出来的离散深度利用softmax函数计算深度方向的概率密度;
2.5、利用得到的深度方向的概率密度和语义特征通过外积运算构建图像特征点云。
3、利用变换后的ego坐标系的点和图像特征点云利用Voxel Pooling构建BEV特征;
4、对生成的BEV特征利用BEV Encoder做进一步的特征融合,然后对特征融合后的BEV特征进行语义分割;4.1、对BEV特征先利用ResNet-18进行多尺度特征提取;
4.2、对输出的多尺度特征进行特征融合 + 对融合后的特征实现BEV网格上的语义分割;
5、最后,将输出的语义分割结果与binimgs的真值做基于像素的交叉熵损失,从而指导模型的学习。
2.创建视锥
生成视锥,最后得到 D × H × W × 3的张量,这里的张量存储的是视锥点云坐标,也就是常见的(d,u,v)坐标。其中:
D的取值范围为:[ 4., 5., 6., 7., 8., 9., 10., 11., 12., 13., 14., 15., 16., 17., 18., 19., 20., 21., 22., 23., 24., 25., 26., 27., 28., 29., 30., 31., 32., 33., 34., 35., 36., 37., 38., 39., 40., 41., 42., 43., 44.],得到41个离散深度值;
H的取值范围为:[0.0000, 18.1429, 36.2857, 54.4286, 72.5714, 90.7143, 108.8571, 127.0000],在图像高度上8等分(16倍降采样);
W的取值范围为:[0.0000, 16.7143, 33.4286, 50.1429, 66.8571, 83.5714, 100.2857, 117.0000, 133.7143, 150.4286, 167.1429, 183.8571, 200.5714, 217.2857, 234.0000, 250.7143, 267.4286, 284.1429, 300.8571, 317.5714, 334.2857, 351.0000],在图像宽度上22等分(16倍降采样);
def create_frustum(self):
# 原始图片大小, ogfH:128 ogfW:352
ogfH, ogfW = self.data_aug_conf['final_dim']
# 下采样16倍后图像大小,fH: 8 fW: 22
fH, fW = ogfH // self.downsample, ogfW // self.downsample
# self.grid_conf['dbound'] = [4, 45, 1]
# 在深度方向上划分网格,ds:D×fH×fW (41*8*22)
ds = torch.arange(*self.grid_conf['dbound'], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)
D, _, _ = ds.shape # D:41 表示深度方向上网格的数量
# 在0到351上划分22个格子 xs:D×fH×fW (41×8×22)
xs = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(1, 1, fW).expand(D, fH, fW)
# 在0到127上划分8个格子 ys:D×fH×fW (41×8×22)
ys = torch.linspace(0, ogfH - 1, fH, dtype=torch.float).view(1, fH, 1).expand(D, fH, fW)
# D x H x W x 3
# 堆积起来形成网格坐标,frustum[i,j,k,0]就是(i,j)的位置
# 深度为k的像素的宽度方向上的栅格坐标frustum:D×fH×fW×3
frustum = torch.stack((xs, ys, ds), -1)
return nn.Parameter(frustum, requires_grad=False)
3.坐标变换
Get_Geometry():利用内外参,对N个相机视锥进行坐标变换,输出视锥点云在自车周围物理空间的位置索引;
对N个相机的视锥进行坐标变换,简单来说就是内外参以及6个视角的变换,输出结果是B×N×D×H×W×3,其中3是ego坐标系下的空间位置[x,y,z],B是batch_id,N是相机个数, D是深度分布数。
这样就等同于把ego周围空间划分为D×H×W块;
def get_geometry(self, rots, trans, intrins, post_rots, post_trans):
"""
rots:相机外参旋转, trans:相机外参平移, intrins:相机内参, post_rots:数据增强旋转, post_trans:数据增强平移
Determine the (x,y,z) locations (in the ego frame) of the points in the point cloud.
Returns B x N x D x H/downsample x W/downsample x 3
"""
B, N, _ = trans.shape # B: batch size N:环视相机个数
# undo post-transformation
# B x N x D x H x W x 3
# 抵消数据增强及预处理对像素的变化,即还原数据增强中旋转和平移对坐标的影响
points = self.frustum - post_trans.view(B, N, 1, 1, 1, 3)
points = torch.inverse(post_rots).view(B, N, 1, 1, 1, 3, 3).matmul(points.unsqueeze(-1))
# 图像坐标系 -> 归一化相机坐标系 -> 相机坐标系 -> 车身坐标系
# 但是自认为由于转换过程是线性的,所以反归一化是在图像坐标系完成的,然后再利用
# 求完逆的内参投影回相机坐标系
points = torch.cat((points[:, :, :, :, :, :2] * points[:, :, :, :, :, 2:3],
points[:, :, :, :, :, 2:3]
), 5) # 反归一化
combine = rots.matmul(torch.inverse(intrins))
points = combine.view(B, N, 1, 1, 1, 3, 3).matmul(points).squeeze(-1)
points += trans.view(B, N, 1, 1, 1, 3)
# (bs, N, depth, H, W, 3):其物理含义
# 每个batch中的每个环视相机图像特征点,其在不同深度下位置对应
# 在ego坐标系下的坐标
return points #维度不变,坐标值从相机坐标系->世界坐标系
4.视锥点云特征
观察下面的网格图,首先解释一下网格图的坐标,其中 α 代表某一个深度 softmax 概率(大小为H×W),c代表语义特征的某一个channel的特征图,那么 αc 就表示这两个矩阵的对应元素相乘,于是就为特征图的每一个点赋予了一个depth 概率,然后广播所有的 αc,就得到了不同的channel的语义特征在不同深度(channel)的特征图,经过训练,重要的特征颜色会越来越深(由于 softmax 概率高),反之就会越来越暗淡,趋近于0。

对原始图像进行逐个图像特征点地进行深度和语义的预测,输出视锥点云特征:
1、首先对原始图像通过EfficientNet学习特征;
2、然后一层卷积直接出D+C的维度,D属于深度分布,C是语义特征;
3、对D维深度做 softmax 归一化;
4、将D与C做外积;
5、最终输出的是H×W×D×C;
6、B×N张图像,对应的输出就是 B×N×H×W×D×C。
class CamEncode(nn.Module): # 提取图像特征,进行图像深度编码
def __init__(self, D, C, downsample):
super(CamEncode, self).__init__()
self.D = D # 41 深度区间【4-45】
self.C = C # 64 点的特征向量维度
# efficientnet 提取特征
self.trunk = EfficientNet.from_pretrained("efficientnet-b0")
self.up1 = Up(320+112, 512) # 上采样模块,输入320+112(多尺度融合),输出通道512
# 1x1卷积调整通道数,输出通道数为D+C,D为可选深度值个数,C为特征通道数
self.depthnet = nn.Conv2d(512, self.D + self.C, kernel_size=1, padding=0)
# 深度维计算softmax,得到每个像素不同深度的概率
def get_depth_dist(self, x, eps=1e-20):
return x.softmax(dim=1)
def get_depth_feat(self, x):
# 使用efficientnet提取主干网络特征 x: BN x 512 x 8 x 22
x = self.get_eff_depth(x)
# 1x1卷积变换维度,输出通道数为D+C,x: BN x 105(C+D) x 8 x 22
x = self.depthnet(x)
# softmax编码,理解为每个可选深度的权重
# 第二个维度的前D个作为深度维,进行softmax depth: BN x 41 x 8 x 22
depth = self.get_depth_dist(x[:, :self.D])
# 将深度概率分布和特征通道利用广播机制相乘
# 深度值 * 特征 = 2D特征转变为3D空间(俯视图)内的特征
new_x = depth.unsqueeze(1) * x[:, self.D:(self.D + self.C)].unsqueeze(2)
return depth, new_x # new_x: BN x 64 x 41 x 8 x 22
def get_eff_depth(self, x): # 使用efficientnet提取特征
# adapted from https://github.com/lukemelas/EfficientNet-PyTorch/blob/master/efficientnet_pytorch/model.py#L231
endpoints = dict()
# Stem
x = self.trunk._swish(self.trunk._bn0(self.trunk._conv_stem(x))) # x: BN x 32 x 64 x 176
prev_x = x
# Blocks
for idx, block in enumerate(self.trunk._blocks):
drop_connect_rate = self.trunk._global_params.drop_connect_rate
if drop_connect_rate:
drop_connect_rate *= float(idx) / len(self.trunk._blocks) # scale drop connect_rate
x = block(x, drop_connect_rate=drop_connect_rate)
if prev_x.size(2) > x.size(2):
endpoints['reduction_{}'.format(len(endpoints)+1)] = prev_x
prev_x = x
# Head
endpoints['reduction_{}'.format(len(endpoints)+1)] = x # x: BN x 320 x 4 x 11
x = self.up1(endpoints['reduction_5'], endpoints['reduction_4']) # 对endpoints[4]上采样,然后和endpoints[5] concat 在一起
return x # x: 24 x 512 x 8 x 22
def forward(self, x):
# depth: B*N x D x fH x fW(24 x 41 x 8 x 22) x: B*N x C x D x fH x fW(24 x 64 x 41 x 8 x 22)
depth, x = self.get_depth_feat(x)
return x
5.VoxelPooling
VoxelPooling():将上述Get_Geometry()和Cam_Encode()的输出作为输入,根据视锥点云在ego周围空间的位置索引,把点云特征分配到BEV pillar中,然后对同一个pillar中的点云特征进行sum-pooling处理,输出B,C,X,Y的BEV特征。
具体步骤如下:
1、首先将点云特征reshape成M×C,其中M=B×N×D×H×W;
2、然后将Get_Geometry()输出的空间点云转换到体素坐标下,得到对应的体素坐标。并通过范围参数过滤掉无用的点;
3、将体素坐标展平,reshape成一维的向量,然后对体素坐标中B、X、Y、Z的位置索引编码,然后对位置进行argsort,这样就把属于相同BEV pillar的体素放在相邻位置,得到点云在体素中的索引。
4、然后是一个神奇的操作,对每个体素中的点云特征进行sumpooling,代码中使用了cumsum_trick,巧妙地运用前缀和以及argsort的索引。输出是去重之后的Voxel特征,B×C×Z×X×Y。
5、最后使用unbind将Z维度切片,然后cat到C的维度上。代码中Z维度为1,实际效果就是去掉了Z维度,输出为B×C×X×Y的BEV 特征图。B×N张图像,对应的输出就是B×N×H×W×D×C;
5.1 cumsum_trick(池化累积求和技巧):
模型中使用Pillar累积求和池化,“累积求和”是通过bin id 对所有点进行排序,对所有特征执行累积求和,然后减去 bin 部分边界处的累积求和值来执行求和池化。无需依赖 autograd 通过所有3个步骤进行反向传播,而是可以导出整个模块的分析梯度,从而将训练速度提高 2 倍。
该层被称为“Frustum Pooling”,因为它将 n 个图像产生的截锥体转换为与摄像机数量 n 无关的固定维度 C×H×W 张量。
计算原理的过程示意图:

5.2 VoxelPooling
def voxel_pooling(self, geom_feats, x):
# geom_feats: B x N x D x H x W x 3 (4 x 6 x 41 x 8 x 22 x 3):在ego坐标系下的坐标点;
# x: B x N x D x fH x fW x C(4 x 6 x 41 x 8 x 22 x 64):图像点云特征
B, N, D, H, W, C = x.shape # B: 4 N: 6 D: 41 H: 8 W: 22 C: 64
Nprime = B*N*D*H*W # Nprime: 173184
# flatten x
x = x.reshape(Nprime, C) # 将特征点云展平,一共有 B*N*D*H*W 个点
# flatten indices
geom_feats = ((geom_feats - (self.bx - self.dx/2.)) / self.dx).long() # 将ego下的空间坐标[-50,50] [-10 10]的范围平移转换到体素坐标[0,100] [0,20],计算栅格坐标并取整
geom_feats = geom_feats.view(Nprime, 3) # 将体素坐标同样展平 geom_feats: B*N*D*H*W x 3 (173184 x 3)
batch_ix = torch.cat([torch.full([Nprime//B, 1], ix,
device=x.device, dtype=torch.long) for ix in range(B)]) # 每个点对应于哪个batch
geom_feats = torch.cat((geom_feats, batch_ix), 1) # geom_feats: B*N*D*H*W x 4(173184 x 4), geom_feats[:,3]表示batch_id
# filter out points that are outside box
# 过滤掉在边界线之外的点 x:0~199 y: 0~199 z: 0
kept = (geom_feats[:, 0] >= 0) & (geom_feats[:, 0] < self.nx[0])\
& (geom_feats[:, 1] >= 0) & (geom_feats[:, 1] < self.nx[1])\
& (geom_feats[:, 2] >= 0) & (geom_feats[:, 2] < self.nx[2])
x = x[kept] # x: 168648 x 64
geom_feats = geom_feats[kept]
# get tensors from the same voxel next to each other
ranks = geom_feats[:, 0] * (self.nx[1] * self.nx[2] * B)\
+ geom_feats[:, 1] * (self.nx[2] * B)\
+ geom_feats[:, 2] * B\
+ geom_feats[:, 3] # 给每一个点一个rank值,rank相等的点在同一个batch,并且在在同一个格子里面
sorts = ranks.argsort()
x, geom_feats, ranks = x[sorts], geom_feats[sorts], ranks[sorts] # 按照rank排序,这样rank相近的点就在一起了
# x: 168648 x 64 geom_feats: 168648 x 4 ranks: 168648
# cumsum trick
if not self.use_quickcumsum:
x, geom_feats = cumsum_trick(x, geom_feats, ranks)
else:
x, geom_feats = QuickCumsum.apply(x, geom_feats, ranks) # 一个batch的一个格子里只留一个点 x: 29072 x 64 geom_feats: 29072 x 4
# griddify (B x C x Z x X x Y)
final = torch.zeros((B, C, self.nx[2], self.nx[0], self.nx[1]), device=x.device) # final: 4 x 64 x 1 x 200 x 200
final[geom_feats[:, 3], :, geom_feats[:, 2], geom_feats[:, 0], geom_feats[:, 1]] = x # 将x按照栅格坐标放到final中
# collapse Z
final = torch.cat(final.unbind(dim=2), 1) # 消除掉z维
return final # final: 4 x 64 x 200 x 200
总结
LSS的优点:
1、LSS的方法提供了一个很好的融合到BEV视角下的方法。基于此方法,无论是动态目标检测,还是静态的道路结构认知,甚至是红绿灯检测,前车转向灯检测等等信息,都可以使用此方法提取到BEV特征下进行输出,极大地提高了自动驾驶感知框架的集成度。
2、虽然LSS提出的初衷是为了融合多视角相机的特征,为“纯视觉”模型而服务。但是在实际应用中,此套方法完全兼容其他传感器的特征融合。如果你想融合超声波雷达特征也不是不可以试试。
LSS的缺点:
1、极度依赖Depth信息的准确性,且必须显示地提供Depth 特征。当然,这是大部分纯视觉方法的硬伤。如果直接使用此方法通过梯度反传促进Depth网络的优化,如果Depth 网络设计的比较复杂,往往由于反传链过长使得Depth的优化方向比较模糊,难以取得较好效果。当然,一个好的解决方法是先预训练好一个较好的Depth权重,使得LSS过程中具有较为理想的Depth输出。
2、外积操作过于耗时。虽然对于机器学习来说,这样的计算量不足为道,但是对于要部署到车上的模型,当图片的feature size 较大, 且想要预测的Depth距离和精细度高时,外积这一操作带来的计算量则会大大增加。这十分不利于模型的轻量化部署,而这一点上,Transformer的方法反而还稍好一些。