大家好,欢迎来到无限大的频道。
今天和大家分享的是2552的题解思路。
题目描述:
统计上升四元组
一个长度为 n 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上升四元组的数目。
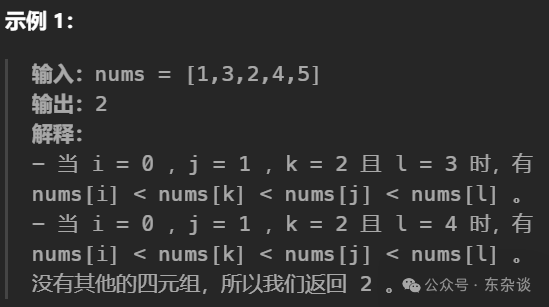
如果一个四元组 (i, j, k, l) 满足以下条件,我们称它是上升的:
- 0 <= i < j < k < l < n 且
- nums[i] < nums[k] < nums[j] < nums[l] 。

解题思路:
遇事不决,暴力解决。可以采用四层循环来暴力解决这个问题。对于每一个满足 i < j < k < l 的组合,我们都可以直接检查 nums[i] < nums[k] < nums[j] < nums[l] 是否成立。这种思路简单直观,但时间复杂度较高,为 O(n^4)。
为了在效率上有所提升,我们可以进行一部分预处理,减少一些不必要的计算。例如针对每个 nums[k] 和 nums[j] 的组合,检查前面的 i 和后面的 l。
优化思路:
我们可以使用如下步骤:
-
固定 j,用一个数组 lessThan 记录在此 j 之前比 nums[k] 小的个数。
-
固定 k 时,计算 nums[j] > nums[k] 情况下满足条件 nums[i] < nums[k] 的个数。
-
使用另一个数组 greaterThan 来统计在 k 之后比 nums[j] 大的 l 数量。
通过这个过程,我们可以将问题分解,并减少不必要的计算。
int countQuadruplets(int* nums, int numsSize) {
int ans = 0;
for (int j = 1; j < numsSize - 2; ++j) {
for (int k = j + 1; k < numsSize - 1; ++k) {
if (nums[j] < nums[k]) continue; // 需要满足 `nums[k] < nums[j]`
int lessThanK = 0; // 记录在 `j` 之前小于 `nums[k]` 的数量
for (int i = 0; i < j; ++i) {
if (nums[i] < nums[k]) {
++lessThanK;
}
}
int greaterThanJ = 0; // 记录在 `k` 之后大于 `nums[j]` 的 数量
for (int l = k + 1; l < numsSize; ++l) {
if (nums[l] > nums[j]) {
++greaterThanJ;
}
}
ans += lessThanK * greaterThanJ;
}
}
return ans;
}
代码解析:
-
外循环:固定 j,这样可以在 j 之前检查 i 的可能性。
-
内循环:固定 k,这里我们确保 j > k。
-
检查和计数:
-
lessThanK:在 j 之前找到所有小于 nums[k] 的数量。
-
greaterThanJ:在 k 之后找到所有大于 nums[j] 的数量。
-
-
累加结果:如果满足条件,使用 lessThanK * greaterThanJ 来累加有效的四元组数目。
此方法虽然仍然拥有三重循环,但通过减少某些不必要的检查,使时间复杂度降到 O(n^3),在可处理的范围内对于中等规模 n 的数组来说是可行的。