【数组与广义表】（基本概念与思路）

news2024/9/23 5:29:11

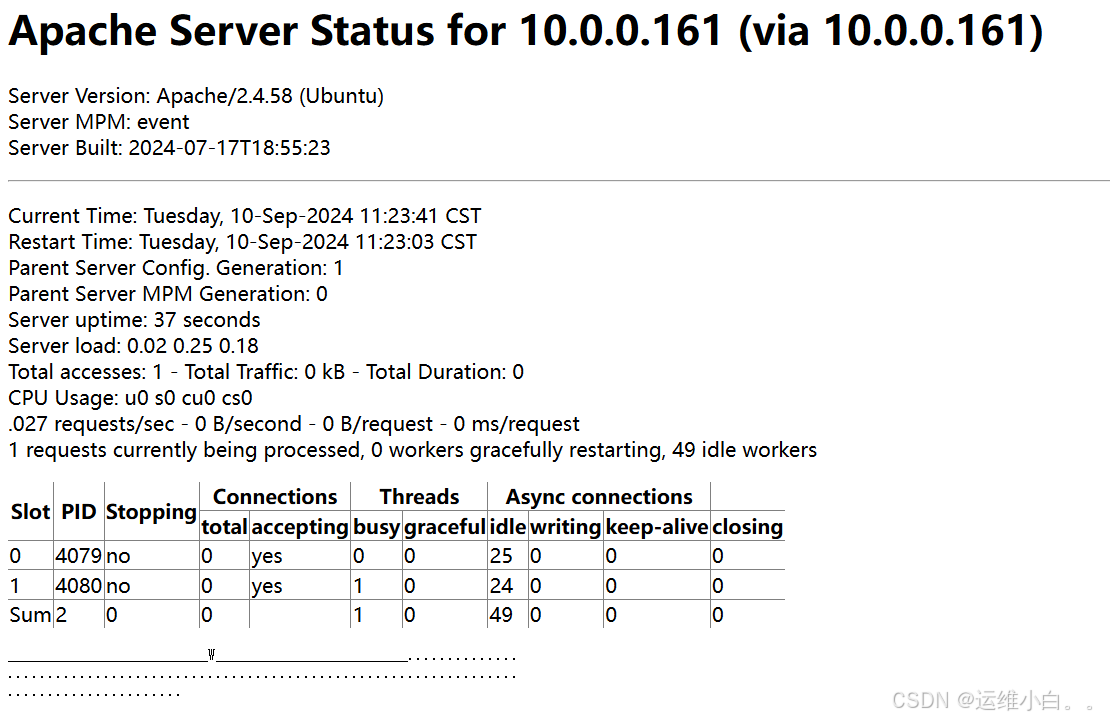
1.数组的定义及特点

数组：按一定格式排列起来的，具有相同类型的数据元素的集合。

1.1一维数组

  • 若线性表中的数据元素为非结构的简单元素，则称为一维数组。
  • 一维数组的逻辑结构:线性结构，定长的线性表
  • 声明格式:数据类型 变量名称 [长度];
  • 例:int num[5]={0，1，2，3，4};

1.2二维数组

  • 若一维数组中的数据元素又是一维数组结构，则称为二维数组。

  • 二维数组的逻辑结构：既可以看作线性结构，又可以看作非线性结构
    在这里插入图片描述

  • 声明格式:数据类型 变量名称[行数[[列数];

  • 其中，行数为第一维的长度，列数是第二维的长度

  • 例:int num[5][8];
    注意：在C语言中，一个二维数组类型也可以定义为一维数组类型
    (其分量类型为一维数组类型)，即：
    在这里插入图片描述
    1.typedef elemtype array2[m][n]; 这行代码定义了一个名为 array2 的新类型，它是一个二维数组，其元素类型为 elemtype，第一维大小为 m，第二维大小为 n。这意味着你可以使用 array2 来声明一个具有 m 行和 n 列的数组。
    2.typedef elemtype array1[n]; 这行代码定义了一个名为 array1 的新类型，它是一个一维数组，其元素类型为 elemtype，大小为 n。
    3.typedef array1 array2[m]; 这行代码实际上是将 array2 定义为一个指向 array1 类型数组的指针，这里的 m 表示指针可以指向 m 个 array1 类型的数组。换句话说，它创建了一个指向一维数组（每个一维数组有 n 个 elemtype 元素）的指针数组，每个指针指向一个 n 元素的数组。

m行n列：
在这里插入图片描述

如上图：

1.2.1 若看做线性结构，

我们可以把每一行看做一维数组中的一个元素（共m个元素）：
下标i表示一整行看做一个整体元素
在这里插入图片描述

也可以把每一列看做一维数组中的一个元素（共n个元素）：
在这里插入图片描述
下标j表示一整列看做一个整体元素

1.2.2 若看做非线性结构，

  • 以a11为例：
    在这里插入图片描述
  • 在所在行中有一个前驱，一个后继；
  • 在所在列中同样有一个前驱，一个后继
  • 即一个元素不只有一个前驱和一个后继了，即为不是一对一的非线性结构

1.3三维数组---------n维数组：

  • 若二维数组中的元素又是一个一维数组，则称作三维数组。
  • 若 n-1维数组中的元素又是一个一维数组结构，则称作 n维数组。

在这里插入图片描述

  • 数组基本操作:除了结构的初始化和销毁之外只有取元素和修改元素值的操作。

2.数组的抽象类型定义

在这里插入图片描述

2.1实例：

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

COL每一列间的前驱后继关系：如a00** 在列上的后继为 a10
ROW:每一行间的前驱后继关系：如a00 在行上的后继为 a01

3.数组的顺序存储

在这里插入图片描述
在这里插入图片描述

3.1一维数组实例;

在这里插入图片描述
在这里插入图片描述
这里的地址编号没有使用正规的16进制，是因为便于表述和计算
在这里插入图片描述

  • 需要知道的信息：第一个元素(下标为0)的起始地址a，每个元素占多大空间L，待计算地址元素之前共存在几个元素i
  • 则下标为i的元素的起始地址为：a+i*L
  • 所以这里LOC(3)=2000+3*4=2012

总结得到一维数组中元素起始地址的计算方法：
在这里插入图片描述

3.2二维数组

存储单元是一维结构，而数组是个多维结构,则用一组连续存储单元存放数组的数据元素就有个次序约定问题。

m行n列的二维数组

在这里插入图片描述
在这里插入图片描述

3.2.1行序为主序：C,PASCAL,JAVA, Basic

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
具体在内存中的存储：
在这里插入图片描述
在这里插入图片描述
m行n列的元素从头到尾，一行一行地存储在下标为0~m*n-1这个连续的内存空间中

3.2.1.1二维数组实例;

有二维数组A[m][n](A[0… …m-1][0… …n-1]),则如何计算数组元素a[i][j]的存储位置？

与一维数组类似：
在这里插入图片描述

  • 需要知道的信息：第一个元素(下标为0)的起始地址a，每个元素占多大空间L，待计算地址元素之前共存在几个元素i
  • 只不过这里待计算地址元素之前共存在几个元素i通过计算前面有几行元素，和该元素所处行中在该元素之前有几个元素来取得

在这里插入图片描述
分析过程如下：
在这里插入图片描述

3.2.2 列序为主序：FORTRAN

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
具体在内存中的存储：
在这里插入图片描述

在这里插入图片描述

m行n列的元素从头到尾，一列一列地存储在下标为0~m*n-1这个连续的内存空间中

3.3三维数组------n维数组（了解即可）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4.特殊矩阵的压缩存储（思路为重）

4.1为什么需要压缩存储

  • 矩阵: 一个由 m*n个元素排成的 m行n列的表
    在这里插入图片描述
  • 矩阵的常规存储: 将矩阵描述为一个二维数组。
  • 矩阵的常规存储的特点:
    （1）可以对其元素进行随机存取;
    （2）矩阵运算非常简单;
    （3）存储的密度为1。
  • 不适宜常规存储的矩阵:
    （1）值相同的元素很多且呈某种规律分布；
    （2）零元素多
  • 矩阵的压缩存储:
    （1）为多个相同的非零元素只分配一个存储空间;
    （2）对零元素不分配空间。
  • 能够压缩的矩阵类型：如对称矩阵，对角矩阵，三角矩阵，稀疏矩阵等

4.2对称矩阵的压缩存储

4.2.1特点与存储方法

在这里插入图片描述
这里的占用空间数，是使用等差数列求和公式：Sn=n*(an+a1)/2求解得到的

4.2.2对称矩阵的存储结构

  • 对称矩阵上下三角中的元素数均为:（注意是n行n列的矩阵）
    推理过程：
    第一行1个，第二行2个，…第n行n个：
    1+2+3+…+n= n*(an+a1)/2 = n*(n+1)/2
    在这里插入图片描述
  • 可以以行序为主序将元素存放在一个一维数组中。
    在这里插入图片描述
  • 例如:以行序为主序存储下三角:
    在这里插入图片描述
    在这里插入图片描述
    则aij的下标K为 (i-1)*i/2+(j-1)
    推导如下：
    在这里插入图片描述

4.3三角矩阵的存储结构

4.3.1特点与存储方法（与对称矩阵十分类似，只多了一个共享存储单元）

在这里插入图片描述
注意这里下标为0的存储空间中存储常数c；
下三角矩阵下标推导：
在这里插入图片描述
下三角矩阵推的有点费劲，以后有机会再推

4.4对角矩阵（带状矩阵）的存储结构

4.4.1特点与存储方法

在这里插入图片描述
注意：

  • 有几条对角线上的元素为非零元素，就称为几对角矩阵

在这里插入图片描述
存储在二维数组中

4.5稀疏矩阵的存储结构

4.5.1特点与存储方法

4.5.1.1存储特点：

在这里插入图片描述

4.5.1.2存储方法：

实例一：6行7列的（伪）稀疏矩阵如下：
在这里插入图片描述
在这里插入图片描述
则使用三元组法进行存储：（这里的行列号均从1开始记起）

（1）i：非零元素所处行号
（2）j：非零元素所处列号
（3）aij:非零元素的元素值

在这里插入图片描述

4.5.1.2.1存储方法1：三元组顺序表法（有序的双下标法）

在这里插入图片描述

  • 那么通过这样的三元组顺序表就可以轻松地得到对应的稀疏矩阵
    在这里插入图片描述
  • 三元组顺序表的优劣：
    （1）三元组顺序表又称有序的双下标法。
    （2）三元组顺序表的优点:非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算。
    （3）三元组顺序表的缺点:不能随机存取。若按行号存取某一行中的非零元，则需从头开始进行查找。
4.5.1.2.2存储方法2：三元组链式存储法（十字链表法）
  • 十字链表法的优点
    在这里插入图片描述
  • 十字链表法的存储特点
    在这里插入图片描述
    数据域存：行数，列数，元素值
    指针域包含两个指针，保证衔接正常

两个实际的例子如下：
在这里插入图片描述
在这里插入图片描述
为了方便查找，我们需要两个头指针数组：
即行的头指针数组（长度等于行数）以及列的头指针数组（长度等于列数）

5.广义表

5.1广义表的定义与组成

5.1.1广义表的定义

在这里插入图片描述
一个具体的实例如下：
在这里插入图片描述

5.1.2广义表的组成

在这里插入图片描述

  • 表头：
    在这里插入图片描述
    在这里插入图片描述
    注意：表头可以是一个原子，也可以是一个子表
  • 表尾：
    在这里插入图片描述
    在这里插入图片描述
    注意：表尾不是最后一个元素，而是一个子表。
    需要将除表头之外的所有元素包含在括号里

5.1.3一些具体的实例：

在这里插入图片描述
分析（3）：表尾为((b,c)）;
两个括号。
外层括号证明表尾是一个子表，内层括号证明表尾中只有一个元素

5.1广义表的性质

在这里插入图片描述
在这里插入图片描述

5.1广义表与线性表的区别

在这里插入图片描述

5.2广义表的基本运算

  • （1）求表头GetHead(L):非空广义表的第一个元素，可以是一个原子，也可以是一个子表
    -（2）求表尾GetTail(L):非空广义表除去表头元素以外其它元素所构成的表。表尾一定是一个表

实例如下：
在这里插入图片描述
注意：广义表不能使用数组存储，需要使用链表进行存储

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2122339.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

仪表板展示丨DataEase看中国：中国月饼行业消费趋势报告

仪表板展示丨DataEase看中国：中国月饼行业消费趋势报告

中秋节是中国最重要的传统节日之一，月饼是具有浓厚节日特色的传统美食。近年来，月饼市场呈现出诸多新趋势和消费特点。在本文中，我们使用DataEase开源BI工具（http://github.com/dataease）对中国月饼行业的消费趋势进行…
阅读更多...
敏捷开发方法例题

敏捷开发方法例题

答案：B 敏捷方法 特点 极限编程XP 4大价值观，5大原则，12个最佳实践 水晶法 认为每一个不同的项目都需要一套不同的策略，约定和方法论，认为人对软件质量有重要影响，因此随着项目质量和开发人员须知的提…
阅读更多...
洛谷 P7391 「TOCO Round 1」自适应 PVZ

洛谷 P7391 「TOCO Round 1」自适应 PVZ

原题链接t 题目来源于：洛谷 题目本质：贪心，排序，平衡树 题目思路：把僵尸出现时刻和走进房子时刻想成左端点和右端点，按照右端点从小到大排序。第二对于同样可以使用的豌豆射手，我们一定选择上…
阅读更多...
在 HKCR 新增项和值

在 HKCR 新增项和值

; 1. Win11 HKCR 根键默认是 System 所有, Win10 HKCR 根键默认是 Administrators 所有。 ; 2. 以 System、管理员 还是 普通用户 登录系统？ ; 在注册表里，操作 HKCR 行为与以上两项无关，都统一如下: ; 项 查权限所有者 当…
阅读更多...
QT5实现https的post请求(QNetworkAccessManager、QNetworkRequest和QNetworkReply)

QT5实现https的post请求(QNetworkAccessManager、QNetworkRequest和QNetworkReply)

QT5实现https的post请求 前言一、一定要有sslErrors处理1、问题经过2、代码示例 二、要利用抓包工具1、问题经过2、wireshark的使用3、利用wireshark查看服务器地址4、利用wireshark查看自己构建的请求报文 三、返回数据只能读一次1、问题描述2、部分代码 总结 前言 QNetworkA…
阅读更多...
单片机-STM32 看门狗（八）

单片机-STM32 看门狗（八）

目录 一、看门狗概念 1、定义： 二、单片机中的看门狗 1、功能描述： 2、看门狗设置部分 预分频寄存器(IWDG_PR) 3、窗口看门狗 特性： 4、看门狗配置： 一、看门狗概念 看门狗--定时器（不属于基本定时器、通用定…
阅读更多...
HTTP 协议和 APACHE 服务

HTTP 协议和 APACHE 服务

WEB 服务基础 Internet 因特网 因特网是 Internet 的中文译名 在 20 世纪 60 年代（冷战时期），美国国防部高等研究计划署（ARPA）出于军事上的目的，建立了 ARPA 网络，该网络由四个分布在不同地方…
阅读更多...
FreeRTOS基础入门——FreeRTOS互斥信号量（十六）

FreeRTOS基础入门——FreeRTOS互斥信号量（十六）

个人名片： 🎓作者简介：嵌入式领域优质创作者🌐个人主页：妄北y 📞个人QQ：2061314755 💌个人邮箱：[mailto:2061314755qq.com] 📱个人微信：Vir2025WB…
阅读更多...
本地部署Llama 3.1大模型

本地部署Llama 3.1大模型

Meta推出的Llama 3.1系列包括80亿、700亿、4050亿参数版本，上下文长度扩展至12.8万tokens，并增加了对八种语言的支持。 部署模型需要用到Ollama的一个工具，访问官方网站https://ollama.com 点击下载，选择下载你对应的操作系统下…
阅读更多...
opencv图像透视处理

opencv图像透视处理

引言 在图像处理与计算机视觉领域，透视变换（Perspective Transformation）是一种重要的图像校正技术，它允许我们根据图像中已知的四个点（通常是矩形的四个角）和目标位置的四个点，将图像从一个视…
阅读更多...
2024.9.10 作业

2024.9.10 作业

代码&#xff1a; /*******************************************/ 文件名&#xff1a;widget.h /*******************************************/ #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QLabel> #include <QTimeEdit> #includ…
阅读更多...
opencv学习：信用卡卡号识别

opencv学习：信用卡卡号识别

该代码用于从信用卡图像中自动识别和提取数字信息。该系统将识别信用卡类型&#xff0c;并输出信用卡上的数字序列。 1.创建命令行参数 数字模板 信用卡 # 创建命令行参数解析器 ap argparse.ArgumentParser() # 添加命令行参数 -i/--image&#xff0c;指定输入图像路径 ap.…
阅读更多...
破局DRG/DIP亏损，医院应该怎么做

破局DRG/DIP亏损，医院应该怎么做

DRG/DIP付费实施后&#xff0c;医院各临床科室可结合前期数据积累&#xff0c;根据DRG/DIP专科病组/病种四级手术占比与医疗收入占比之间的变化关系、建立DRG/DIP战略分布象限图&#xff0c;将病组分为优势病组&#xff08;病种&#xff09;、潜力病组&#xff08;病种&#xf…
阅读更多...
线程（Thread）

线程（Thread）

目录 线程&#xff08;Thread&#xff09; 线程的创建方式 实现方式 Runnable和Callable的区别 线程的命名和优先级 线程的六种状态 线程的插队 线程的中断 线程的让出 守护线程 设置线程为守护线程 sleep()和wait()的区别 线程的同步synchronized锁 语法格式 实现…
阅读更多...
在线动漫信息平台

在线动漫信息平台

你好呀&#xff0c;我是计算机学姐码农小野&#xff01;如果有相关需求&#xff0c;可以私信联系我。 开发语言&#xff1a;Java 数据库&#xff1a;MySQL 技术&#xff1a;Spring Boot框架 工具&#xff1a;IDEA/Eclipse、Navicat、Maven 系统展示 首页 会员后台 管理员…
阅读更多...
day-52 下一个排列

day-52 下一个排列

思路 从后向前遍历数组&#xff0c;把遍历过的元素加入一个有序链表&#xff0c;没变里一个元素判断链表中是否有元素大于当前遍历元素&#xff0c;如果有&#xff0c;把链表中大于当前遍历元素的元素集合中最小的那一个元素赋给当前元素&#xff0c;然后将链表中剩余元素依次赋…
阅读更多...
建造者模式builder

建造者模式builder

此篇为学习笔记&#xff0c;原文链接 https://refactoringguru.cn/design-patterns/builder 能够分步骤创建复杂对象。 该模式允许你使用相同的创建代码生成不同类型和形式的对象
阅读更多...
JavaWeb【day14】--（SpingBoot原理）

JavaWeb【day14】--（SpingBoot原理）

SpingBoot原理 在前面十多天的课程当中&#xff0c;我们学习的都是web开发的技术使用&#xff0c;都是面向应用层面的&#xff0c;我们学会了怎么样去用。而我们今天所要学习的是web后端开发的最后一个篇章springboot原理篇&#xff0c;主要偏向于底层原理。 我们今天的课程安…
阅读更多...
2-2 opencv实战进阶系列 多边形识别

2-2 opencv实战进阶系列 多边形识别

目录 一、不说废话&#xff0c;先上现象 二、前言 三、思路讲解 step1&#xff1a;用阈值编辑器对图像进行处理。 step2&#xff1a;应用阈值进行二值化 step3&#xff1a;轮廓查找 step4&#xff1a; 显示文字 四、完整代码贴出 五、现象展示 六、结语 一、不说废话&…
阅读更多...
在单向链表中找环

在单向链表中找环

在单向链表中找环也是有多种办法&#xff0c;不过快慢双指针方法是其中最为简洁的方法之一&#xff0c;接下来介绍这种方法。 首先两个指针都指向链表的头部&#xff0c;令一个指针一次走一步&#xff0c;另一个指针一次走两步&#xff0c;如果它们相遇了&#xff0c;证明有环…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023