在描述两个量之间的关系时,我们通常可以说特定的输入值对应于特定的输出值。例如,放大器具有输入电压和输出电压,这些电压与增益相关(在现实生活中增益是频率的函数而不是常数)。如果我们忽略饱和等非理想因素,V OUT始终等于增益乘以V IN。
然而,如果这种关系是滞后的,我们就不能说特定的输入值总是产生特定的输出值。相反,输入与输出的关系取决于系统的历史,如图 1 中的经典磁滞曲线所示。

通用磁滞曲线。
图 1.简单的磁滞曲线。
横轴是输入,纵轴是输出。如果您选择位于磁滞曲线封闭部分内的输入值,则相应的输出值是多少?这个问题没有明确的答案,如图 2 所示。

滞后曲线,曲线内包含输入值。 输出值不清楚。
图 2.滞后曲线包围的输入值。输出值是不确定的。
迟滞和相对运动
为了正确回答有关哪个输出值对应于给定输入值的问题,我们需要有关系统历史的附加信息。在这里, 《物理学词典》中的定义特别有用:在存在滞后现象的情况下,输入与输出的关系取决于输入相对于输出是增加还是减少。增加和减少意味着运动,运动——正如亚里士多德指出的——以时间为前提,随着时间的推移而发生的变化被记录为历史。
因此,说滞后系统的当前状态取决于系统的历史是一种广义的、技术性较低的说法,即滞后使输入-输出关系依赖于相对运动。如果当前输入相对于输出正在增加(图 3),我们可以使用向上箭头标记的曲线找到输出值;如果当前输入相对于输出正在减少(图 4),我们可以使用向下箭头标记的曲线找到输出值。
输入相对于输出增加的滞后曲线,如蓝色箭头所示。
图 3.输入相对于输出增加的滞后曲线。

输入相对于输出减少的磁滞曲线,如蓝色箭头所示。
图 4.输入相对于输出减小的磁滞曲线。
“数字”磁滞曲线
如果我们将上面所示的平滑磁滞曲线拉伸并折叠成理想化的矩形传递函数,我们会得到图 5。由于习惯了比较器电路中的开/关类型磁滞动作,我个人发现这种“数字”版本的磁滞曲线比我们之前研究的渐进过渡更直观。
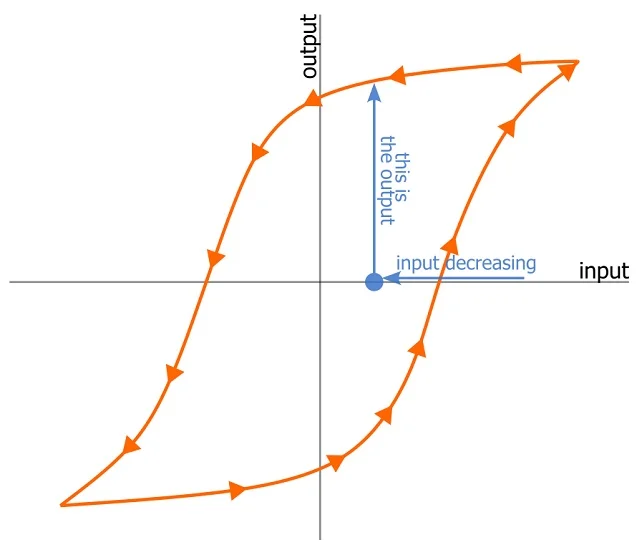
磁滞显示为矩形传递函数而不是曲线。
图 5.迟滞为矩形传递函数而不是曲线。
如果该电路没有迟滞,则传递函数将看起来像阶跃函数,并且只有一个阈值。如果输入位于该单个阈值的左侧,则输出将为逻辑低电平;如果它位于阈值右侧,则输出将为逻辑高电平。
当我们添加滞后时,我们创建了一个由两个不同阈值界定的不确定区域。如果输入值在正方形之外,则不存在不确定性:如果输入位于正方形左侧,则输出将为逻辑低电平;如果输入位于正方形右侧,则输出将为逻辑高电平。如果输入值位于正方形内的某个位置,则输出取决于系统的历史记录。
以下事件序列传达了由滞后创建的历史相关(或者,如果您愿意,相对运动相关)关系:
输入值低于阈值下限。输出为逻辑低电平。
输入越过下限并移入正方形。由于输入增加,输出不会改变。
输出保持逻辑低电平,直到输入达到较高阈值。然后输出转变为逻辑高电平。
输入增加到高于较高阈值。输出保持逻辑高电平。
输入开始减少并终达到较高的阈值。输出保持逻辑高电平。
输入现在位于正方形内部,但输出仍然为逻辑高电平。以前,输入位于正方形内部,输出为逻辑低电平。由于系统的历史,输出状态有所不同:以前输入位于正方形内且递增,但现在输入位于正方形内并递减。
输入达到下阈值。现在输出转换为逻辑低电平。