算法篇_RGB图像数据压缩与解压(单片机使用)

news2024/12/27 1:20:38

文章目录

  • 一、前言
  • 二、算法选型
    • 2.1 Run-Length Encoding (RLE)
    • 2.2 Differential Pulse-Code Modulation (DPCM)
  • 三、采用RLE算法实现图像压缩
  • 四、哈夫曼编码实现压缩和解压
    • 4.1 哈夫曼编码压缩自定义数据与还原
    • 4.2 哈夫曼编码压缩完成图像的压缩和还原

书接上回（上一篇文章已经讲解了如何封装BMP格式图片保存到本地SD卡）。

一、前言

在当今物联网(IoT)技术快速发展的背景下，嵌入式系统在各种应用场景中扮演着越来越重要的角色。随着物联网设备数量的不断增长，数据传输成为了关键的一环，尤其是在资源受限的环境中，如何高效地传输数据变得尤为重要。本文将介绍一个基于STM32F103ZET6微控制器的图像采集系统，该系统利用OV7725摄像头采集RGB565格式的图像，并通过MQTT协议将图像数据上传至阿里云物联网平台。 但是原始RGB565图像数据量巨大，直接传输会带来较高的网络负载，需要设计有效的压缩算法来减小数据体积。

考虑到单片机资源有限，无法使用第三方优秀的开源库，当前就基于Run-Length Encoding (RLE)无损压缩算法来减小图像数据的传输负担。RLE算法是一种简单有效的压缩方法，尤其适用于图像中存在大量连续重复像素值的情况。通过对重复像素的值和重复次数进行记录，可以显著减小图像数据的大小，从而降低网络传输的负载。下面会详细介绍RLE算法的设计与实现过程，以及如何在STM32F103ZET6微控制器上实现图像数据的压缩与解压，最终实现在阿里云物联网平台上进行高效的数据传输，并通过APP上位机进行图像数据的拉取与显示。

当前文章最重要的知识点是介绍： 数据的压缩和解压。

下面这个图是用的chargptAI自动生成的，不是实物图。
image-20240808155718461

二、算法选型

在单片机上进行图像数据压缩，需要选择是使用轻量级、简单但有效的压缩算法。

以下2个是可以用的压缩算法，适合在单片机上实现并能够有效减小数据量。

2.1 Run-Length Encoding (RLE)

RLE 是一种非常简单的无损压缩算法，特别适用于图像中有大量连续重复像素值的情况。通过记录重复像素的值和重复次数来实现压缩。

下面是算法的核心实现： 解压和压缩

#include <stdint.h>
#include <stdlib.h>
#include <stdio.h>

// RLE 压缩函数
size_t RLE_compress(const uint16_t *input, size_t length, uint8_t *output) {
    size_t out_index = 0;
    for (size_t i = 0; i < length; ) {
        uint16_t value = input[i];
        size_t run_length = 1;
        while (i + run_length < length && input[i + run_length] == value && run_length < 255) {
            run_length++;
        }
        output[out_index++] = (uint8_t)(run_length);
        output[out_index++] = (uint8_t)(value >> 8);
        output[out_index++] = (uint8_t)(value & 0xFF);
        i += run_length;
    }
    return out_index;
}

// RLE 解压函数
size_t RLE_decompress(const uint8_t *input, size_t length, uint16_t *output) {
    size_t out_index = 0;
    for (size_t i = 0; i < length; i += 3) {
        uint8_t run_length = input[i];
        uint16_t value = (input[i + 1] << 8) | input[i + 2];
        for (size_t j = 0; j < run_length; j++) {
            output[out_index++] = value;
        }
    }
    return out_index;
}

2.2 Differential Pulse-Code Modulation (DPCM)

DPCM 适用于图像中连续像素值变化较小的情况。通过记录相邻像素值的差值来实现压缩。

下面是算法的核心实现： 解压和压缩

#include <stdint.h>
#include <stdlib.h>
#include <stdio.h>

// DPCM 压缩函数
size_t DPCM_compress(const uint16_t *input, size_t length, int16_t *output) {
    output[0] = input[0];
    for (size_t i = 1; i < length; i++) {
        output[i] = input[i] - input[i - 1];
    }
    return length;
}

// DPCM 解压函数
size_t DPCM_decompress(const int16_t *input, size_t length, uint16_t *output) {
    output[0] = input[0];
    for (size_t i = 1; i < length; i++) {
        output[i] = output[i - 1] + input[i];
    }
    return length;
}

三、采用RLE算法实现图像压缩

下面这段代码采用Run-Length Encoding (RLE) 算法对 RGB565 格式图像数据进行压缩和解压。

代码里定义了一个常量数组 gImage_rgb565_100x100，存储 100x100 图像的 RGB565 像素数据（通过实际摄像头采集得到的）。

RLE 压缩函数 RLE_compress 遍历输入的 RGB565 数据数组，查找连续相同的像素值，并记录它们的长度和值，将这些信息存储到输出的压缩数组中。每次遇到一段连续的相同值时，它会记录该段的长度（最大为 255）和该像素值的高位和低位字节。压缩后的数据长度返回给调用者。解压函数 RLE_decompress 读取压缩后的数组，根据记录的长度和值还原原始数据，将这些值存储到输出的解压数组中。main 函数中，计算图像数据的长度，然后分配内存用于存储压缩和解压后的数据，分别调用压缩和解压函数进行处理。最后，打印出原始数据大小、压缩后的数据大小以及压缩率，以验证压缩效果。所有动态分配的内存最终被释放，以避免内存泄漏。通过这样的实现，可以在不使用第三方库的情况下，有效地减少图像数据的传输负荷，提高传输效率。

实现代码：

#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>

// RLE 压缩函数
size_t RLE_compress(const uint16_t* input, size_t length, uint8_t* output) {
    size_t out_index = 0;
    for (size_t i = 0; i < length; ) {
        uint16_t value = input[i];
        size_t run_length = 1;
        while (i + run_length < length && input[i + run_length] == value && run_length < 255) {
            run_length++;
        }
        output[out_index++] = (uint8_t)(run_length);
        output[out_index++] = (uint8_t)(value >> 8);
        output[out_index++] = (uint8_t)(value & 0xFF);
        i += run_length;
    }
    return out_index;
}

// RLE 解压函数
size_t RLE_decompress(const uint8_t* input, size_t length, uint16_t* output) {
    size_t out_index = 0;
    for (size_t i = 0; i < length; i += 3) {
        uint8_t run_length = input[i];
        uint16_t value = (input[i + 1] << 8) | input[i + 2];
        for (size_t j = 0; j < run_length; j++) {
            output[out_index++] = value;
        }
    }
    return out_index;
}

int main() {
    size_t length = sizeof(gImage_rgb565_100x100) / 2;
    uint16_t* rgb565_array = (uint16_t*)gImage_rgb565_100x100;

    // 分配 RLE 压缩后的数组
    uint8_t* rle_compressed = (uint8_t*)malloc(length * 3 * sizeof(uint8_t));
    if (rle_compressed == NULL) {
        perror("Unable to allocate memory for RLE compressed array");
        return 1;
    }

    // RLE 压缩
    size_t rle_compressed_length = RLE_compress(rgb565_array, length, rle_compressed);

    // 分配 RLE 解压后的数组
    uint16_t* rle_decompressed = (uint16_t*)malloc(length * sizeof(uint16_t));
    if (rle_decompressed == NULL) {
        perror("Unable to allocate memory for RLE decompressed array");
        return 1;
    }

    // RLE 解压
    size_t rle_decompressed_length = RLE_decompress(rle_compressed, rle_compressed_length, rle_decompressed);

    // 打印 RLE 压缩率
    printf("RLE 压缩算法:\n");
    printf("原始大小: %zu bytes\n", length * 2);
    printf("压缩后大小: %zu bytes\n", rle_compressed_length);
    printf("压缩比: %.2f%%\n", (double)rle_compressed_length / (length * 2) * 100);

    // 释放内存
    free(rle_compressed);
    free(rle_decompressed);

    return 0;
}

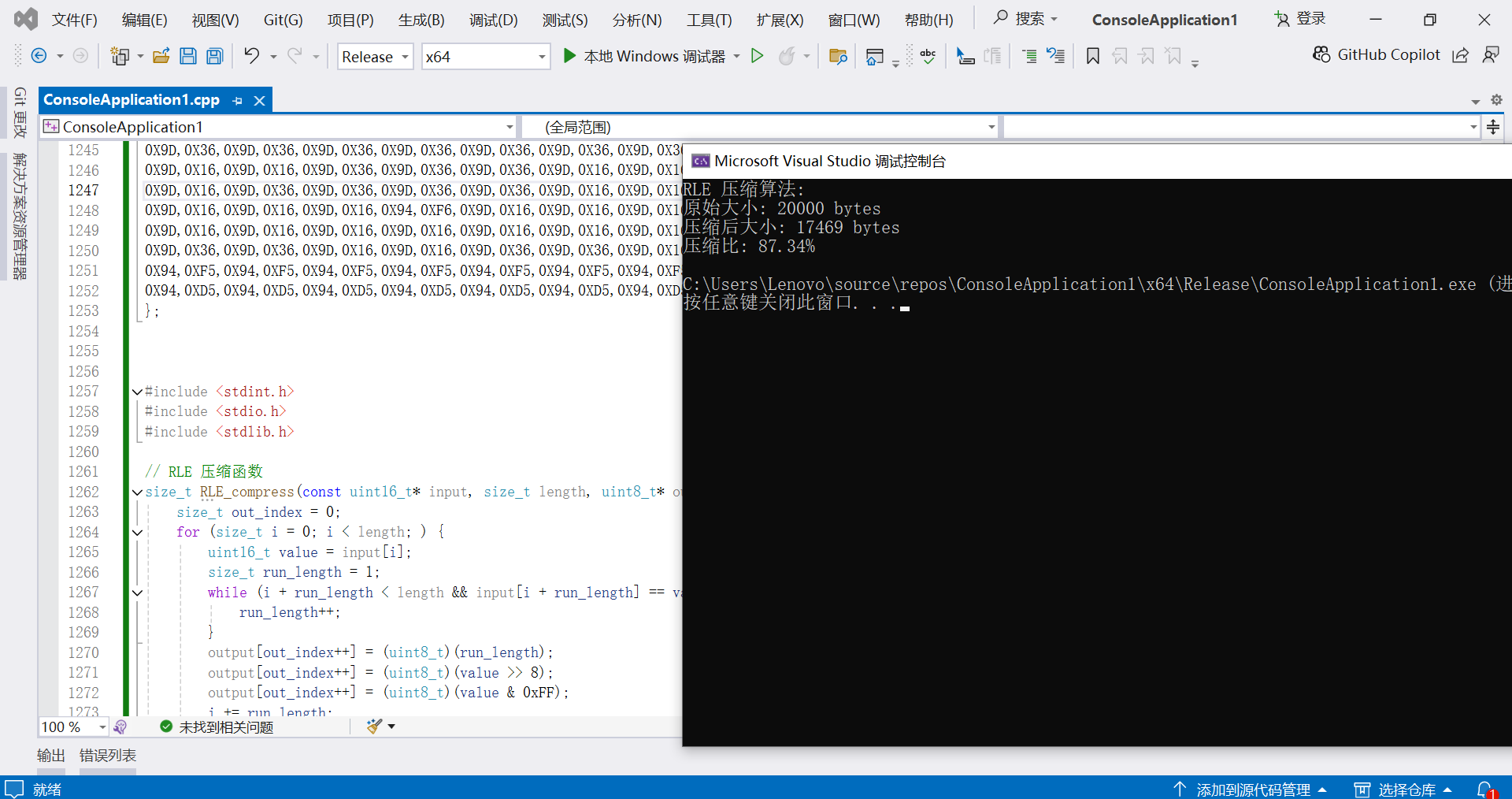
运行效果如下：

image-20240808151916619

四、哈夫曼编码实现压缩和解压

哈夫曼编码是一种常用的无损压缩算法，通过构建哈夫曼树，根据字符频率生成最优编码，从而实现数据压缩。

4.1 哈夫曼编码压缩自定义数据与还原

下面代码使用哈夫曼编码对一段自定义数据进行压缩和解压，并打印压缩前后的大小和压缩率，验证压缩效果。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 定义树节点结构
typedef struct Node {
    unsigned char ch;
    unsigned int freq;
    struct Node* left, * right;
} Node;

// 优先队列
typedef struct {
    Node** nodes;
    int size;
    int capacity;
} PriorityQueue;

PriorityQueue* createPriorityQueue(int capacity) {
    PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));
    pq->nodes = (Node**)malloc(capacity * sizeof(Node*));
    pq->size = 0;
    pq->capacity = capacity;
    return pq;
}

void swapNodes(Node** a, Node** b) {
    Node* t = *a;
    *a = *b;
    *b = t;
}

void heapify(PriorityQueue* pq, int idx) {
    int smallest = idx;
    int left = 2 * idx + 1;
    int right = 2 * idx + 2;
    if (left < pq->size && pq->nodes[left]->freq < pq->nodes[smallest]->freq) {
        smallest = left;
    }
    if (right < pq->size && pq->nodes[right]->freq < pq->nodes[smallest]->freq) {
        smallest = right;
    }
    if (smallest != idx) {
        swapNodes(&pq->nodes[smallest], &pq->nodes[idx]);
        heapify(pq, smallest);
    }
}

Node* extractMin(PriorityQueue* pq) {
    Node* temp = pq->nodes[0];
    pq->nodes[0] = pq->nodes[pq->size - 1];
    pq->size--;
    heapify(pq, 0);
    return temp;
}

void insertPriorityQueue(PriorityQueue* pq, Node* node) {
    pq->size++;
    int i = pq->size - 1;
    while (i && node->freq < pq->nodes[(i - 1) / 2]->freq) {
        pq->nodes[i] = pq->nodes[(i - 1) / 2];
        i = (i - 1) / 2;
    }
    pq->nodes[i] = node;
}

int isLeaf(Node* node) {
    return !(node->left) && !(node->right);
}

PriorityQueue* buildPriorityQueue(unsigned char data[], int freq[], int size) {
    PriorityQueue* pq = createPriorityQueue(size);
    for (int i = 0; i < size; ++i) {
        if (freq[data[i]] > 0) {
            Node* node = (Node*)malloc(sizeof(Node));
            node->ch = data[i];
            node->freq = freq[data[i]];
            node->left = node->right = NULL;
            pq->nodes[pq->size++] = node;
        }
    }
    for (int i = (pq->size - 1) / 2; i >= 0; --i) {
        heapify(pq, i);
    }
    return pq;
}

Node* buildHuffmanTree(unsigned char data[], int freq[], int size) {
    Node* left, * right, * top;
    PriorityQueue* pq = buildPriorityQueue(data, freq, size);
    while (pq->size != 1) {
        left = extractMin(pq);
        right = extractMin(pq);
        top = (Node*)malloc(sizeof(Node));
        top->ch = '\0';
        top->freq = left->freq + right->freq;
        top->left = left;
        top->right = right;
        insertPriorityQueue(pq, top);
    }
    return extractMin(pq);
}

void printCodes(Node* root, int arr[], int top, char** huffmanCodes) {
    if (root->left) {
        arr[top] = 0;
        printCodes(root->left, arr, top + 1, huffmanCodes);
    }
    if (root->right) {
        arr[top] = 1;
        printCodes(root->right, arr, top + 1, huffmanCodes);
    }
    if (isLeaf(root)) {
        huffmanCodes[root->ch] = (char*)malloc(top + 1);
        for (int i = 0; i < top; ++i) {
            huffmanCodes[root->ch][i] = '0' + arr[i];
        }
        huffmanCodes[root->ch][top] = '\0';
    }
}

char** buildHuffmanCodes(unsigned char data[], int freq[], int size) {
    Node* root = buildHuffmanTree(data, freq, size);
    int arr[100], top = 0;
    char** huffmanCodes = (char**)malloc(256 * sizeof(char*));
    for (int i = 0; i < 256; ++i) {
        huffmanCodes[i] = NULL;
    }
    printCodes(root, arr, top, huffmanCodes);
    return huffmanCodes;
}

void compress(unsigned char data[], int dataSize, char** huffmanCodes, unsigned char** compressedData, int* compressedSize) {
    int bitCount = 0;
    for (int i = 0; i < dataSize; ++i) {
        bitCount += strlen(huffmanCodes[data[i]]);
    }
    *compressedSize = (bitCount + 7) / 8;
    *compressedData = (unsigned char*)malloc(*compressedSize);
    memset(*compressedData, 0, *compressedSize);
    int byteIndex = 0, bitIndex = 0;
    for (int i = 0; i < dataSize; ++i) {
        char* code = huffmanCodes[data[i]];
        for (int j = 0; code[j] != '\0'; ++j) {
            if (code[j] == '1') {
                (*compressedData)[byteIndex] |= (1 << (7 - bitIndex));
            }
            bitIndex++;
            if (bitIndex == 8) {
                bitIndex = 0;
                byteIndex++;
            }
        }
    }
}

void decompress(unsigned char* compressedData, int compressedSize, Node* root, unsigned char** decompressedData, int dataSize) {
    *decompressedData = (unsigned char*)malloc(dataSize + 1);
    Node* current = root;
    int byteIndex = 0, bitIndex = 0;
    for (int i = 0; i < dataSize; ++i) {
        while (!isLeaf(current)) {
            if (compressedData[byteIndex] & (1 << (7 - bitIndex))) {
                current = current->right;
            }
            else {
                current = current->left;
            }
            bitIndex++;
            if (bitIndex == 8) {
                bitIndex = 0;
                byteIndex++;
            }
        }
        (*decompressedData)[i] = current->ch;
        current = root;
    }
    (*decompressedData)[dataSize] = '\0';
}

int main() {
    // 自定义数据
 	unsigned char data[] = "我是DS小龙哥 我正在测试这一段数据，看看能不能压缩成功";
 	int dataSize = strlen((char*)data);

    // 计算频率
    int freq[256] = { 0 };
    for (int i = 0; i < dataSize; ++i) {
        freq[data[i]]++;
    }

    // 构建哈夫曼编码
    char** huffmanCodes = buildHuffmanCodes(data, freq, 256);

    // 压缩
    unsigned char* compressedData;
    int compressedSize;
    compress(data, dataSize, huffmanCodes, &compressedData, &compressedSize);

    // 解压
    unsigned char* decompressedData;
    Node* root = buildHuffmanTree(data, freq, 256);
    decompress(compressedData, compressedSize, root, &decompressedData, dataSize);

    // 打印压缩前后的大小和压缩率
    printf("Original size: %d bytes\n", dataSize);
    printf("Compressed size: %d bytes\n", compressedSize);
    printf("Compression ratio: %.2f%%\n", (double)compressedSize / dataSize * 100);

    // 验证解压结果
    printf("Decompressed data: %s\n", decompressedData);

    // 释放内存
    free(compressedData);
    free(decompressedData);
    for (int i = 0; i < 256; ++i) {
        if (huffmanCodes[i]) {
            free(huffmanCodes[i]);
        }
    }
    free(huffmanCodes);

    return 0;
}

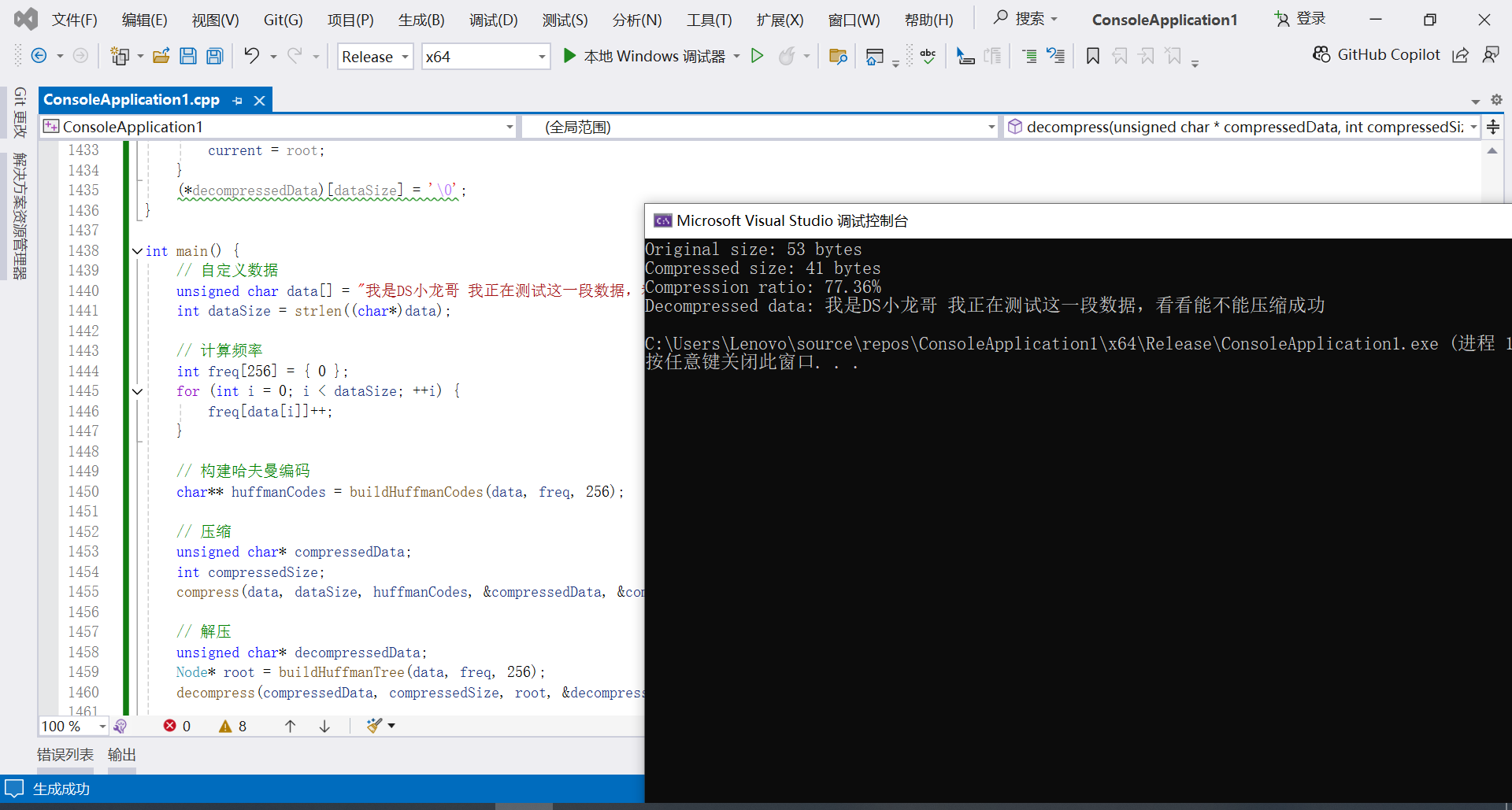
测试效果:

image-20240808154356035

4.2 哈夫曼编码压缩完成图像的压缩和还原

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 定义树节点结构
typedef struct Node {
    unsigned short ch; // 使用 unsigned short 表示 RGB565 数据
    unsigned int freq;
    struct Node* left, * right;
} Node;

// 优先队列
typedef struct {
    Node** nodes;
    int size;
    int capacity;
} PriorityQueue;

PriorityQueue* createPriorityQueue(int capacity) {
    PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));
    pq->nodes = (Node**)malloc(capacity * sizeof(Node*));
    pq->size = 0;
    pq->capacity = capacity;
    return pq;
}

void swapNodes(Node** a, Node** b) {
    Node* t = *a;
    *a = *b;
    *b = t;
}

void heapify(PriorityQueue* pq, int idx) {
    int smallest = idx;
    int left = 2 * idx + 1;
    int right = 2 * idx + 2;
    if (left < pq->size && pq->nodes[left]->freq < pq->nodes[smallest]->freq) {
        smallest = left;
    }
    if (right < pq->size && pq->nodes[right]->freq < pq->nodes[smallest]->freq) {
        smallest = right;
    }
    if (smallest != idx) {
        swapNodes(&pq->nodes[smallest], &pq->nodes[idx]);
        heapify(pq, smallest);
    }
}

Node* extractMin(PriorityQueue* pq) {
    Node* temp = pq->nodes[0];
    pq->nodes[0] = pq->nodes[pq->size - 1];
    pq->size--;
    heapify(pq, 0);
    return temp;
}

void insertPriorityQueue(PriorityQueue* pq, Node* node) {
    pq->size++;
    int i = pq->size - 1;
    while (i && node->freq < pq->nodes[(i - 1) / 2]->freq) {
        pq->nodes[i] = pq->nodes[(i - 1) / 2];
        i = (i - 1) / 2;
    }
    pq->nodes[i] = node;
}

int isLeaf(Node* node) {
    return !(node->left) && !(node->right);
}

PriorityQueue* buildPriorityQueue(unsigned short data[], int freq[], int size) {
    PriorityQueue* pq = createPriorityQueue(size);
    for (int i = 0; i < size; ++i) {
        if (freq[data[i]] > 0) {
            Node* node = (Node*)malloc(sizeof(Node));
            node->ch = data[i];
            node->freq = freq[data[i]];
            node->left = node->right = NULL;
            pq->nodes[pq->size++] = node;
        }
    }
    for (int i = (pq->size - 1) / 2; i >= 0; --i) {
        heapify(pq, i);
    }
    return pq;
}

Node* buildHuffmanTree(unsigned short data[], int freq[], int size) {
    Node* left, * right, * top;
    PriorityQueue* pq = buildPriorityQueue(data, freq, size);
    while (pq->size != 1) {
        left = extractMin(pq);
        right = extractMin(pq);
        top = (Node*)malloc(sizeof(Node));
        top->ch = 0;
        top->freq = left->freq + right->freq;
        top->left = left;
        top->right = right;
        insertPriorityQueue(pq, top);
    }
    return extractMin(pq);
}

void printCodes(Node* root, int arr[], int top, char** huffmanCodes) {
    if (root->left) {
        arr[top] = 0;
        printCodes(root->left, arr, top + 1, huffmanCodes);
    }
    if (root->right) {
        arr[top] = 1;
        printCodes(root->right, arr, top + 1, huffmanCodes);
    }
    if (isLeaf(root)) {
        huffmanCodes[root->ch] = (char*)malloc(top + 1);
        for (int i = 0; i < top; ++i) {
            huffmanCodes[root->ch][i] = '0' + arr[i];
        }
        huffmanCodes[root->ch][top] = '\0';
    }
}

char** buildHuffmanCodes(unsigned short data[], int freq[], int size) {
    Node* root = buildHuffmanTree(data, freq, size);
    int arr[100], top = 0;
    char** huffmanCodes = (char**)malloc(65536 * sizeof(char*)); // 65536 表示所有可能的 RGB565 值
    for (int i = 0; i < 65536; ++i) {
        huffmanCodes[i] = NULL;
    }
    printCodes(root, arr, top, huffmanCodes);
    return huffmanCodes;
}

void compress(unsigned short data[], int dataSize, char** huffmanCodes, unsigned char** compressedData, int* compressedSize) {
    int bitCount = 0;
    for (int i = 0; i < dataSize; ++i) {
        bitCount += strlen(huffmanCodes[data[i]]);
    }
    *compressedSize = (bitCount + 7) / 8;
    *compressedData = (unsigned char*)malloc(*compressedSize);
    memset(*compressedData, 0, *compressedSize);
    int byteIndex = 0, bitIndex = 0;
    for (int i = 0; i < dataSize; ++i) {
        char* code = huffmanCodes[data[i]];
        for (int j = 0; code[j] != '\0'; ++j) {
            if (code[j] == '1') {
                (*compressedData)[byteIndex] |= (1 << (7 - bitIndex));
            }
            bitIndex++;
            if (bitIndex == 8) {
                bitIndex = 0;
                byteIndex++;
            }
        }
    }
}

void decompress(unsigned char* compressedData, int compressedSize, Node* root, unsigned short** decompressedData, int dataSize) {
    *decompressedData = (unsigned short*)malloc(dataSize * sizeof(unsigned short));
    Node* current = root;
    int byteIndex = 0, bitIndex = 0;
    for (int i = 0; i < dataSize; ++i) {
        while (!isLeaf(current)) {
            if (compressedData[byteIndex] & (1 << (7 - bitIndex))) {
                current = current->right;
            }
            else {
                current = current->left;
            }
            bitIndex++;
            if (bitIndex == 8) {
                bitIndex = 0;
                byteIndex++;
            }
        }
        (*decompressedData)[i] = current->ch;
        current = root;
    }
}

int main() {
  
    int dataSize = sizeof(gImage_rgb565_100x100) / 2;
    unsigned short* data = (unsigned short*)gImage_rgb565_100x100;

    // 计算频率
    int freq[65536] = { 0 };
    for (int i = 0; i < dataSize; ++i) {
        freq[data[i]]++;
    }

    // 构建哈夫曼编码
    char** huffmanCodes = buildHuffmanCodes(data, freq, 65536);

    // 压缩
    unsigned char* compressedData;
    int compressedSize;
    compress(data, dataSize, huffmanCodes, &compressedData, &compressedSize);

    // 解压
    unsigned short* decompressedData;
    Node* root = buildHuffmanTree(data, freq, 65536);
    decompress(compressedData, compressedSize, root, &decompressedData, dataSize);

    // 打印压缩前后的大小和压缩率
    printf("Original size: %d bytes\n", dataSize * 2);
    printf("Compressed size: %d bytes\n", compressedSize);
    printf("Compression ratio: %.2f%%\n", ((double)compressedSize / (dataSize * 2)) * 100);

    // 验证解压结果（仅在开发时使用）
    for (int i = 0; i < dataSize; ++i) {
        if (data[i] != decompressedData[i]) {
            printf("Error: Decompressed data does not match original data at index %d.\n", i);
            break;
        }
    }

    // 释放内存
    free(compressedData);
    free(decompressedData);
    for (int i = 0; i < 65536; ++i) {
        if (huffmanCodes[i]) {
            free(huffmanCodes[i]);
        }
    }
    free(huffmanCodes);

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2120167.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java重修笔记 第五十一天 泛型

Java重修笔记 第五十一天 泛型

泛型 1. 对加入集合的数据类型进行约束&#xff0c;提高了安全性 2. 不用做专门的数据类型转换&#xff0c;就可以直接使用从集合取出来的对象&#xff0c;效率高 在类定义中使用泛型 1. 在类名后面跟上 <泛型列表> 表示该类所使用的使用泛型&#xff0c;具体是什么…
阅读更多...
nginx 使用篇 配置

nginx 使用篇 配置

一、介绍 1.介绍 Nginx是一个高性能的HTTP和反向代理服务器&#xff0c;同时也是一个邮件代理服务器&#xff0c;它以稳定性、丰富的功能集、简单的配置文件和低系统资源消耗而闻名。 作为一个轻量级的服务器&#xff0c;Nginx在处理高并发连接方面表现出色&#xff0c;能够支…
阅读更多...
怎么修复松下相机死机视频只有0字节（0KB）的MDT文件【实测可修复】

怎么修复松下相机死机视频只有0字节（0KB）的MDT文件【实测可修复】

死机后视频文件大小仅为0字节 松下S5相机录像死机&#xff0c;关机重新开机后有一个视频文件变成MDT&#xff0c;大小为0KB&#xff0c;录了30多分钟&#xff0c;本应为MOV格式的视频。0字节文件可以修复吗&#xff1f;怎么修复0字节的MDT文件为视频&#xff1f; 数据提取与视…
阅读更多...
认知杂谈55

认知杂谈55

今天分享 有人说的一段争议性的话 I I I I 内容摘要 这篇内容主要有以下要点&#xff1a;首先&#xff0c;人际交往有难度&#xff0c;要让大家都喜欢很难&#xff0c;需学习沟通技巧&#xff0c;可通过看书、关注抖音博主、参加培训班及看罗翔视频片段来提升。其次&#xf…
阅读更多...
【C++11 ——— 类的新功能】

【C++11 ——— 类的新功能】

C11 ——— 类的新功能 类的新功能默认成员函数类成员变量初始化强制生成默认函数的关键字default禁止生成默认函数的关键字delete 类的新功能 默认成员函数 原来C类中&#xff0c;有6个默认成员函数&#xff1a; 构造函数析构函数拷贝构造函数拷贝赋值重载取地址重载const …
阅读更多...
代码随想录刷题day27丨455.分发饼干 ,376. 摆动序列 ,53. 最大子序和

代码随想录刷题day27丨455.分发饼干 ,376. 摆动序列 ,53. 最大子序和

代码随想录刷题day27丨455.分发饼干 ,376. 摆动序列 ,53. 最大子序和 1.贪心算法理论基础 贪心的本质是选择每一阶段的局部最优&#xff0c;从而达到全局最优。 这么说有点抽象&#xff0c;来举一个例子&#xff1a; 例如&#xff0c;有一堆钞票&#xff0c;你可以拿走十张&a…
阅读更多...
论文《Graph Neural Networks with convolutional ARMA filters》笔记

论文《Graph Neural Networks with convolutional ARMA filters》笔记

【ARMA 2021 PAMI】本文介绍了一种新型的基于**自回归移动平均&#xff08;Auto-Regression Moving Average&#xff0c;ARMA&#xff09;**滤波器的图卷积层。与多项式滤波器相比&#xff0c;ARMA滤波器提供了更灵活的频率响应&#xff0c;对噪声更鲁棒&#xff0c;能更好地捕…
阅读更多...
【每日一题】LeetCode 104.二叉树的最大深度（树、深度优先搜索、广度优先搜索、二叉树）

【每日一题】LeetCode 104.二叉树的最大深度（树、深度优先搜索、广度优先搜索、二叉树）

【每日一题】LeetCode 104.二叉树的最大深度&#xff08;树、深度优先搜索、广度优先搜索、二叉树&#xff09; 题目描述 给定一个二叉树 root&#xff0c;我们需要计算并返回该二叉树的最大深度。二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。 思路分…
阅读更多...
Uni-app 开发鸿蒙 App 全攻略

Uni-app 开发鸿蒙 App 全攻略

一、开发前的准备工作 开发鸿蒙 App 之前&#xff0c;我们需要做好充分的准备工作。首先是工具的安装与配置。 Node.js 的安装&#xff1a;推荐使用 LTS 版本的 Node.js。可以前往 Node.js 的官方网站下载适合自己操作系统的安装包&#xff0c;如 Windows 用户根据自己的系统版…
阅读更多...
OpenHarmony鸿蒙开发（ Beta5.0）智能风扇设备开发实践

OpenHarmony鸿蒙开发（ Beta5.0）智能风扇设备开发实践

样例简介 智能风扇设备不仅可以接收数字管家应用下发的指令来控制风扇开启的时间&#xff0c;调节风扇挡位&#xff0c;更改风扇定时时间&#xff0c;而且还可以加入到数字管家的日程管理中。通过日程可以设定风扇相关的任务&#xff0c;使其在特定的时间段内&#xff0c;风扇…
阅读更多...
【MySQL】MySQL表的操作

【MySQL】MySQL表的操作

目录 创建表的语法创建表的示例查看表的结构进入数据库查看自己在哪个数据库查看自己所在数据库都有哪些表查看表的详细信息查看创建表时的详细信息 修改表修改表名修改表的内容插入几个数据增加一列修改一列的所有属性删除某一列修改列的名称 删除表 创建表的语法 CREATE TAB…
阅读更多...
DFS算法专题(二)——穷举vs暴搜vs深搜vs回溯vs剪枝【OF】决策树

DFS算法专题(二)——穷举vs暴搜vs深搜vs回溯vs剪枝【OF】决策树

目录 1、决策树 2、算法实战应用【leetcode】 2.1 题一&#xff1a;全排列 2.2.1 算法原理 2.2.2 算法代码 2.2 题二&#xff1a;子集 2.2.1 算法原理【策略一】 2.2.2 算法代码【策略一】 2.2.3 算法原理【策略二&#xff0c;推荐】 2.2.4 算法代码【策略二&#x…
阅读更多...
图像去噪技术：传统中值滤波与改进中值滤波算法的比较

图像去噪技术：传统中值滤波与改进中值滤波算法的比较

在数字图像处理中&#xff0c;去噪是一个至关重要的步骤&#xff0c;尤其是在图像受到椒盐噪声影响时。本文将介绍一种改进的中值滤波算法&#xff0c;并与传统的中值滤波算法进行比较&#xff0c;以展示其在去除椒盐噪声方面的有效性。 实验环境 软件&#xff1a;MATLAB图像…
阅读更多...
Centos如何配置阿里云的yum仓库作为yum源？

Centos如何配置阿里云的yum仓库作为yum源？

背景 Centos在国内访问官方yum源慢&#xff0c;可以用国内的yum源&#xff0c;本文以阿里云yum源为例说明。 快速命令 sudo mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.a…
阅读更多...
宏观学习笔记：GDP分析（二）

宏观学习笔记：GDP分析（二）

GDP分析&#xff08;一&#xff09;主要是介绍GDP相关的定义以及核算逻辑&#xff0c;本节主要介绍GDP的分析思路。GDP分析主要是2种方法&#xff1a;总量分析和结构分析。 1. 总量分析 1.1 数值选择 一般情况下&#xff0c;分析的对象都是 官方公布的GDP当季值。 1.2 趋势规…
阅读更多...
利用发电量和气象数据分析来判断光伏仿真系统的准确性

利用发电量和气象数据分析来判断光伏仿真系统的准确性

随着光伏产业的迅速发展&#xff0c;光伏仿真系统通过集成气象数据分析、发电量分析、投融资分析及损耗估算等功能&#xff0c;为光伏项目的全生命周期管理提供了科学依据。 光伏仿真系统集成了气象数据分析、发电量预测、投融资分析、损耗估算及光伏设计等功能。其中&#xf…
阅读更多...
qmt量化交易策略小白学习笔记第60期【qmt编程之期权数据--基于BS模型计算欧式期权隐含波动率--内置Python】

qmt量化交易策略小白学习笔记第60期【qmt编程之期权数据--基于BS模型计算欧式期权隐含波动率--内置Python】

qmt编程之获取期权数据 qmt更加详细的教程方法&#xff0c;会持续慢慢梳理。 也可找寻博主的历史文章&#xff0c;搜索关键词查看解决方案 &#xff01; 基于BS模型计算欧式期权隐含波动率 基于Black-Scholes-Merton模型,输入期权标的价格、期权行权价、期权现价、无风险利…
阅读更多...
【880高数】高等数学一刷错题整理

【880高数】高等数学一刷错题整理

第一章 函数、极限、连续 2024.8.11日 1. 2. 3. 4. 5. 2024.8.12日 1. 2. 3. 4. 5. 6. 7. 8. 2024.8.13日 1. 2. 3. 4. 2024.8.14日 1. 2. 3. 4. 5. 第二章 一元函数微分学及其应用 2024.8.15日 1. 2. 3. 4. 5. 6. 2024.8.16日 1. 2. 3. 4. 5. 2024.8.17日 1. 2. 3. 4…
阅读更多...
哈希表 和 算法

哈希表 和 算法

1.哈希表的作用&#xff1a;将我们要存储的数据&#xff0c;通过关键字与位置的关系函数&#xff0c;来确定具体的位置。 2.写哈希表时常出现的问题&#xff1a;哈希冲突/矛盾&#xff1a;当多个数据满足哈希函数的映射时出现 解决的方法为&#xff1a; 1&#xff09;开放地址…
阅读更多...
MVC设计模式与delegate

MVC设计模式与delegate

一、MVC MVC就是Model&#xff08;模型&#xff09;、View&#xff08;视图&#xff09;、Controller&#xff08;控制器&#xff09; 例如上面的 excel表&#xff0c; 数据、数据结构就是模型Model 根据数据形成的直观的、用户能直接看见的柱形图是视图View 数据构成的表格…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023