有营养的算法笔记（七）

news2024/11/21 1:45:18

字符串消除

1.题目描述

给定一个只由’a’和’b’组成的字符串str，str中"ab"和"ba"子串都可以消除，
消除之后剩下字符会重新靠在一起，继续出现可以消除的子串…你的任务是决定一种消除的顺序，最后让str消除到尽可能的短返回尽可能的短的剩余字符串。

2.解题思路

这个题目最容易想到的就是暴力解，对于暴力解我们的做法就是我遇到字符a和字符b我就试一下，尝试每个字符a和字符b相邻的情况下的答案那么最优的答案一定在其中。下面我们来看看这个代码如何来实现。

3.对应代码


	string Dispear1(const string& str)
	{
		int N = str.size();
		string ans=str;
		//所有情况我们都尝试一遍
		for (int i = 1; i < N; i++)
		{
			bool hasA = (str[i] == 'a' || str[i - 1] == 'b');
			bool hasB = (str[i] == 'b' || str[i - 1] == 'b');
			//判断相邻的两个字符是否是ab或者ba
			if (hasA && hasB) {
				//如果是那么我们就尝试把这个两个字符给删掉
				string cur = Dispear1(str.substr(0, i - 1) + str.substr(i + 1));
				//将[i-1,i]位置的字符给删掉
				if (cur.size() < ans.size()) {
					ans = cur;
				}
			}
		}
		return ans;
	}

上面这个代码非常的暴力，就是所有的情况我们全部都尝试一遍。不断的更新答案，够暴力哈哈哈哈。

4.方法二:贪心

方法二就是贪心，怎么贪了就是我遇到ab或者ba我就把它给消除掉。所以了我们可以使用一个栈，每次遍历到一个字符的时候我们就去栈里面看看这个栈里面的字符能否和我组成ba或者是ab如果能我们将栈里面的元素弹出即可。最后遍历栈里面的元素生成字符串返回即可，下面我们来看看如何来实现代码

	string Dispear2(const string& str)
	{
		int N = str.size();
		vector<int>stk(N);
		//使用数组来模拟栈
		int size = 0;
		//利用数组来实现栈
		for (int i = 0; i < N; i++)
		{
			//贪心遇到ab或者ba就消除
			bool hasA = size > 0 && str[stk[size - 1]] == 'a';
			bool hasB = size > 0 && str[stk[size - 1]] == 'b';
			hasA = hasA || (str[i] == 'a');
			hasB = hasB || (str[i] == 'b');
			//如果遇到了ab或者ba我们就将其消除即可
			if (hasB && hasA)
			{
				size--;
				//相当于弹出
			}
			else
			{
				stk[size++] = i;
			}

		}
		string ans;
		for (int i = 0; i < size; i++)
		{
			ans += str[stk[i]];
		}
		return ans;
	}
};

6.对应测试代码

#include<iostream>
#include<string>
#include<vector>
using namespace std;
//
//来自阿里
//给定一个只由'a'和'b'组成的字符串str，
//str中"ab"和"ba"子串都可以消除，
//消除之后剩下字符会重新靠在一起，继续出现可以消除的子串...
//你的任务是决定一种消除的顺序，最后让str消除到尽可能的短
//返回尽可能的短的剩余字符串

class Solution
{
public:
	//string Dispear1(const string& str)
	//{
	//	int N = str.size();
	//	string ans = str;
	//	for (int i = 1; i < N; i++)
	//	{
	//		bool hasA = (str[i] == 'a' || str[i - 1] == 'a');
	//		bool hasB = (str[i] == 'b' || str[i - 1] == 'b');
	//		//判断相邻的两个是否ab
	//		if (hasA && hasB) {
	//			string cur = Dispear1(str.substr(0, i - 1) + str.substr(i + 1));
	//			if (cur.size() < ans.size())
	//			{
	//				ans = move(cur);
	//			}
	//		}
	//	}
	//	return ans;
	//}

	string Dispear1(const string& str)
	{
		int N = str.size();
		string ans=str;
		//所有情况我们都尝试一遍
		for (int i = 1; i < N; i++)
		{
			bool hasA = (str[i] == 'a' || str[i - 1] == 'b');
			bool hasB = (str[i] == 'b' || str[i - 1] == 'b');
			//判断相邻的两个字符是否是ab或者ba
			if (hasA && hasB) {
				//如果是那么我们就尝试把这个两个字符给删掉
				string cur = Dispear1(str.substr(0, i - 1) + str.substr(i + 1));
				//将[i-1,i]位置的字符给删掉
				if (cur.size() < ans.size()) {
					ans = cur;
				}
			}
		}
		return ans;
	}

	string Dispear2(const string& str)
	{
		int N = str.size();
		vector<int>stk(N);
		//使用数组来模拟栈
		int size = 0;
		//利用数组来实现栈
		for (int i = 0; i < N; i++)
		{
			//贪心遇到ab或者ba就消除
			bool hasA = size > 0 && str[stk[size - 1]] == 'a';
			bool hasB = size > 0 && str[stk[size - 1]] == 'b';
			hasA = hasA || (str[i] == 'a');
			hasB = hasB || (str[i] == 'b');
			//如果遇到了ab或者ba我们就将其消除即可
			if (hasB && hasA)
			{
				size--;
				//相当于弹出
			}
			else
			{
				stk[size++] = i;
			}

		}
		string ans;
		for (int i = 0; i < size; i++)
		{
			ans += str[stk[i]];
		}
		return ans;
	}
};
string getRandomString(int v,int len)
{
	string ans;
	for (int i = 0; i < len; i++)
	{
		ans += (rand() % v + 'a');
	}
	return ans;
}
int main1()
{
	srand(time(0));
	int times = 1000;
	int v = 2;
	int len = 13;
	for (int i = 0; i < times; i++)
	{
		string str = getRandomString(v, len);
		string ans1 = Solution().Dispear1(str);
		string ans2 = Solution().Dispear2(str);
		if (ans1 != ans2)
		{
			cout << "错了" << endl;
			return 1;
		}
	}
	cout << "对了" << endl;
	return 0;
}

执行乘法的最大分数

1.对应letecode链接

执行乘法的最大分数

2.题目描述
在这里插入图片描述

3.解题思路

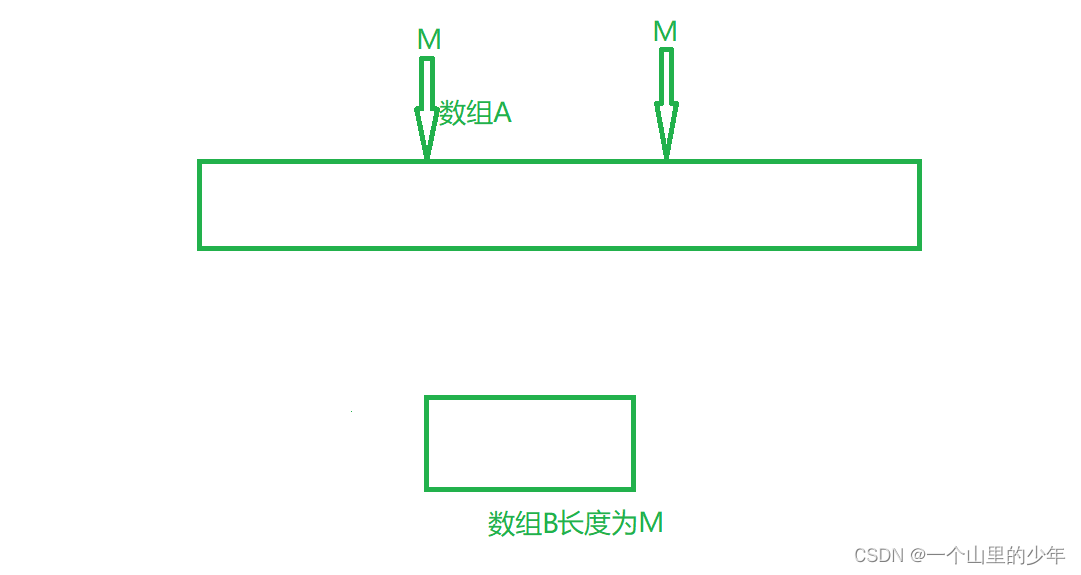
本题一看就是典型的范围上的尝试模型但是了这题有点坑让我细细道来，这题坑在那里了假设数组A的长度为N，数组B的长度为M。当N的长度大于2*M的时候那么中间这部分的数字是用不到的我们可以提前将其删除掉，不然我导致我们的时间复杂度非常的高。下面博主来画个图看看这种情况
在这里插入图片描述
由于每次我们只选择这个数组A的开头和结尾，那么最坏的情况下就是每次我都只选开头位置的数，或者每次只选择结尾位置的数。此时中间位置的数组我们可以直接删掉。这一步非常的重要这也就是这题坑的地方，下面的尝试就是非常的简单了，也就是数组A从[L…R]范围上每次可以选择开头或者结尾的数字和数组B当中的数字配对访问能够获得的最大得分。这就变得非常的简单了，不就是每次选择开头或者结尾吗？我都试一遍不就行了。但是数组B的小标我们是否也要传递一个参数进来了?其实是不需要的。我们完成可以通过A的左边界L和右边界R算出B数组的下标 ，如果A的左边界为L那么它左边消耗了L个数，如果A数组的右边界为R那么右边消耗了N-R-1个数把左边消耗的数和右边消耗的数加起来就是对应B数组的下标。下面我们来看看这个代码如何实现

class Solution {
  public:
    vector<vector<int>>dp;
    int maximumScore(vector<int>& nums, vector<int>& multipliers) {
        if (nums.size() < multipliers.size()) {
            return 0;
        }
        int N = nums.size();
        int M = multipliers.size();
        //中间部分肯定没用了
        if (N >= 2 * M) {
            int L = M;
            int R = N - M;
            while (R < N) {
                nums[L++] = nums[R++];
            }
            //将中间的数组移到后面去
            N = L;
            nums.erase(nums.begin() + L, nums.end());
            //把后面的东西全部删掉
        }
        dp.resize(N + 1, vector<int>(N + 1, INT_MAX));
        //缓存表

        return process(nums, multipliers, 0, nums.size() - 1);

    }

    int process(vector<int>& nums, vector<int>& mutil, int L, int R) {
        int len = L + (nums.size() - R - 1);
        //消耗数组的长度
        if (len >= mutil.size()) {
            return 0;
        }
        if (dp[L][R] != INT_MAX) {
            return dp[L][R];
        }


        int p1 = process(nums, mutil, L + 1, R) + nums[L] * mutil[len];
        int p2 = process(nums, mutil, L, R - 1) + nums[R] * mutil[len];
        //选择左边或者右边的数字和B数组进行配对
        dp[L][R] = max(p1, p2);
        return max(p1, p2);
    }
};

对应严格位置dp

class Solution {
  public:

    int maximumScore(vector<int>& nums, vector<int>& multipliers) {
        if (nums.size() < multipliers.size()) {
            return 0;
        }
        int N = nums.size();
        int M = multipliers.size();
        //中间部分肯定没用了
        if (N >= 2 * M) {
            int L = M;
            int R = N - M;
            while (R < N) {
                nums[L++] = nums[R++];
            }
            //将中间的数组移到后面去
            N = L;
            nums.erase(nums.begin() + L, nums.end());
            //把后面的东西全部删掉
        }

        vector<vector<int>>dp(N, vector<int>(N));

        for (int L = N - 1; L >= 0; L--) {
            for (int R = L; R < N; R++) {
                int len = L + N - R - 1;
                //注意这个可能会超过它的长度
                if (len >= multipliers.size()) {
                    dp[L][R] = 0;
                }

                else {
        int p1 = nums[L] * multipliers[len] + (L + 1 < N ? dp[L + 1][R] : 0);
      int p2 = nums[R] * multipliers[len] + (R - 1 >= 0 ? dp[L][R - 1] : 0);
                    dp[L][R] = max(p1, p2);
                }
            }
        }

        return dp[0][N - 1];
    }

返回最小路径和

1.题目描述

给定一个二维数组，其中全是非负数。 每一步都可以往上、下、左、右四个方向运动， 走过的路径，会沿途累加数字。 返回从左下角走到右下角的累加和最小的多少

2.解题思路

这题题了就是从左上点开始往四个方法我全部都试一遍，每个点都往四个方向试一遍，答案一定就在其中。在这里我们可以做一点优化什么优化了？就是这个二维数组的元素个数我们假设为MN个那么最优的解的步数一定不会超过MN-1因为不可能每个点都走一次，这样我们就可以省掉一个数组来记录一个点有没有被访问过了。下面我们来看看这个代码如何来写。

class Solution
{
public:
	vector<vector<int>>dxy{ {-1,0},{1,0},{0,1},{0,-1} };
	int bestWalk1(vector<vector<int>>& nums)
	{
		int M = nums.size();
		int N = nums[0].size() - 1;
		int step = M * N - 1;
		//最优解一定不会超过M*N-1步
		return process(nums, step, 0, 0, 0);
	}
	int process(vector<vector<int>>& map, int limit, int step, int row, int col)
	{
		if (row < 0 || col < 0 || row >= map.size() || col >= map[0].size()||step>=limit)
		{
			return INT_MAX;
		}
		if (row == map.size() - 1 && col == map[0].size() - 1) {
			return map[row][col];
		}
		int ans = INT_MAX;
		for (int i = 0; i < 4; i++)//四个方向我全部都产生一遍
		{
			int x = row + dxy[i][0];
			int y = col + dxy[i][1];
			int next = process(map, limit, step + 1, x, y);
			if (next != INT_MAX) {
				ans = min(ans, next + map[row][col]);
			}
		}
		
		return ans;

	}

方法一比较暴力，所有的可能性都尝试一遍虽然能够求得最终的结果但是这样的时间复杂度太高了。不太好，其实这题就是单源最短路径问题，一个点可以往四个方向走不就是这个点到另外四个点有边吗，所有我们只要判断这条边合法不合法就可以了，然后再使用单源最短路径当中的缔结特斯拉算法即可。这个算法博主再笔记二当中已经写过了在这里就不重复说明直接给出代码

//单源最短路径问题
	struct Node
	{
		Node(int r,int c,int p)
			:row(r),col(c),pathSum(p)
		{}
		int row;
		int col;
		int pathSum;//记录沿途路径的累加和
	};
	int bestWalk2(vector<vector<int>>& map)
	{
		int M = map.size();
		int N = map[0].size() ;
		vector<vector<bool>>visit(M, vector<bool>(N));
		auto cmp = [&](Node& a, Node& b) {return a.pathSum > b.pathSum; };
		priority_queue<Node, vector<Node>, decltype(cmp)>minHeap(cmp);
		//优先级队列
		
		minHeap.emplace(Node(0,0,map[0][0]));
		while (!minHeap.empty())
		{
			auto node = minHeap.top();
			minHeap.pop();
			int row = node.row;
			int col = node.col;
			if (visit[row][col]) {
				continue;
			}
			if (row == M - 1 && col == N - 1) {
				
				return node.pathSum;
			}
			//找到了这个点了
			visit[row][col] = true;
			for (int i = 0; i < 4; i++) {
				int x = row + dxy[i][0];
				int y = col + dxy[i][1];
				//往四个方向扩展
				if (x >= 0 && y >= 0 && x < M && y < N && !visit[x][y]) {
					minHeap.push(Node(x, y, node.pathSum + map[x][y]));
				}
			}

		}
		return INT_MAX;

	}

对应测试代码

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
// 来自学员问题
 //给定一个二维数组，其中全是非负数
 //每一步都可以往上、下、左、右四个方向运动
 //走过的路径，会沿途累加数字
 //返回从左下角走到右下角的累加和最小的多少
class Solution
{
public:
	vector<vector<int>>dxy{ {-1,0},{1,0},{0,1},{0,-1} };
	int bestWalk1(vector<vector<int>>& nums)
	{
		int M = nums.size();
		int N = nums[0].size() - 1;
		int step = M * N - 1;
		//最优解一定不会超过M*N-1步
		return process(nums, step, 0, 0, 0);
	}
	int process(vector<vector<int>>& map, int limit, int step, int row, int col)
	{
		if (row < 0 || col < 0 || row >= map.size() || col >= map[0].size()||step>=limit)
		{
			return INT_MAX;
		}
		if (row == map.size() - 1 && col == map[0].size() - 1) {
			return map[row][col];
		}
		int ans = INT_MAX;
		for (int i = 0; i < 4; i++)//四个方向我全部都产生一遍
		{
			int x = row + dxy[i][0];
			int y = col + dxy[i][1];
			int next = process(map, limit, step + 1, x, y);
			if (next != INT_MAX) {
				ans = min(ans, next + map[row][col]);
			}
		}
		
		return ans;

	}
	//单源最短路径问题
	struct Node
	{
		Node(int r,int c,int p)
			:row(r),col(c),pathSum(p)
		{}
		int row;
		int col;
		int pathSum;//记录沿途路径的累加和
	};
	int bestWalk2(vector<vector<int>>& map)
	{
		int M = map.size();
		int N = map[0].size() ;
		vector<vector<bool>>visit(M, vector<bool>(N));
		auto cmp = [&](Node& a, Node& b) {return a.pathSum > b.pathSum; };
		priority_queue<Node, vector<Node>, decltype(cmp)>minHeap(cmp);
		//优先级队列
		
		minHeap.emplace(Node(0,0,map[0][0]));
		while (!minHeap.empty())
		{
			auto node = minHeap.top();
			minHeap.pop();
			int row = node.row;
			int col = node.col;
			if (visit[row][col]) {
				continue;
			}
			if (row == M - 1 && col == N - 1) {
				
				return node.pathSum;
			}
			//找到了这个点了
			visit[row][col] = true;
			for (int i = 0; i < 4; i++) {
				int x = row + dxy[i][0];
				int y = col + dxy[i][1];
				//往四个方向扩展
				if (x >= 0 && y >= 0 && x < M && y < N && !visit[x][y]) {
					minHeap.push(Node(x, y, node.pathSum + map[x][y]));
				}
			}

		}
		return INT_MAX;

	}
};
vector<vector<int>>getRndomMap(int m, int n, int v)
{
	vector<vector<int>>map(m, vector<int>(n));
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			map[i][j] = rand() % v;
		}
	}
	return map;
}
int main()
{
	int times = 100;#include<iostream>
#include<vector>
#include<queue>
using namespace std;
// 来自学员问题
 //给定一个二维数组，其中全是非负数
 //每一步都可以往上、下、左、右四个方向运动
 //走过的路径，会沿途累加数字
 //返回从左下角走到右下角的累加和最小的多少
class Solution
{
public:
	vector<vector<int>>dxy{ {-1,0},{1,0},{0,1},{0,-1} };
	int bestWalk1(vector<vector<int>>& nums)
	{
		int M = nums.size();
		int N = nums[0].size() - 1;
		int step = M * N - 1;
		//最优解一定不会超过M*N-1步
		return process(nums, step, 0, 0, 0);
	}
	int process(vector<vector<int>>& map, int limit, int step, int row, int col)
	{
		if (row < 0 || col < 0 || row >= map.size() || col >= map[0].size()||step>=limit)
		{
			return INT_MAX;
		}
		if (row == map.size() - 1 && col == map[0].size() - 1) {
			return map[row][col];
		}
		int ans = INT_MAX;
		for (int i = 0; i < 4; i++)//四个方向我全部都产生一遍
		{
			int x = row + dxy[i][0];
			int y = col + dxy[i][1];
			int next = process(map, limit, step + 1, x, y);
			if (next != INT_MAX) {
				ans = min(ans, next + map[row][col]);
			}
		}
		
		return ans;

	}
	//单源最短路径问题
	struct Node
	{
		Node(int r,int c,int p)
			:row(r),col(c),pathSum(p)
		{}
		int row;
		int col;
		int pathSum;//记录沿途路径的累加和
	};
	int bestWalk2(vector<vector<int>>& map)
	{
		int M = map.size();
		int N = map[0].size() ;
		vector<vector<bool>>visit(M, vector<bool>(N));
		auto cmp = [&](Node& a, Node& b) {return a.pathSum > b.pathSum; };
		priority_queue<Node, vector<Node>, decltype(cmp)>minHeap(cmp);
		//优先级队列
		
		minHeap.emplace(Node(0,0,map[0][0]));
		while (!minHeap.empty())
		{
			auto node = minHeap.top();
			minHeap.pop();
			int row = node.row;
			int col = node.col;
			if (visit[row][col]) {
				continue;
			}
			if (row == M - 1 && col == N - 1) {
				
				return node.pathSum;
			}
			//找到了这个点了
			visit[row][col] = true;
			for (int i = 0; i < 4; i++) {
				int x = row + dxy[i][0];
				int y = col + dxy[i][1];
				//往四个方向扩展
				if (x >= 0 && y >= 0 && x < M && y < N && !visit[x][y]) {
					minHeap.push(Node(x, y, node.pathSum + map[x][y]));
				}
			}

		}
		return INT_MAX;

	}
};
vector<vector<int>>getRndomMap(int m, int n, int v)
{
	vector<vector<int>>map(m, vector<int>(n));
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			map[i][j] = rand() % v;
		}
	}
	return map;
}
int main()
{
	int times = 100;
	int m = 4;
	int n = 4;
	int val = 100;
	for (int i = 0; i < times; i++)
	{
		vector<vector<int>>map = getRndomMap(m, n, val);
		int ans1 = Solution().bestWalk1(map);
		int ans2 = Solution().bestWalk2(map);
		if (ans1 != ans2) {
			cout << "错了" << endl;
			return 1;
		}
	}
	cout << "对了" << endl;
	return 0;
}
	int m = 4;
	int n = 4;
	int val = 100;
	for (int i = 0; i < times; i++)
	{
		vector<vector<int>>map = getRndomMap(m, n, val);
		int ans1 = Solution().bestWalk1(map);
		int ans2 = Solution().bestWalk2(map);
		if (ans1 != ans2) {
			cout << "错了" << endl;
			return 1;
		}
	}
	cout << "对了" << endl;
	return 0;
}

猫鼠游戏问题

1.对应letecode链接

猫鼠游戏

2.题目描述

在这里插入图片描述

3.解题思路：
本题最暴力的方法就是进行暴力递归，尝试进行模拟。写一个递归函数确定猫和老鼠的位置，还要一个参数就是这是谁的回合，一张visit表记录某个状态如果某个状态如果某个状态重复出现那么一定是平局。轮到谁的回合就遍历所有的边看看自己能不能赢，如果能赢就可以直接返回了。下面我们来看看代码

4.对应代码

class Solution {
public:
    int catMouseGame(vector<vector<int>>& graph) {
             int N=graph.size();
             vector<vector<vector<bool>>>visit(N,vector<vector<bool>>(N,vector<bool>(2)));
             return process(graph,2,1,0,visit);

    }
    
int process(vector<vector<int>>&grap,int cat,int mouse,int turn,vector<vector<vector<bool>>>&visit)
    {
              //这个状态之前来过
              if(visit[cat][mouse][turn]){
                  return 0;
              }
              visit[cat][mouse][turn]=true;
              int ans=0;
              if(cat==mouse){
                  ans=2;
              }
              //老鼠赢了
              else if(mouse==0){
                  ans=1;
              }
              else
              {
                  //没赢
                   //老鼠的回合
                  if(turn==0){
                      ans=2;//最坏情况下是猫赢
                      for(int next:grap[mouse]){
                          int win=process(grap,cat,next,1,visit);
                          ans=(win==1?1:(win==0?0:ans));
                          if(ans==1){
                              break;
                          }
                      }
                  }
                  else
                  {
                          ans=1;
                          for(int next:grap[cat])
                          {
                              if(next==0){//注意猫不能去0位置
                                  continue;
                              }
                              //尝试没一条边看看自己能不能赢
                              int win=process(grap,next,mouse,0,visit);
                              ans=(win==2?2:(win==0?0:ans));
                              if(ans==2){
                                  break;
                              }
                          }

                  }

              }
            visit[cat][mouse][turn]=false;
            return ans;

    }

};

但是这样复杂度太高了，很多重复的过程我们需要重复计算。此时我们引入第二种做法这个改变这个turn的含义。在上面turn为0代表的是老鼠的回合，turn为1代表的是猫的回合.现在我们改变这个含义turn如果模2==1代表的是猫的回合，等于0代表的是老鼠的回合。下面此时我们就可以将使用一个dp表将每个状态记录了，下面我们来看看代码如何实现

class Solution {
  public:
    int catMouseGame(vector<vector<int>>& graph) {
        int N = graph.size();
        int limit = N * (N - 1) * 2 + 1;
        //不可能超过这个状态
        vector<vector<vector<int>>>visit(N + 1, vector<vector<int>>(N + 1,
                                         vector<int>(limit, -1)));
        return process(graph, 2, 1, 2, visit, limit);

    }

    int process(vector<vector<int>>& grap, int cat, int mouse, int turn,
                vector<vector<vector<int>>>& visit, int limit) {
        if (turn == limit) {
            return 0;
        }
        //这个状态之前来过
        if (visit[cat][mouse][turn] != -1) {
            return visit[cat][mouse][turn];
        }
        visit[cat][mouse][turn] = true;
        int ans = 0;
        if (cat == mouse) {
            ans = 2;
        }
        //老鼠赢了
        else if (mouse == 0) {
            ans = 1;
        } else {
            //没赢
            //老鼠的回合
            if (turn % 2 == 0) {
                ans = 2; //最坏情况下是猫赢
                for (int next : grap[mouse]) {
                    int win = process(grap, cat, next, turn + 1, visit, limit);
                    ans = (win == 1 ? 1 : (win == 0 ? 0 : ans));
                    if (ans == 1) {
                        break;
                    }
                }
            } else {
                ans = 1;
                for (int next : grap[cat]) {
                    if (next == 0) { //注意猫不能去0位置
                        continue;
                    }
                    int win = process(grap, next, mouse, turn + 1, visit, limit);
                    ans = (win == 2 ? 2 : (win == 0 ? 0 : ans));
                    if (ans == 2) {
                        break;
                    }
                }

            }

        }
        visit[cat][mouse][turn] = ans;
        return ans;

    }

};

在这里说明一下，假设有N个点那么猫有N*(N-1)种状态，同样的老鼠也有N*(N-1)种状态。最多也只有这个2*(N-1)*N种状态如果超过了这么多状态那么一定就是平局。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/212.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

（附源码）计算机毕业设计SSM基于人脸识别和测温的宿舍管理系统

（附源码）计算机毕业设计SSM基于人脸识别和测温的宿舍管理系统

&#xff08;附源码&#xff09;计算机毕业设计SSM基于人脸识别和测温的宿舍管理系统 项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09…
阅读更多...
Redis 集群安装-Centos

Redis 集群安装-Centos

Redis 集群安装-Centos Redis3.0以后的版本虽然有了集群功能&#xff0c;提供了比之前版本的哨兵模式更高的性能与可用性&#xff0c;但是集群的水平扩展却比较麻烦&#xff0c;今天就来带大家看看redis高可用集群如何做水平扩展&#xff0c;原始集群(见下图)由6个节点组成&am…
阅读更多...
【图灵MySQL】MySQL索引优化实战（上）

【图灵MySQL】MySQL索引优化实战（上）

【图灵MySQL】MySQL索引优化实战&#xff08;上&#xff09; 数据准备-SQL CREATE TABLE employees (id int(11) NOT NULL AUTO_INCREMENT,name varchar(24) NOT NULL DEFAULT COMMENT 姓名,age int(11) NOT NULL DEFAULT 0 COMMENT 年龄,position varchar(20) NOT NULL DEF…
阅读更多...
1024程序员节带你玩转图片Exif信息获取之JavaScript

1024程序员节带你玩转图片Exif信息获取之JavaScript

目录 一、前言 二、背景 三、Exif.js 1、Exif.js 简介 2、Exif.js 引入 四、多场景展示数据获取 1、原始图片直接获取 2、base64 编码文件加载 3、文件上传的方式加载 五、总结 一、前言 1024是2的十次方&#xff0c;二进制计数的基本计量单位之一。1G1024M&#xff0c;而…
阅读更多...
git工具基本操作命令

git工具基本操作命令

初始化 首先在某个文件下新建一个项目。然后使用git初始化命令开始正式管理写好的代码。 首先新建一个项目&#xff1a; 然后在上述文件夹中右键选择git&#xff0c;或者直接在该文件路径下打开cmd进行操作&#xff1a; 上述操作出现了.git文件夹&#xff0c;今后所有的操作都…
阅读更多...
Sharding-JDBC实现读写分离

Sharding-JDBC实现读写分离

前言 快一个月没有更新文章了&#xff0c;太忙了太忙了&#xff0c;虽然慢了一点&#xff0c;但是我肯定不会断更。上一篇文章是《Mysql主从复制》&#xff0c;光是数据库层面的主从复制可不行&#xff0c;应用层面也是需要读写分离的&#xff0c;所以接上一篇文章我们来讲如何…
阅读更多...
赶紧进来看看---万字博客详解C/C++中的动态内存管理

赶紧进来看看---万字博客详解C/C++中的动态内存管理

本篇博客主要介绍了C/C程序内部的内存开辟.动态内存分布 动态内存函数malloc calloc realloc free的使用 常见的动态内存错误.以及柔性数组的概念与使用 学会动态内存管理将不再局限于使用静态的空间,对内存空间的理解和使用将更进一层楼~ C/C动态内存管理一.认识C/C程序的内存…
阅读更多...
【C++升级之路】类与对象（中）

【C++升级之路】类与对象（中）

&#x1f31f;hello&#xff0c;各位读者大大们你们好呀&#x1f31f; &#x1f36d;&#x1f36d;系列专栏&#xff1a;【C学习与应用】 ✒️✒️本篇内容&#xff1a;类与对象知识汇总&#xff0c;包括6大默认成员函数、日期类的实现 &#x1f6a2;&#x1f6a2;作者简介&…
阅读更多...
graphQL入门分享

graphQL入门分享

是什么 一种用于 API 的查询语言&#xff1b;它与特定技术无关&#xff0c;你可以用任何语言实现它 简单理解&#xff0c;他能提供一个接口&#xff0c;让我们来调用&#xff0c;只是返回的数据格式更多是由我们前端来控制 为什么 官网&#xff1a;https://graphql.cn/ 1.请求你…
阅读更多...
深入理解计算机系统前篇总结

深入理解计算机系统前篇总结

&#x1f343;博主昵称&#xff1a;一拳必胜客 博主主页面链接&#xff1a;博主主页传送门 博主专栏页面连接&#xff1a;专栏传送门–计算机考研 &#x1f351;创作初心&#xff1a;本博客的初心是每天分享记录自己学习的脚步&#xff0c;和各位技术友探讨交流&#xff0c;同时…
阅读更多...
惠州龙门大米飘香 国稻种芯-中国水稻节：广东乡村振兴样板

惠州龙门大米飘香 国稻种芯-中国水稻节：广东乡村振兴样板

惠州龙门大米飘香 国稻种芯-中国水稻节&#xff1a;广东乡村振兴样板 人民日报客户端 新闻中国采编网 中国新闻采编网 谋定研究中国智库网 中国农民丰收节国际贸易促进会 国稻种芯中国水稻节 中国三农智库网-功能性农业农业大健康大会报道&#xff1a; 粒粒“龙门大米”精美飘…
阅读更多...
百度地图API的使用(附案例)

百度地图API的使用(附案例)

文章目录JavaScript API GL一、申请秘钥Hello World显示地址案例定位功能步行导航搜索功能地铁路线规划JavaScript API GL 百度地图JavaScript API是一套由JavaScript语言编写的应用程序接口&#xff0c;可帮助您在网站中构建功能丰富、交互性强的地图应用&#xff0c;支持PC端…
阅读更多...
经典文献阅读之--用于自动驾驶的高清地图生成技术

经典文献阅读之--用于自动驾驶的高清地图生成技术

0. 简介 这篇文章我们介绍一下论文“High-Definition Map Generation Technologies For Autonomous Driving: A Review“&#xff0c;2022年6月11日&#xff0c;来自加拿大Ontario Tech University。相较于网上的其他文章&#xff0c;本文更在意向读者更轻松全面的了解文章中介…
阅读更多...
【Web前端大作业】基于HTML+CSS+JavaScript制作西北大学新闻网站（7页）

【Web前端大作业】基于HTML+CSS+JavaScript制作西北大学新闻网站（7页）

&#x1f389;精彩专栏推荐 &#x1f4ad;文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业&#xff1a; 【&#x1f4da;毕设项目精品实战案例 (10…
阅读更多...
悬浮坐标解决方案：如何在图片获取xy鼠标位置和增加标注信息

悬浮坐标解决方案：如何在图片获取xy鼠标位置和增加标注信息

悬浮坐标的定义&#xff0c;基于固定分辨率的图片&#xff0c;通过获取该图片x和y坐标确定位置后并添加标注&#xff0c;实现位置展示、对应图片内物品展示的一种标注开发方式。 技术要点 自动获取图片x和y坐标&#xff1b;将多个坐标xy在图片上通过CSS定位的方式予以展示&am…
阅读更多...
pytorch学习（三）——模型层

pytorch学习（三）——模型层

文章目录1. 自定义模型层2. 使用预训练模型3. 模型构建风格3.1 使用 add_module 方法3.2 添加进 Sequential3.3 Sequential作为模型容器3.4 ModuleList作为模型容器3.5 ModuleDict作为模型容器当我们构建了数据管道能够将数据一个batch一个batch的取出来后&#xff0c;下一步就…
阅读更多...
微信小程序函数处理之保姆级讲解

微信小程序函数处理之保姆级讲解

目录 生命周期函数 生命周期函数的调用过程 页面事件函数 页面路由管理 自定义函数 setData设值函数 生命周期函数 在使用Page&#xff08;&#xff09;构造器注册页面时&#xff0c;需要使用生命周期函数&#xff0c;包括onLoad&#xff08;&#xff09;页面加载时生命周…
阅读更多...
硬件工程师成长之路（10.1）——芯片选型

硬件工程师成长之路（10.1）——芯片选型

系列文章目录 1.元件基础 2.电路设计 3.PCB设计 4.元件焊接 5.板子调试 6.程序设计 7.算法学习 8.编写exe 9.检测标准 10.项目举例 11.职业规划 文章目录前言一、电机驱动类1 、直流电机驱动芯片2、步进电机③、资料前言 送给大学毕业后找不到奋斗方向的你&#xff08;每周…
阅读更多...
【车间调度】基于全球邻域和爬坡来优化模糊柔性作业车间调度问题（Matlab代码实现）

【车间调度】基于全球邻域和爬坡来优化模糊柔性作业车间调度问题（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️❤️&#x1f4a5;&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑…
阅读更多...
VS Studio 搭建跨平台开发环境

VS Studio 搭建跨平台开发环境

VS Studio 搭建跨平台开发环境 增加VS的工作负载 打开Visual Studio Installer 安装器&#xff0c;点击修改 在这个界面找到Linux开发环境&#xff0c;勾上然后在点击右下角的修改等待安装。我的是因为已经有了所以下面那里显示的是关闭&#xff0c;没有的是显示的修改 等待安…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023