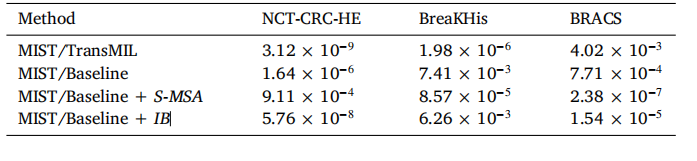
这是结果

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define _CRT_SECURE_NO_WARNINGS

// 定义边表结点结构
typedef struct EdgeNode {
    int adjvex;  // 邻接顶点域，存储该边所指向的顶点
    struct EdgeNode* next;  // 指向下一条边的指针
} EdgeNode;

// 定义顶点表结点结构
typedef struct VertexNode {
    int data;  // 顶点域，存储顶点信息
    EdgeNode* firstEdge;  // 指向邻接表的第一个边表结点
} VertexNode;

// 定义图结构
typedef struct {
    VertexNode adjList[100];  // 顶点数组
    int numVertices, numEdges;  // 顶点数和边数
} GraphAdjList;



// 队列结构，用于广度优先遍历
typedef struct {
    int data[100];  // 存储顶点索引
    int front, rear;
} Queue;

// 初始化队列
void initQueue(Queue* q) {
    q->front = q->rear = 0;
}

// 判断队列是否为空
bool isEmpty(Queue* q) {
    return q->front == q->rear;
}

// 入队
void enqueue(Queue* q, int vertex) {
    q->data[q->rear++] = vertex;
}

// 出队
int dequeue(Queue* q) {
    return q->data[q->front++];
}

// 广度优先遍历（BFS）
void BFS(GraphAdjList G, int startVertex) {
    bool visited[100] = { false };  // 访问标记数组
    Queue q;
    initQueue(&q);  // 初始化队列

    printf("BFS Traversal: ");

    visited[startVertex] = true;  // 标记起始顶点已访问
    printf("%d ", G.adjList[startVertex].data);
    enqueue(&q, startVertex);  // 起始顶点入队

    while (!isEmpty(&q)) {
        int v = dequeue(&q);  // 出队当前顶点
        EdgeNode* e = G.adjList[v].firstEdge;  // 获取该顶点的邻接表

        // 遍历所有邻接节点
        while (e) {
            if (!visited[e->adjvex]) {  // 如果邻接顶点未被访问
                printf("%d ", G.adjList[e->adjvex].data);
                visited[e->adjvex] = true;  // 标记已访问
                enqueue(&q, e->adjvex);  // 邻接顶点入队
            }
            e = e->next;
        }
    }

    printf("\n");
}

// 深度优先遍历的递归函数
void DFSUtil(GraphAdjList G, int v, bool visited[]) {
    visited[v] = true;  // 标记该顶点已访问
    printf("%d ", G.adjList[v].data);  // 输出顶点

    EdgeNode* e = G.adjList[v].firstEdge;  // 获取该顶点的邻接表

    // 遍历所有邻接节点
    while (e) {
        if (!visited[e->adjvex]) {  // 如果邻接顶点未被访问
            DFSUtil(G, e->adjvex, visited);  // 递归访问邻接顶点
        }
        e = e->next;
    }
}

// 深度优先遍历（DFS）
void DFS(GraphAdjList G, int startVertex) {
    bool visited[100] = { false };  // 访问标记数组
    printf("DFS Traversal: ");
    DFSUtil(G, startVertex, visited);  // 从起始顶点开始递归遍历
    printf("\n");
}

// 创建图
void createGraph(GraphAdjList* G) {
    int i, j, k;
    EdgeNode* e;

    // 输入顶点数和边数
    printf("输入顶点数和边数: ");
    scanf_s("%d %d", &G->numVertices, &G->numEdges);

    // 输入顶点信息
    for (i = 0; i < G->numVertices; i++) {
        printf("输入顶点 %d 的信息: ", i + 1);
        scanf_s("%d", &G->adjList[i].data);
        G->adjList[i].firstEdge = NULL;  // 初始化顶点的边表指针为空
    }

    // 输入边信息，构建邻接表
    for (k = 0; k < G->numEdges; k++) {
        printf("输入边 (vi, vj) 的顶点下标 i 和 j: ");
        scanf_s("%d %d", &i, &j);

        // 头插法插入结点 (vi -> vj)
        e = (EdgeNode*)malloc(sizeof(EdgeNode));  // 创建边结点
        e->adjvex = j;  // 邻接顶点为 j
        e->next = G->adjList[i].firstEdge;  // 将新结点插入顶点 i 的边表
        G->adjList[i].firstEdge = e;

        // 无向图需要插入另一条边 (vj -> vi)
        e = (EdgeNode*)malloc(sizeof(EdgeNode));  // 创建边结点
        e->adjvex = i;  // 邻接顶点为 i
        e->next = G->adjList[j].firstEdge;  // 将新结点插入顶点 j 的边表
        G->adjList[j].firstEdge = e;
    }
}
int main() {
    GraphAdjList G;

    // 创建图 (这里假设图的输入方式与之前一致)
    createGraph(&G);  // 根据你的图结构输入顶点和边的信息

    // 执行广度优先遍历，从顶点 0 开始
    BFS(G, 0);

    // 执行深度优先遍历，从顶点 0 开始
    DFS(G, 0);

    return 0;
}