1 完善程序
最大子矩阵和
给出 m行 n列的整数矩阵,求最大的子矩阵和(子矩阵不能为空)。
输入第一行包含两个整数 m和 n,即矩阵的行数和列数。之后 m行,每行 n个整数,描述整个矩阵。程序最终输出最大的子矩阵和。
(最后一空 4 分,其余 3分,共 16 分)
比如在如下这个矩阵中:
4 4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
拥有最大和的子矩阵为:
9 2
-4 1
-1 8
其和为 15
3 3
-2 10 20
-1 100 -2
0 -2 -3
最大子矩阵和为 128
4 4
0 -2 -9 -9
-9 11 5 7
-4 -3 -7 -6
-1 7 7 5
最大子矩阵和为 26
#include <iostream>
using namespace std;
const int SIZE = 100;
int matrix[SIZE + 1][SIZE + 1];
int rowsum[SIZE + 1][SIZE + 1]; /* rowsum[i][j]记录第i行前j个数的和 */
int m, n, i, j, first, last, area, ans;
int main()
{
cin >> m >> n;
for ( i = 1; i <= m; i++ )
for ( j = 1; j <= n; j++ )
cin >> matrix[i][j];
ans = matrix ①;
for ( i = 1; i <= m; i++ )
②;
for ( i = 1; i <= m; i++ )
for ( j = 1; j <= n; j++ )
rowsum[i][j] = ③;
for ( first = 1; first <= n; first++ )
for ( last = first; last <= n; last++ )
{
④;
for ( i = 1; i <= m; i++ )
{
area += ⑤;
if ( area > ans )
ans = area;
if ( area < 0 )
area = 0;
}
}
cout << ans << endl;
return(0);
}
1 ①处应填( )
2 ②处应填( )
3 ③处应填( )
4 ④处应填( )
5 ⑤处应填( )
2 相关知识点
1) 前缀和
前缀和(Prefix Sum)是一种常见的算法技巧,用于快速计算数组中某个区间内元素的和。它的基本思想是将数组元素依次累加,形成一个前缀和数组,通过前缀和数组可以快速计算任意区间的元素和
示例
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和
第1行,分别为n,m
第2行,长度为n的序列
接下来m行,每行分别对应l和r
5 3
2 1 3 6 4
1 2
1 3
2 4
输出分析
1 2 输出3 - 2+1=3
1 3 输出6 - 2+1+3=6
2 4 输出10 - 1+3+6=10
源程序
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N];//存放读入数据数组
int s[N];//前缀和数组
int main() {
int n,m;
int l,r;
scanf("%d %d",&n,&m);
for(int i = 1;i<=n;i++){
scanf("%d",&a[i]);
s[i] += s[i-1] + a[i];//预处理前缀和
}
for(int i = 1;i<=m;i++){
scanf("%d %d",&l,&r);
printf("%d\n",s[r] - s[l-1]);//通过前缀和公式直接访问
}
system("pause");
return 0;
}
/*
输入
5 3
2 1 3 6 4
1 2
1 3
2 4
输出
3
6
10
*/
2) 矩阵
矩阵(matrix)是数学中的一个矩形数组,由行和列构成,表示一组数值、变量或表达式。矩阵在多种学科中有广泛应用,包括线性代数、物理、计算机科学、统计学等
例如
假设有一个 3×3的矩阵
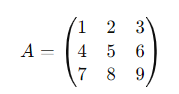
3) 子矩阵
在上面3×3的矩阵中,如果我们删除第 2 行和第 2 列,得到的子矩阵为

3 思路分析
1 计算每一行对应列的前缀和
for ( i = 1; i <= m; i++ )
for ( j = 1; j <= n; j++ )
rowsum[i][j] = rowsum[i] [j-1]+matrix[i] [j];
2 遍历二维数组任意2列,锁定每一个子矩阵
for ( first = 1; first <= n; first++ )
for ( last = first; last <= n; last++ )
{
3 计算每一个子矩阵的和,计算思路为
加入当前行,计算一个新的子矩阵,如果此矩阵之和大于0,则和之前最大矩阵打擂台
如果此矩阵之和小于0,则说明前面这些对后面无矩阵和无帮助,重新开始计算矩阵和
for ( i = 1; i <= m; i++ )
{
area += rowsum[i] [last]-rowsum[i] [first-1];
if ( area > ans )
ans = area;
if ( area < 0 )
area = 0;
}
1 ①处应填( [1] [1] )
分析
初始矩阵第一个数,这个数也是一个子矩阵,后续如果有更大的,可以通过打擂台的方式替换调
2 ②处应填( rowsum[i] [0]=0 )
分析
真实数据从第1列开始,每行的第0列初始为0,后续计算矩阵和时,可以通用使用前一列+当前列
3 ③处应填( rowsum[i] [j-1]+matrix[i] [j] )
分析
每行计算前缀和,rowsum[i][j]表示,第i行,前j列的和
rowsum[i][j]=rowsum[i] [j-1]+matrix[i] [j]
表示第i行,前j列的和=第i行,前j-1列的和+第1行,第1列的数
4 ④处应填( area=0 )
分析
通过下面双重循环,固定列后,计算这些列之间m行的最大子矩阵的和累加到area变量中
每增加一行,如果是正的数,和最终结果ans打擂台
如果是负数,下一行重新开始累加计算
for ( first = 1; first <= n; first++ )
for ( last = first; last <= n; last++ )
{
5 ⑤处应填( rowsum[i] [last]-rowsum[i] [first-1] )
分析
根据前缀和,某一行从first到last之间和,可以通过当前行的last列-(first-1)获取,避免循环累加计算