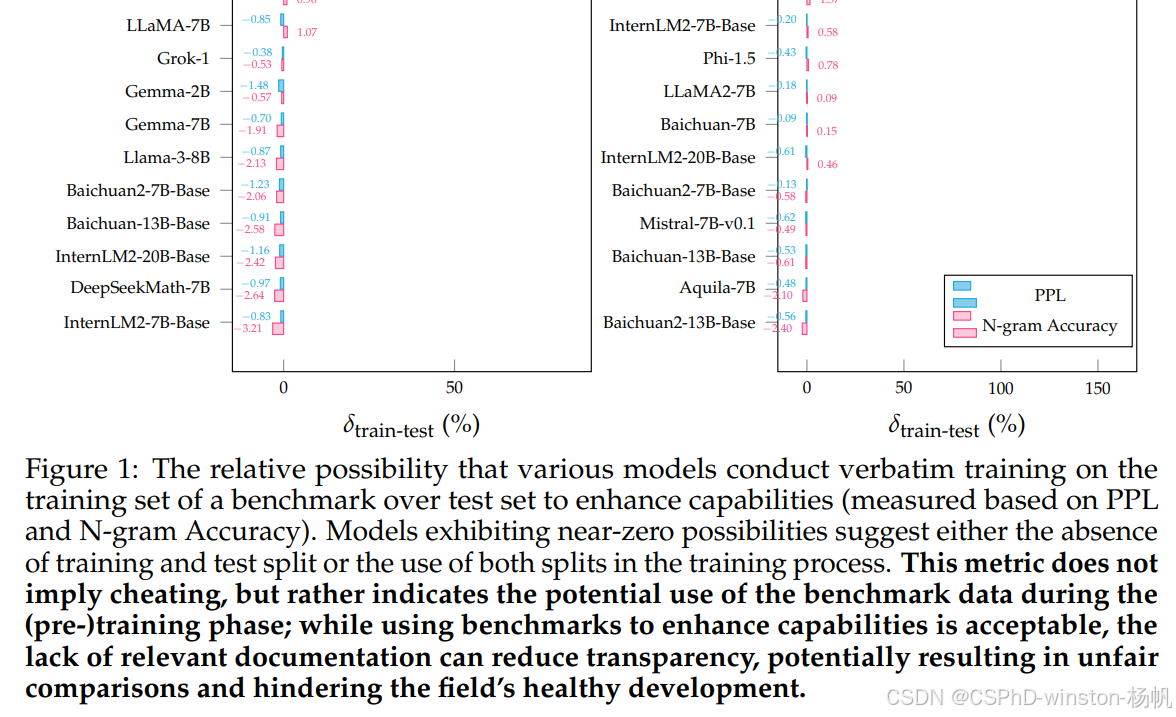
累计分布函数（CDF）在统计学上是一个由0增长到1的曲线。5G中CDF被3GPP标准推荐使用，5G 天线阵的有效全向辐射功率EIRP的CDF函数被用来评价设备的质量和性能。由于EIRP是在某一个方向角theta, phi上的辐射功率，幅值由天线增益与激励功率乘积决定，所以EIRP在球形全方向上有最大值和最小值，且区间内连续。所以，我们可定义一个概率函数，表示EIRP在一定值内的概率，该概率函数自然就有累计分布函数CDF。
CDF在EIRP最小值以下为零，EIRP最大值以上为1。所以CDF是以EIRP为横坐标变量的增长函数，该函数展示了EIRP在球形全方向的分布。
虽然CDF=0时的EIRP才是能达到球形辐射状态的最小的EIRP值，考虑实际环境限制和损耗，3GPP标准实际则要求CDF=0.5时的EIRP，比如要达到至少11.5dBm。
CDF=1 时，对应的EIRP就是该天线阵能达到的EIRP峰值，3GPP标准也要求这个EIRP峰值要高过一个最小值。比如智能手机毫米波段这个最小值在20-22dBm左右，其他类别毫米波段设备的最小值可以是29dBm,43dBm等；当然EIRP峰值也有要低于一个最大值，比如智能手机毫米波段最大值为43dBm。
当然对于不同设备，标准还可以定义CDF=0.2，0.6 或0.8时的EIRP值，都有一定的范围要求。在设备后期仿真过程中，加上人体模型或外界环境的仿真，天线辐射区域有所遮挡，EIRP下降，CDF是会整体左移的。如果设计不当，比如CDF=0.5时的EIRP本身不够高，虽然可以加大激励信号功率，使CDF曲线整体右移，但是要冒着总辐射功率（TRP）超标的风险。
这里我们以一个简化的毫米波封装天线AIP为例，演示如何获取CDF。
STEP1 仿真得到全S参数
天线S参数显示工作频段为n257的26.5GHz-29.5GHz毫米波。
单端口的远场显示均匀主瓣向上。
Step2 定义激励参数：每个端口的振幅和相位，控制振幅或相位的theta和phi
后处理“2Dand 3D Field Results -> - Combine Results using am-ph Parameters”, 点击ok, 参数列表处会自动生成振幅和相位参数，默认振幅“am”为1，相位“ph“为0，这步只需要运行一次，如果用CST的Array Task, 则参数定义都自动化。
此外，这个后处理还生成一个新的远场结果，后缀为[comb-am-ph]，这个远场只有一个EIRP波束，我们需要多个EIRP波束的扫描结果来算总体的CDF。
这里我们可以看到一个定向的远场波束。
在扫描之前，可以根据天线数字信号的激励信息修改这些参数。这里我们用180*sinD(theta)和不同系数来控制端口2，3，4的相位。如果有激励列表，我们也可以支持导入。
Step3 定义后处理Total Scan Pattern (TSP)
扫描之前，还需要定义后处理扫描全图。这里选择Realized Gain。
后处理参数扫描theta或phi 得到TSP。下面进行参数扫描，注意这里用的是后处理扫描，不重新进行三维激励运算。这里扫描是要记录下哪个方向上的远场信息，我们用简单五个theta角度。
如果用户有自己的扫描点，可以通过这里的Import导入。扫描之后得到总扫描波束，如下图所示：
关于如何生成Total Scan方向图，也可以参考下面两篇过去的文章FAQ 008 如何仿真Total Scan方向图的和FAQ 010 如何仿真Total Scan方向图(2)。
Step4 定义和运行后处理CDF
最后定义一个远场后处理，选择TSP，RealizedGain，还有CDF。
Evaluate单独运行这个CDF后处理即可。
CDF结果在Tables里面，如下图所示：
调整一下坐标。这里我们横坐标用的是RealizedGain，单位是dB,转化成EIRP还需加上激励功率，用后处理将x轴加上输入功率，比如10dBm。
横坐标调整后，我们便得到了CDF。这时结果还在Tables里面，横坐标名称还没有改。用户可将这个结果重新拷贝到1DResult 新建文件夹，然后右键曲线属性修改名称，比如EIRP等。
本案例只在三维界面中用增益获取CDF。当然还有其他方法获得CDF，比如在schematic里通过后处理，或者通过powerflow功率密度推导，都可以反复验证CDF的准确性。
【推荐内容】
Abaqus从入门到精通（1）Abaqus的主要模块和文件类型www.think-s.com/CAE?article_id=1474
https://link.zhihu.com/?target=https%3A//www.think-s.com/CAE%3Farticle_id%3D1474
Abaqus从入门到精通（2）Abaqus的使用环境www.think-s.com/CAE?article_id=1475https://link.zhihu.com/?target=https%3A//www.think-s.com/CAE%3Farticle_id%3D1475
Abaqus从入门到精通（3）Abaqus 2022新功能www.think-s.com/CAE?article_id=1476https://link.zhihu.com/?target=https%3A//www.think-s.com/CAE%3Farticle_id%3D1476
