文章目录
- 1. ImageNet
- 2. 卷积计算
- 2.1 两个多项式卷积
- 2.2 函数卷积
- 2.3 循环卷积
- 3. 周期循环矩阵和非周期循环矩阵
- 4. 循环卷积特征值
- 4.1 卷积计算的分解
- 4.2 运算量
- 4.3 二维卷积公式
- 5. Kronecker Product
1. ImageNet
ImageNet 的论文paper链接如下:详细请直接阅读相关论文即可
通过网盘分享的文件:imagenet_cvpr09.pdf
链接: https://pan.baidu.com/s/1Rkb6S5RbCHZUBrgUCIv0FA?pwd=6ffn 提取码: 6ffn
- 涉及到的知识点:
– drop-out–防止神经网络过拟合
– 正则化-- 方便数据训练
2. 卷积计算
2.1 两个多项式卷积
教授讲得通用公式听起来糊里糊涂的,就以简单的实际案例来解释吧!
假设我们有两个多项式表示如下:
P
(
x
)
=
1
+
2
x
+
3
x
2
;
Q
(
x
)
=
4
+
5
x
;
H
(
x
)
=
P
(
x
)
Q
(
x
)
\begin{equation} P(x)=1+2x+3x^2;Q(x)=4+5x;H(x)=P(x)Q(x) \end{equation}
P(x)=1+2x+3x2;Q(x)=4+5x;H(x)=P(x)Q(x)
- 两个多项式相乘后展开可得结果如下:
P ( x ) = 1 + 2 x + 3 x 2 ; Q ( x ) = 4 + 5 x ; H ( x ) = P ( x ) Q ( x ) \begin{equation} P(x)=1+2x+3x^2;Q(x)=4+5x;H(x)=P(x)Q(x) \end{equation} P(x)=1+2x+3x2;Q(x)=4+5x;H(x)=P(x)Q(x)
H ( x ) = 4 + 13 x + 22 x 2 + 15 x 3 \begin{equation} H(x)=4+13x+22x^2+15x^3 \end{equation} H(x)=4+13x+22x2+15x3 - 那么我们是否可以根据卷积的形式直接算出来了?
P ( x ) : p = [ 1 , 2 , 3 ] , Q ( x ) : q = [ 4 , 5 , 0 ] \begin{equation} P(x):p=[1,2,3],Q(x):q=[4,5,0] \end{equation} P(x):p=[1,2,3],Q(x):q=[4,5,0] - 那么两个序列卷积如下 ,可得,
多项式的乘积等同于其系数的卷积,多项式乘法可以看作是序列卷积的一个具体应用

2.2 函数卷积
函数卷积定义:若
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x)有界且可积,以为函数卷积连续形式如下:
K
(
x
)
=
f
(
x
)
∗
g
(
x
)
=
∫
−
∞
+
∞
f
(
t
)
g
(
x
−
t
)
d
t
\begin{equation} K(x)=f(x)*g(x)=\int_{-\infty}^{+\infty}f(t)g(x-t)\mathrm{dt} \end{equation}
K(x)=f(x)∗g(x)=∫−∞+∞f(t)g(x−t)dt
2.3 循环卷积
具体参考上节笔记
线性代数|机器学习-P32循环矩阵的特征向量-傅里叶矩阵
3. 周期循环矩阵和非周期循环矩阵
- Toeplitz Matrix :
对于非周期循环矩阵来说,我们用托普利兹矩阵Toeplitz Matrix 表示,主要特点为斜对角值相等,但不循环 - Circulant Matrix;
对于周期循环矩阵来说,我们用循环矩阵Circulant Matrix 表示,主要特点为斜对角值相等,并且元素循环,也是循环卷积矩阵,根据上节课学习可得,任意一个循环卷积矩阵C都可以是位移矩阵P的线性组合,并且矩阵P的特征向量为傅里叶矩阵。

- 周期循环矩阵C的特征向量为傅里叶矩阵,以4阶举例可得:
C = c 0 + c 1 P + c 2 P 2 + c 3 P 3 , P = [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] ; F 4 = [ 1 1 1 1 1 i i 2 i 3 1 i 2 i 4 i 6 1 i 3 i 6 i 9 ] \begin{equation} C=c_0+c_1P+c_2P^2+c_3P^3, P=\begin{bmatrix} 0&1&0&0\\\\ 0&0&1&0\\\\ 0&0&0&1\\\\ 1&0&0&0\end{bmatrix};F_4=\begin{bmatrix} 1&1&1&1\\\\ 1&i&i^2&i^3\\\\ 1&i^2&i^4&i^6\\\\ 1&i^3&i^6&i^9\end{bmatrix} \end{equation} C=c0+c1P+c2P2+c3P3,P= 0001100001000010 ;F4= 11111ii2i31i2i4i61i3i6i9 - 循环矩阵C的特征值可以用傅里叶F表示:

4. 循环卷积特征值
4.1 卷积计算的分解

- 我们定义矩阵如下:
C = [ c 0 c 1 c 1 c 0 ] ; D = [ d 0 d 1 d 1 d 0 ] ; F = [ 1 1 1 − 1 ] \begin{equation} C=\begin{bmatrix} c_0&c_1\\\\ c_1&c_0 \end{bmatrix};D=\begin{bmatrix} d_0&d_1\\\\ d_1&d_0 \end{bmatrix};F=\begin{bmatrix} 1&1\\\\ 1&-1 \end{bmatrix} \end{equation} C= c0c1c1c0 ;D= d0d1d1d0 ;F= 111−1
F c = [ c 0 + c 1 c 0 − c 1 ] ; F d = [ d 0 + d 1 d 0 − d 1 ] ; \begin{equation} Fc=\begin{bmatrix} c_0+c_1\\\\ c_0-c_1 \end{bmatrix};Fd=\begin{bmatrix} d_0+d_1\\\\ d_0-d_1 \end{bmatrix};\end{equation} Fc= c0+c1c0−c1 ;Fd= d0+d1d0−d1 ;
( F c ) . ∗ ( F d ) = [ ( c 0 + c 1 ) ( d 0 + d 1 ) ( c 0 − c 1 ) ( d 0 − d 1 ) ] = [ c 0 d 0 + c 0 d 1 + c 1 d 0 + c 1 d 1 c 0 d 0 − c 0 d 1 − c 1 d 0 + c 1 d 1 ] ; \begin{equation} (Fc).* (Fd)=\begin{bmatrix} (c_0+c_1)(d_0+d_1)\\\\ (c_0-c_1)(d_0-d_1) \end{bmatrix}=\begin{bmatrix} c_0d_0+c_0d_1+c_1d_0+c_1d_1\\\\ c_0d_0-c_0d_1-c_1d_0+c_1d_1 \end{bmatrix};\end{equation} (Fc).∗(Fd)= (c0+c1)(d0+d1)(c0−c1)(d0−d1) = c0d0+c0d1+c1d0+c1d1c0d0−c0d1−c1d0+c1d1 ;
c ⊗ d = [ c 0 c 1 c 1 c 0 ] [ d 0 d 1 ] = [ c 0 d 0 + c 1 d 1 c 1 d 0 + c 0 d 1 ] ; \begin{equation} c\otimes d=\begin{bmatrix} c_0&c_1\\\\c_1&c_0 \end{bmatrix}\begin{bmatrix} d_0\\\\d_1 \end{bmatrix}=\begin{bmatrix} c_0d_0+c_1d_1\\\\c_1d_0+c_0d_1 \end{bmatrix};\end{equation} c⊗d= c0c1c1c0 d0d1 = c0d0+c1d1c1d0+c0d1 ;
F ( c ⊗ d ) = [ 1 1 1 − 1 ] [ c 0 d 0 + c 1 d 1 c 1 d 0 + c 0 d 1 ] = [ c 0 d 0 + c 1 d 1 + c 1 d 0 + c 0 d 1 c 0 d 0 + c 1 d 1 − c 1 d 0 − c 0 d 1 ] ; \begin{equation} F(c\otimes d)=\begin{bmatrix} 1&1\\\\1&-1 \end{bmatrix}\begin{bmatrix} c_0d_0+c_1d_1\\\\c_1d_0+c_0d_1 \end{bmatrix}=\begin{bmatrix} c_0d_0+c_1d_1+c_1d_0+c_0d_1\\\\c_0d_0+c_1d_1-c_1d_0-c_0d_1 \end{bmatrix};\end{equation} F(c⊗d)= 111−1 c0d0+c1d1c1d0+c0d1 = c0d0+c1d1+c1d0+c0d1c0d0+c1d1−c1d0−c0d1 ; - 小结卷积规则如下:

4.2 运算量
因为我们知道傅里叶变换中有一个大名鼎鼎的快速傅里叶变换的算法FFT,其运算复杂度为 N log N N\log N NlogN
- 方式一:对于先卷积后傅里叶变换的计算量如下:
F ( c ⊗ d ) = N 2 + N log N \begin{equation} F(c\otimes d)=N^2+N\log N\end{equation} F(c⊗d)=N2+NlogN - 方式二:先进行傅里叶变换后在点积的计算量如下:
( F c ) . ∗ ( F d ) = 2 N log N + N \begin{equation} (Fc).* (Fd)=2N\log N+N\end{equation} (Fc).∗(Fd)=2NlogN+N - 当N=1024时,可得:
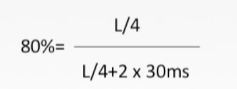
F ( c ⊗ d ) ( F c ) . ∗ ( F d ) = 1024 + 10 2 ∗ 10 + 1 = 49.238 \begin{equation} \frac{F(c\otimes d)}{(Fc).* (Fd)}=\frac{1024+10}{2*10+1}=49.238\end{equation} (Fc).∗(Fd)F(c⊗d)=2∗10+11024+10=49.238 - 简单来说,对于同样的卷积计算来说,我们选择方式二,如果把数列先进行傅里叶变换,再将序列点乘,得到的计算量在N=1024情况下,方式一的计算量居然是方式二的接近50倍。简直令人发指!!!所以我们需要拥抱FFT快速傅里叶变换,将数据的处理换一种方式进行,这样可以大大提高程序运行的速度!!!真是伟大的傅里叶!!!
4.3 二维卷积公式
假设我们有两个函数
f
(
x
,
y
)
,
g
(
x
,
y
)
f(x,y),g(x,y)
f(x,y),g(x,y),它们的二维卷积公式如下:
h
(
x
,
y
)
=
f
(
x
,
y
)
∗
g
(
x
,
y
)
=
∫
∞
∫
∞
f
(
u
,
v
)
g
(
x
−
u
,
y
−
v
)
d
u
d
v
\begin{equation} h(x,y)=f(x,y)*g(x,y)=\int^{\infty}\int^{\infty}f(u,v)g(x-u,y-v)\mathrm{du}\mathrm{dv}\end{equation}
h(x,y)=f(x,y)∗g(x,y)=∫∞∫∞f(u,v)g(x−u,y−v)dudv
5. Kronecker Product
- Kronecker Product 介绍:

- 举例介绍:
A = [ 1 2 3 4 ] ; B = [ 0 5 6 7 ] \begin{equation} A=\begin{bmatrix}1&2\\\\3&4\end{bmatrix};B=\begin{bmatrix}0&5\\\\6&7\end{bmatrix}\end{equation} A= 1324 ;B= 0657
A ⊗ B = [ 1 ⋅ B 2 ⋅ B 3 ⋅ B 4 ⋅ B ] = [ 0 5 0 10 6 7 12 14 0 15 0 20 18 21 24 28 ] \begin{equation} A\otimes B=\begin{bmatrix}1\cdot B&2\cdot B\\\\3\cdot B&4\cdot B\end{bmatrix}= \begin{bmatrix} 0&5&0&10\\\\ 6&7&12&14\\\\ 0&15&0&20\\\\ 18&21&24&28 \end{bmatrix}\end{equation} A⊗B= 1⋅B3⋅B2⋅B4⋅B = 0601857152101202410142028