声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~

今天给大家介绍一种非常小众的智能优化算法应用，这个应用非常容易理解而且新颖小众。目前，知网和WOS上也几乎没有类似的文献，非常适合作为创新点，让审稿人眼前一亮，也能够检验一个优化算法的性能好坏。

以往论文中通常用工程应用来证明一个算法在实际工程中的好坏，但实际上这些工程应用也仅仅是一些带约束的优化问题，已经被彻底用烂了，不光是中文核心，很多SCI也是重灾区，审稿人也早已看腻。

因此，我们本期要介绍的一个应用是三维TSP问题，并且，利用2024年的最新优化算法——北极海鹦优化算法APO进行求解，且调用的算法均为大家常用的算法格式，学会这一篇，大家可自行替换成自己想要的算法。

TSP问题，也就是旅行商问题，属于路径规划类一个非常经典的问题之一，它指的是给定一组城市和城市之间的距离，要求找出一个最短的路线，使得旅行商从一个城市出发，经过每个城市一次后返回起点。TSP属于NP难问题。随着城市数量的增加，解的数量呈指数级增长，如果靠死算，甚至要以年为单位来计算时间。因此，TSP问题非常适合利用智能优化算法进行求解，也能判断一个算法的性能好坏。

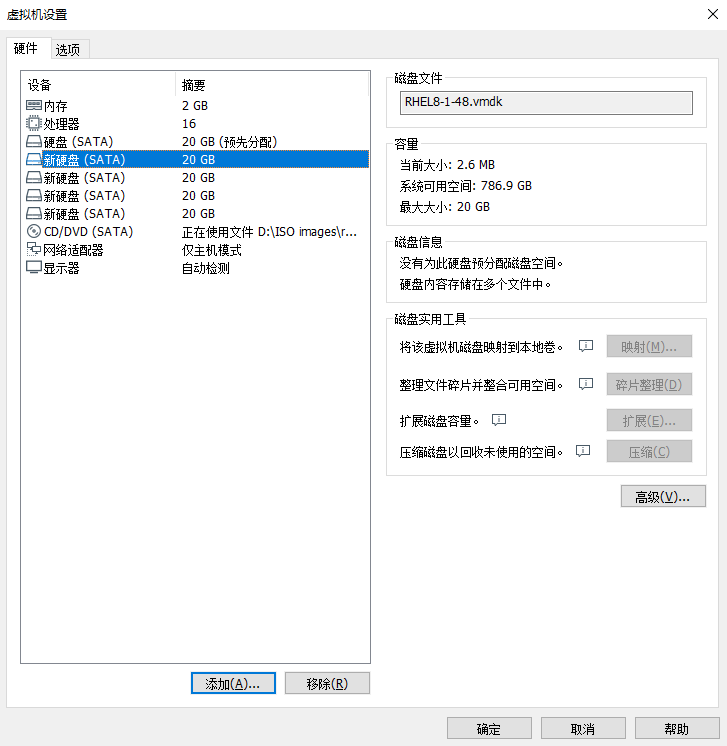
传统的TSP问题都是二维，也就是只有x和y两个坐标。三维TSP问题则加入了z坐标，也就是三个坐标。大家在输入数据的时候非常简单，只需在txt文件内输入一行的三个坐标即可：

从左到右分别是x坐标、y坐标、z坐标。同时，设置种群数量为100，最大迭代为5000（均可自行修改），利用大家所熟知的优化算法函数格式输入，如下所示：

load('data.txt')             % 导入TSP数据集
N = 100;                     % 种群数量（可以修改）
Max_iteration = 5000;        % 最大迭代次数（可以修改）
dim = size(data,1)-1;        % 维度
lb = -100;                   % 下界
ub = 100;                    % 上界
fobj = @Fun;                 % 目标函数
[Best_Pos,Best_fit,curve]=APO(N,Max_iteration,lb,ub,dim,fobj);

得到的结果如下所示：

第一张图是三维路径图，相比于二维路径图更具挑战性、也更美观，整个路径空间以三维方式呈现，大家也可自由拖动其中的路径，更直观的展现路径优化结果。

第二张图是APO的收敛曲线图，这个算法性能也是非常不错，在CEC2017上取得过很好的效果，之前也做过一期推文：

2024年9月SCI新算法-北极海鹦优化算法(APO)-公式原理详解与性能测评 Matlab代码免费获取

由收敛曲线图可知，大概5000次时已经接近收敛，同时，控制台也会输出每次迭代的数值以及最优路线结果：

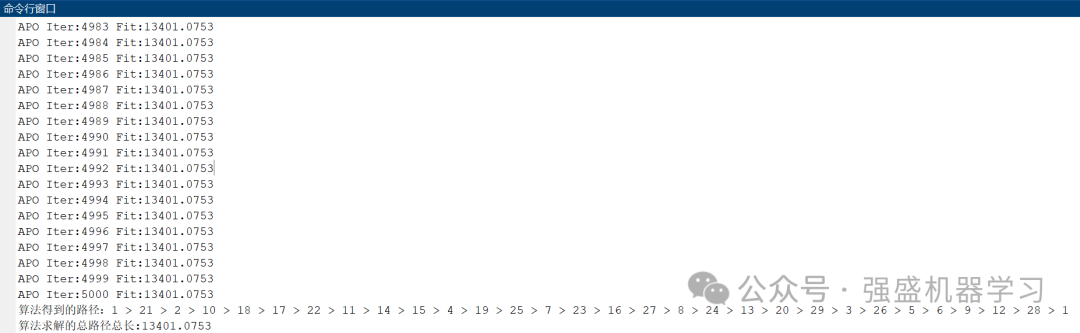
为了方便大家写作，这边也给出此应用的数学模型（很容易理解）：

TSP问题的目标非常简单，就是找到一条经过每个城市一次的最短路线，最后回到出发城市，用公式可以表示为：

其中，𝑎𝑏为使用路线城市𝑎到城市𝑏的决策变量。另外，𝑐𝑎𝑏表示城市𝑎到城市𝑏的距离，同时𝑐𝑎𝑏> 0。目标函数是总行程最短，第一个约束确保通过求解优化问题所提供的解中不包含子行程；第二个约束确保列表中的每个城市只从一个城市到达；第三个约束则保证每个城市与另一个城市之间的距离和距离都只有一个。对于三维TSP问题，坐标从二维变成了三维，整体模型架构并没有改变。

以上所有图片，一键运行main即可全部出图，非常清晰，适合新手小白。

想要以上Matlab代码的，可以点击下方小卡片，再后台回复关键词，不区分大小写：

SWTSP